A ring of radius R having uniformly distributed charge Q. is mounted on a rod suspended by two identical strings. The tension in strings in equilibrium is T0. Now, a vertical magnetic field is switched on and ring is rotated at constant angular velocity co. Find the maximum value of co h which the ring can be rotated if the strings can withstand a maximum tension of 3T02
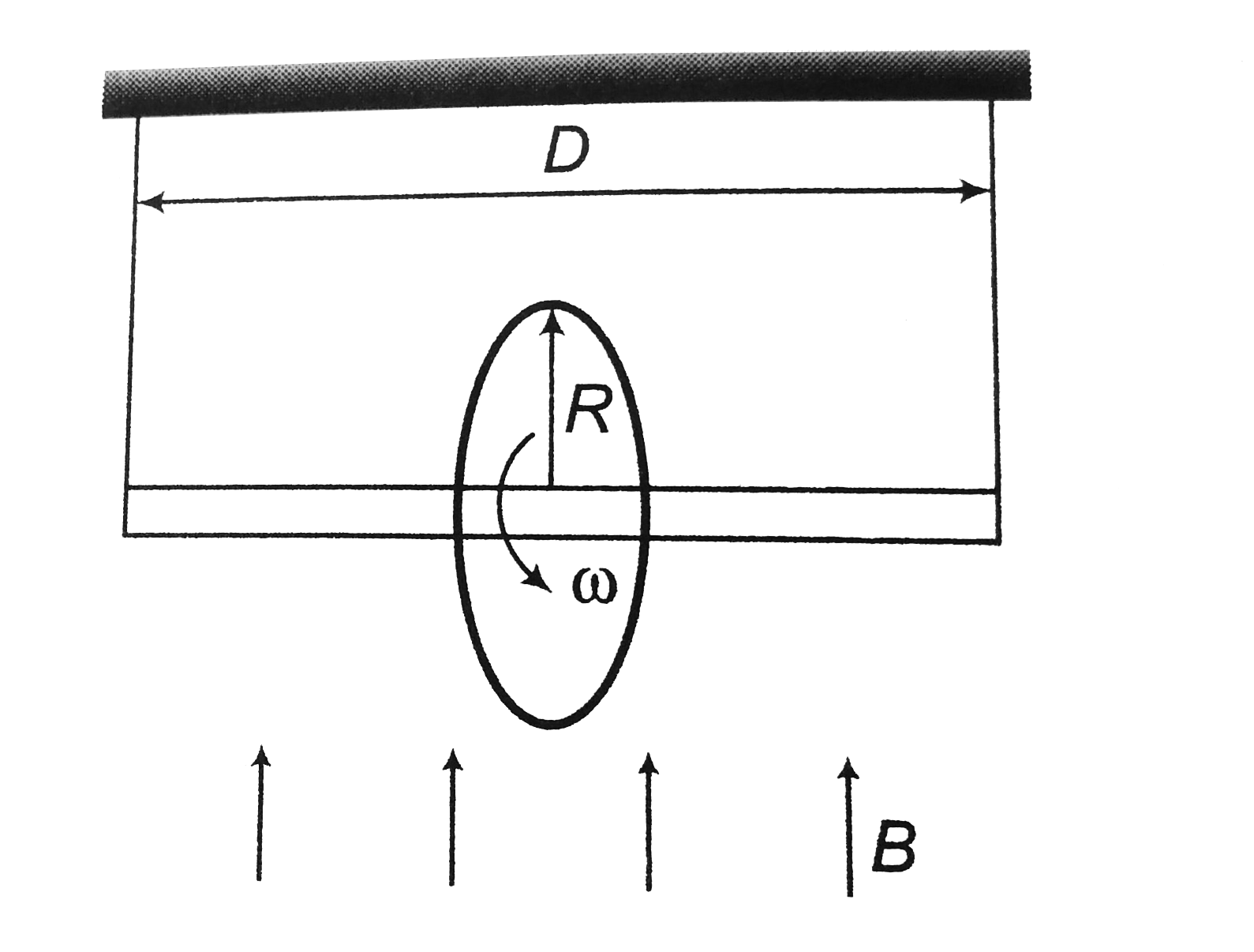
In equilibrium,
2T0=mg
or T0=mg2….(i)
magnetic moment, M=iA=(ω2πQ)(πR2)
τ=MBsin90∘=ωBQR22
Let T1andT2 be the tensions in the two strings when magnetic
field is switched on (T1>T2)
For translation equilibrium,
T1+T2=mg....(ii)
For rotational equilibrium
(T1−T2)D2=τ=ωBQR22
or T1−T2=ωBQR2D....(iii)
Solving Eqs. (ii) and (iii) we have
T1=mg2+ωBQR22D
As T1>T2 and maximum values of T1 can be 3T0/2, we have
3T02=T0+ωmaxBQR22D(mg2=T0)
∴ωmax=DT0BQR2
Topper's Solved these Questions
- MAGNETIC FIELD AND MAGNETIC FORCESBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - MAGNETIC FIELD AND MAGNETIC FORCESEXERCISE - Exercise 1.1
22 Videos
- MAGNETIC FIELD AND MAGNETIC FORCESBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - MAGNETIC FIELD AND MAGNETIC FORCESEXERCISE - Exercise 1.2
13 Videos
- MAGNETIC FIELD AND MAGNETIC FORCESBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - MAGNETIC FIELD AND MAGNETIC FORCESEXERCISE - Multiple Correct Answer type
2 Videos
- INDUCTANCEBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - INDUCTANCEEXERCISE - Concept Based
8 Videos
- MISCELLANEOUS VOLUME 3BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - MISCELLANEOUS VOLUME 3EXERCISE - True and False
3 Videos
Similar Questions
A ring of radius R having unifromly distributed charge Q is mounted on a rod suspended by two identical strings. The tension in strings in equilibrium is T0. Now a vertical magnetic field is switched on and ring is rotated at constant angular velocity ω. Find the maximum ω with which the ring can be rotated if the strings can withstand a maximum tension of 3T0/2.

View SolutionThe breaking tension of a string is 10 N. A particle of mass 0.1 kg tied to it is rotated along a horizontal circle of radius 0.5 meter. The maximum speed with which the particle can be rotated without breaking the string is
View SolutionA stone of mass 0.3 kg tied to the end of a string in a horizontal plane in whirled round in a circle of radius 1 m withp. speed of 40 rev/min. What is the tension in the string ? What is the maximum speed with which the stone can be whirled around if the string can withstand a maximum tension of 200 N ?
View SolutionA stone of of mass 0.25 kg tied to the end of a string is whirled round in a circle of radius 1.5 m with a speed of 40rev/min in a horizontal plane What is the tension in the string ? What is the maximum speed with which the stone can be whirled around If the string can withstand a maximum tension of 200 N ?
View SolutionA ring of mass m, radius r having charge q uniformly distributed over it and free to rotate about its own axis is placed in a region having a magnetic field B parallel to its axis. If the magnetic field is suddenly switched off, the angular velocity acquired by the ring is:
View SolutionA conducting ring of radius r having charge q is rotating with angular velocity ω about its axes. Find the magnetic field at the centre of the ring.

View SolutionA conducting ring of radius r having charge q is rotating with angular velocity ω about its axes. Find the magnetic field at the centre of the ring.

View SolutionA ring of mass m and radius R is given a charge q. It is then rotated about its axis with angular velocity ω.Find
(ii) Magnetic field produced at the centre of ring.
View SolutionA stone of mass 0.5 kg is attached to a string of length 2 m and is whirled in a horizontal circle. If the string can with stand a tension of 9N, the maximum velocity with which the stone can be whirled is:
View SolutionA non - conducting ring of mass m = 4 kg and radius R = 10 cm has charge Q = 2 C uniformly distributed over its circumference. The ring is placed on a rough horizontal surface such that the plane of the ring is parallel to the surface. A vertical magnetic field B=4t3T is switched on at t = 0. At t = 5 s ring starts to rotate about the vertical axis through the centre. The coefficient of friction between the ring and the surface is found to be k24. Then the value of k is
View Solution
