A slightly divergent beam of charged particles accelerated by a Potential difference V propogates from a point A along the axis of a solenoid. The beam is brought into focus at a distance l from the point A at two successive values of magnetic induction B1andB2. Find the specific charge q/m of the particles.
To find the specific charge qm of the charged particles in the given scenario, we will follow these steps:
Step 1: Understand the Motion of Charged Particles in a Magnetic Field
When a charged particle moves in a magnetic field, it experiences a magnetic force that causes it to move in a helical path if it has a component of velocity parallel to the magnetic field. The velocity can be broken down into two components: one parallel to the magnetic field (vcosθ) and one perpendicular to it (vsinθ).
Step 2: Determine the Pitch of the Helical Path
The pitch p of the helix can be expressed as:
p=vcosθ⋅T
where T is the time period for one complete revolution in the magnetic field, given by:
T=2πmqB
Thus, substituting for T:
p=vcosθ⋅2πmqB
Step 3: Relate the Length Moved to the Pitch
If the beam focuses at a distance l after completing n revolutions, the total distance moved can be expressed as:
l=n⋅p=n⋅(vcosθ⋅2πmqB)
Step 4: Analyze for Two Magnetic Inductions
When the beam is focused at two different magnetic inductions B1 and B2, we can write two equations:
1. For B1:
l=2πmvcosθqB1
2. For B2:
l=2πmvcosθqB2
Step 5: Set Up the Equations
From the above equations, we can express B1 and B2:
B1=2πmvcosθlq
B2=2πmvcosθlq
Step 6: Find the Difference
Subtract the two equations:
B2−B1=2πmvcosθlq(1B2−1B1)
Step 7: Express the Velocity
The kinetic energy gained by the charged particle due to the potential difference V is given by:
12mv2=qV⟹v=√2qVm
Step 8: Substitute and Solve for qm
Substituting v into the difference equation and rearranging gives:
qm=8π2V(B2−B1)2
Final Result
Thus, the specific charge qm of the particles is:
qm=8π2V(B2−B1)2
When a charged particle moves in a magnetic field, it experiences a magnetic force that causes it to move in a helical path if it has a component of velocity parallel to the magnetic field. The velocity can be broken down into two components: one parallel to the magnetic field (vcosθ) and one perpendicular to it (vsinθ).
The pitch p of the helix can be expressed as:
p=vcosθ⋅T
where T is the time period for one complete revolution in the magnetic field, given by:
T=2πmqB
Thus, substituting for T:
p=vcosθ⋅2πmqB
If the beam focuses at a distance l after completing n revolutions, the total distance moved can be expressed as:
l=n⋅p=n⋅(vcosθ⋅2πmqB)
When the beam is focused at two different magnetic inductions B1 and B2, we can write two equations:
1. For B1:
l=2πmvcosθqB1
2. For B2:
l=2πmvcosθqB2
From the above equations, we can express B1 and B2:
B1=2πmvcosθlq
B2=2πmvcosθlq
Subtract the two equations:
B2−B1=2πmvcosθlq(1B2−1B1)
The kinetic energy gained by the charged particle due to the potential difference V is given by:
12mv2=qV⟹v=√2qVm
Substituting v into the difference equation and rearranging gives:
qm=8π2V(B2−B1)2
Thus, the specific charge qm of the particles is:
qm=8π2V(B2−B1)2
Topper's Solved these Questions
- MAGNETIC FIELD AND MAGNETIC FORCESBook:CENGAGE PHYSICS ENGLISHChapter:MAGNETIC FIELD AND MAGNETIC FORCESExercise:Exercise 1.1
Explore 22 Videos
- MAGNETIC FIELD AND MAGNETIC FORCESBook:CENGAGE PHYSICS ENGLISHChapter:MAGNETIC FIELD AND MAGNETIC FORCESExercise:Exercise 1.2
Explore 13 Videos
- MAGNETIC FIELD AND MAGNETIC FORCESBook:CENGAGE PHYSICS ENGLISHChapter:MAGNETIC FIELD AND MAGNETIC FORCESExercise:Multiple Correct Answer type
Explore 2 Videos
- INDUCTANCEBook:CENGAGE PHYSICS ENGLISHChapter:INDUCTANCEExercise:Concept Based
Explore 8 Videos
- MISCELLANEOUS VOLUME 3Book:CENGAGE PHYSICS ENGLISHChapter:MISCELLANEOUS VOLUME 3Exercise:True and False
Explore 3 Videos
Similar Questions
A particle of charges Q and mass m travels through a potential difference V from rest. The final momentum of the particle is
View SolutionThe kinetc energy of a chargd particle decreased by 10 J as it moves from a point at potential 100 V to a point at potential 200V . Find the charge on the particle.
View Solution
Knowledge Check
A particle starts from point A moves along a straight line path with an acceleration given by a = p - qx where p, q are connected and x is distance from point A . The particle stops at point B. The maximum velocity of the particle is
ApqBp√qCqpD√qp
A charged particle, having charge q1 accelerated through a potential difference V enters a perpendicular magnetic field in which it experiences a force F. It V is increased to 5V, the particle will experience a force
View SolutionA particle of mass m carrying charge q is accelerated by a potential difference V. It enters perpendicularly in a region of uniform magnetic field B and executes circular arc of radius R, then qm equals
View SolutionA positively charged particle, having charge q, is accelerated by a potential difference V. This particle moving along the x-axis enters a region where an electric field E exists. The direction of the electric field is along positive y-axis. The electric field exists in the region bounded by the lines x=0andx=a. Beyond the line x=a (i.e., in the region x>a), there exists a magnetic field of strength B, directed along the positive y-axis. Find

a. at which point does the particle meet the line x=a.
b. the pitch of the helix formed after the particle enters the region x≥a. (Mass of the particle is m.)
View SolutionA particle of mass m and charge q is accelerated by a potential difference V volt and made to enter a magnetic field region at an angle θ with the field. At the same moment, another particle of same mass and charge is projected in the direction of the field from the same point. Magnetic field induction is B. What would be the speed of second particle so that both particles meet again and again after regular interval of time. Also, find the time interval after which they meet and the distance travelled by the second particle during that interval.
View SolutionA particle of mass m and charge q is accelerated by a potential difference V volt and made to enter a magnetic field region at an angle θ with the field. At the same moment, another particle of same mass and charge is projected in the direction of the field from the same point. Magnetic field induction is B. What would be the speed of second particle so that both particles meet again and again after regular interval of time. Also, find the time interval after which they meet and the distance travelled by the second particle during that interval.
View SolutionTwo point charges, each of mass m and charge q are released when they are at a distance d from each other. What is the speed of each charged particle when they are at a distance 2r ?
View Solution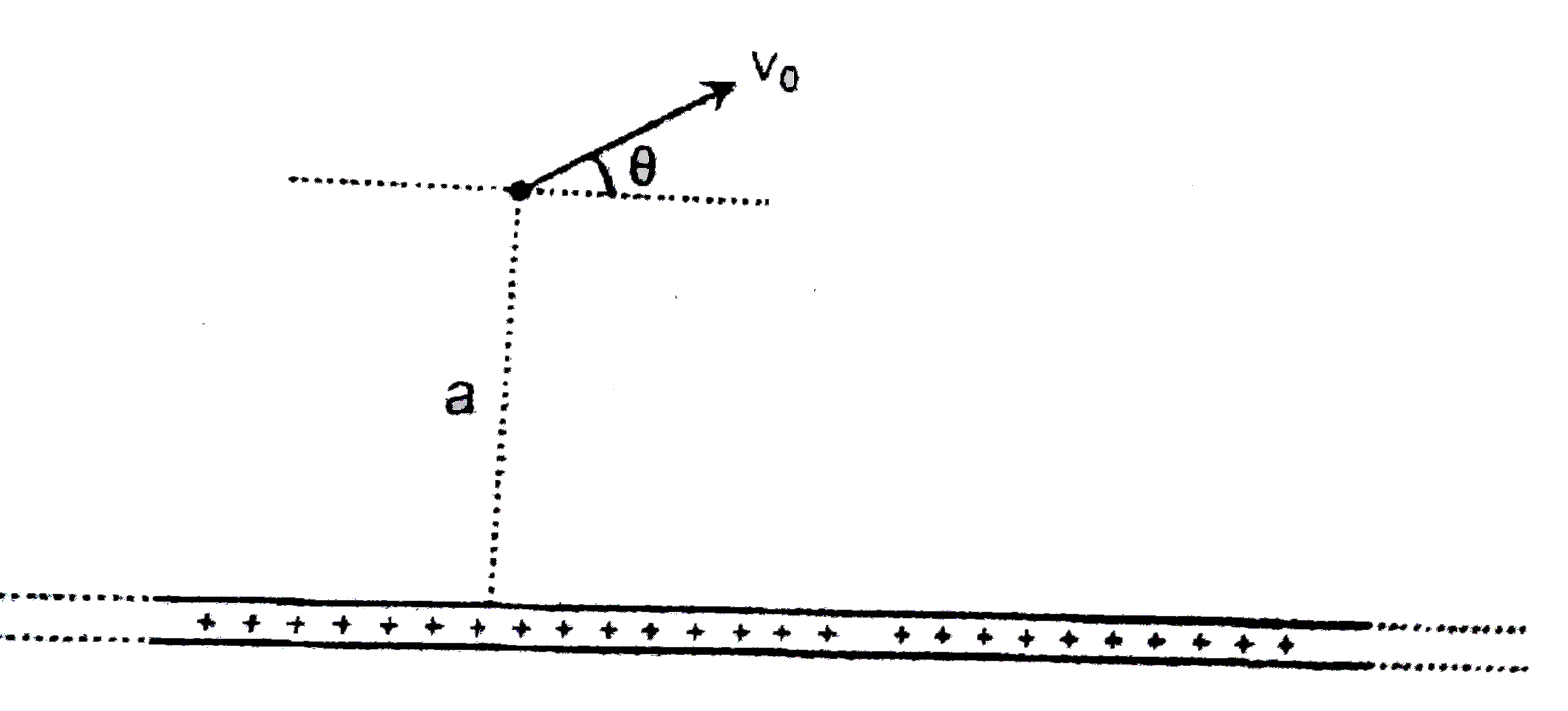
There is an infinite line of uniform linear density of charge +λ. A particle of charge −q & mass m is projected with initial velocity v0 at an angle θ with the line of charge from a distance a from it. The point charge moves in plane containing line charge and point of projection The speed of the particle of found to be minimum when it's distance from the line of charge is ae(nπmε20/qλ). The value of n is (ingnore gravity)
View Solution