An electron in the ground state of hydrogen atom is removing in unanticlockwise direction in a circle orbit of radius $R$

a. Obtain an expression for the orbital magnetic dipole moment of the electron .
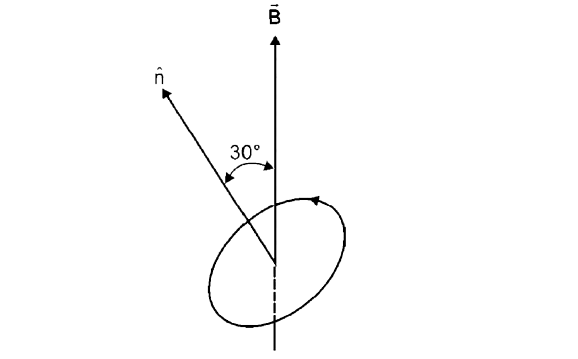
b. The atom is placed in a uniform magnetic indution $¯ ¯ ¯ B$ such that the plane normal to the electron orbitmakes an angle of $30^{\circ}$ with the magnetic induction. Find the tarque experienced by the orbiting electron .

Video Solution

Text Solution

Verified by Experts

(a) In ground state $(n = 1)$ according to Bohr's theory:
$m v R = \frac{h}{2 π} or v = \frac{h}{2 π m R}$
Now time peroid, $T = \frac{2 π R}{v} = \frac{2 π R}{h / 2 π m R} = \frac{4 π^{2} m R^{2}}{h}$
Magnetic moment $M = i A$
where $I = \frac{charge}{time period} = \frac{e}{\frac{4 π^{2} m R^{2}}{h}} = \frac{e h}{4 π^{2} m R^{2}}$
and $A = π R^{2}$
$∴ M = (π R^{2}) (\frac{e h}{4 π^{2} m R^{2}}) or M = \frac{e h}{4 π m}$
Direction of magnetic moment $\to M$ is perpendicular to the
plane of orbit.
(b) $\to τ = \to M \times \to B$
$| \to τ | = M B sin θ$
where $θ$ is the angle between $\to M and \to B θ = 30^{\circ}$
$∴ τ = (\frac{e h}{4 π m}) (B) {sin 30}^{\circ} = \frac{e h B}{8 π m}$
The direction of $\to τ$ is perpendicular to both $\to M and \to B$ .

Updated on:21/07/2023

An electron in the ground state of hydrogen atom is revolving in anticlockwise direction in circular orbit of radius R. The orbital magnetic dipole moment of the electron will be
A $\frac{e h}{4 π m}$
B $\frac{e h}{2 π m}$
C $\frac{e h^{2}}{4 π m}$
D $\frac{e^{2} h}{4 π m}$
An electron moving in a circular orbit of radius r makes n rotations per second per second. The magnetic moment of the orbital electron is
Azero
B $π r^{2} n e$
C $π r^{2} n^{2} e$
D $\frac{r^{2} n e}{2 π}$