A proton of mass 1.67×10−27 kg and charge 1.6×10−19C is shot a uniform magnetic field, and perpendicular to the field with a velocity 5×106m/s. If the magnetic induction of the field is 1 tesla, find
(i) The radius of the circular path
To find the radius of the circular path of a proton moving in a magnetic field, we can use the formula for the radius r of the circular motion of a charged particle in a magnetic field, which is given by:
r=mvqB
Where:
- m is the mass of the proton,
- v is the velocity of the proton,
- q is the charge of the proton,
- B is the magnetic field induction.
1. Identify the given values:
- Mass of the proton, m=1.67×10−27kg
- Charge of the proton, q=1.6×10−19C
- Velocity of the proton, v=5×106m/s
- Magnetic field induction, B=1T
2. Substitute the values into the formula:
r=(1.67×10−27kg)×(5×106m/s)(1.6×10−19C)×(1T)
3. Calculate the numerator:
Numerator=1.67×10−27×5×106=8.35×10−21kg m/s
4. Calculate the denominator:
Denominator=1.6×10−19×1=1.6×10−19C T
5. Divide the numerator by the denominator to find the radius:
r=8.35×10−211.6×10−19=5.21875×10−2m
6. Round the result:
r≈5.22×10−2m
Final Answer:
The radius of the circular path is approximately 5.22×10−2m or 0.0522m.
---
- m is the mass of the proton,
- v is the velocity of the proton,
- q is the charge of the proton,
- B is the magnetic field induction.
- Mass of the proton, m=1.67×10−27kg
- Charge of the proton, q=1.6×10−19C
- Velocity of the proton, v=5×106m/s
- Magnetic field induction, B=1T
r=(1.67×10−27kg)×(5×106m/s)(1.6×10−19C)×(1T)
Numerator=1.67×10−27×5×106=8.35×10−21kg m/s
Denominator=1.6×10−19×1=1.6×10−19C T
r=8.35×10−211.6×10−19=5.21875×10−2m
r≈5.22×10−2m
The radius of the circular path is approximately 5.22×10−2m or 0.0522m.
Topper's Solved these Questions
- MOVING CHARGES & MAGNETISM Book:VMC MODULES ENGLISHChapter:MOVING CHARGES & MAGNETISM Exercise:SOLVED EXAMPLES
Explore 20 Videos
- MOVING CHARGES & MAGNETISM Book:VMC MODULES ENGLISHChapter:MOVING CHARGES & MAGNETISM Exercise:PRACTICE EXERCISE 1
Explore 1 Video
- MOVING CHARGES & MAGNETISM Book:VMC MODULES ENGLISHChapter:MOVING CHARGES & MAGNETISM Exercise:IMPECCABLE
Explore 53 Videos
- Motion in Two DimensionsBook:VMC MODULES ENGLISHChapter:Motion in Two DimensionsExercise:MCQ
Explore 2 Videos
- PROPERTIES OF MATTERBook:VMC MODULES ENGLISHChapter:PROPERTIES OF MATTERExercise:JEE Advanced (Archive) Level - 2 (MATRIX MATCH TYPE)
Explore 1 Video
Similar Questions
A proton of mass 1.67×10−27 kg and charge 1.6×10−19C is shot a uniform magnetic field, and perpendicular to the field with a velocity 5×106m/s. If the magnetic induction of the field is 1 tesla, find
(ii) The frequency of revolution.
View SolutionA particle of mass 1.6×10−27kg and charge 1.6×10−19 coulomb enters a uniform magnetic field of 1 Tesla as shown in the figure. The speed of the particle is 107m/s. The distance PQ will be
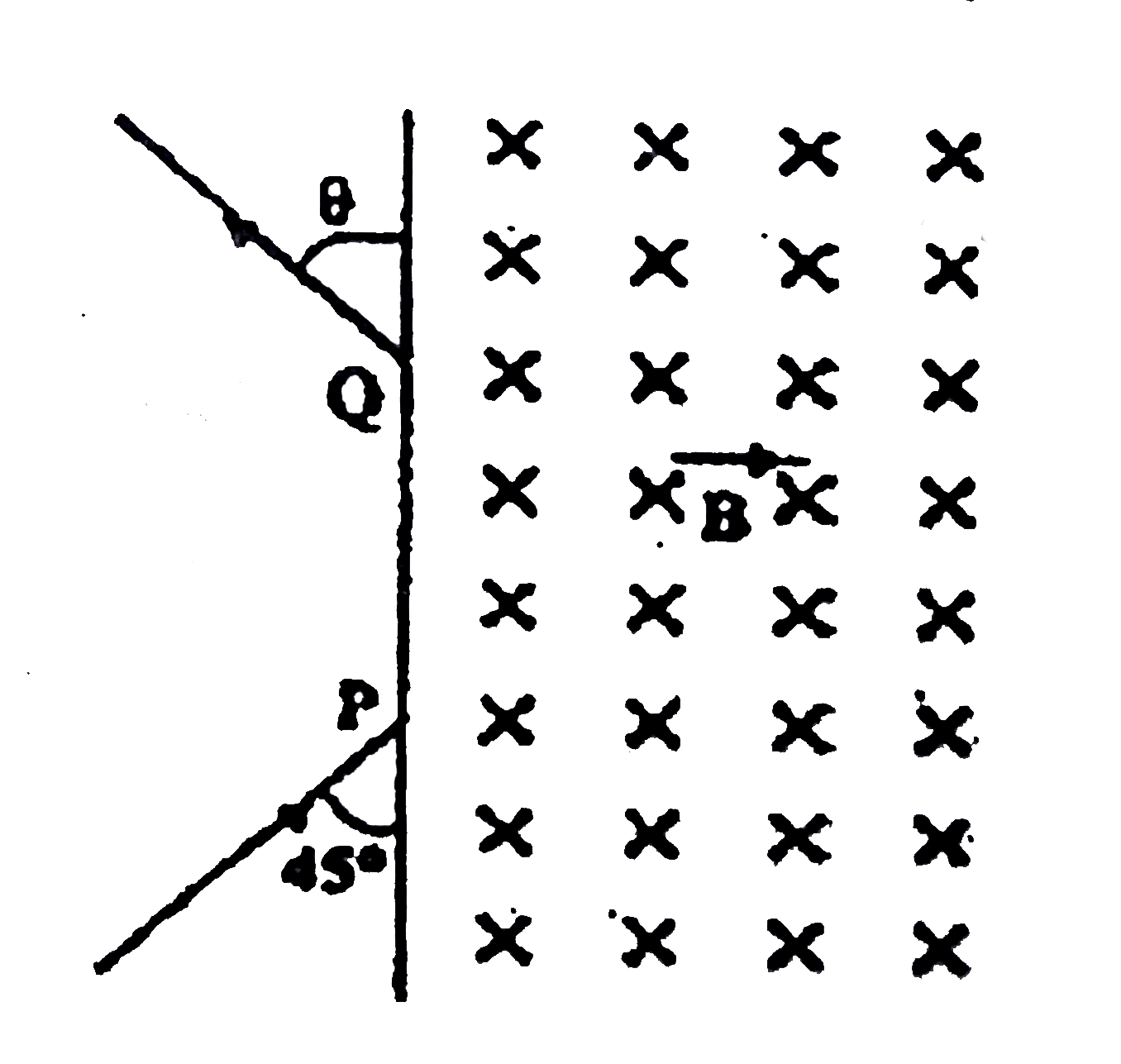
View SolutionA particle of mass m=1.6×10−27 kg and charge q=1.6×10−19C enters a region of uniform magnetic field of stregth 1T along the direction shown in figure. The speed of the particle is 107m/s

a. The magnetic field is directed along the inward normal to the plane of the paper. The particle leaves the region of the fiedl at the point F. Find the distasnce EF and the angle theta.
b. If the direction of the field is along the outward normal to the plane of the paper find the time spent by the particle in the regin of the magnetic field after entering it at E.
View SolutionA proton of mass 1.67×10−27 kg charge 1.6×10−19C is projected in xy-plane with a speed of 2×106m/s at an angle of 60∘ to the X-axis. If a uniform magnetic field of 0.14 T is applies along the Y-axis, then the path of the proton is
View SolutionA proton of mass 1.66×10−27kg is moving with kinetic energy 5×10−27J .What is the wavelength of proton ?
View SolutionA proton has a mass 1.67 ×10−27 kg and charge +1.6×10−19C. If the proton is accelerated through a potential difference of million volts, then the kinetic energy is
View SolutionA particle of mass m=1.6X10−27 kg and charge q=1.6X10−19 C moves at a speed of 1.0X107ms−7. It enters a region of uniform magnetic field at a point E, as shown in The field has a strength of 1.0 T. (a) The magnetic field is directed into the plane of the paper. The particle leaves the region of the filed at the point F. Find the distance EF and the angle theta. (b) If the field is coming out of the paper, find the time spent by the particle in the regio the magnetic feld after entering it at E.

View SolutionIn an orbit of radius 0.5A0 an electron revolves with a frequency of 6.25×1015 Hz. The magnetic induction field at its centre is
View SolutionAnswer the following:
a) Obtain the expression for the deflecting torque acting on the current carrying rectangular coil of a Galvanometer in a uniform magnetic field. Why is a radial magnetic field employed in the moving coil galvanometer?
b) Particles of mass 1.6×10−27 kg and charge 1.6×10−19 C are accelerated in a cyclotron of dee radius 40 cm. It employs a magnetic field of 0.4T. Find the kinetic energy (in MeV) of the particle beam imparted by the accelerator.
View SolutionA beam of ions with velocity 2×105 m/s enters normally into a uniform magnetic field of 4×10−2 T. if the specific charge to the ions is 5×107 C/kg, the radius of the circular path described will be
View Solution