In the arrangement shown in Fig., slits S1 and S4are having a variable separation Z. Point O on the screen is at the common perpendicular bisector of S1S2 and S3S4.
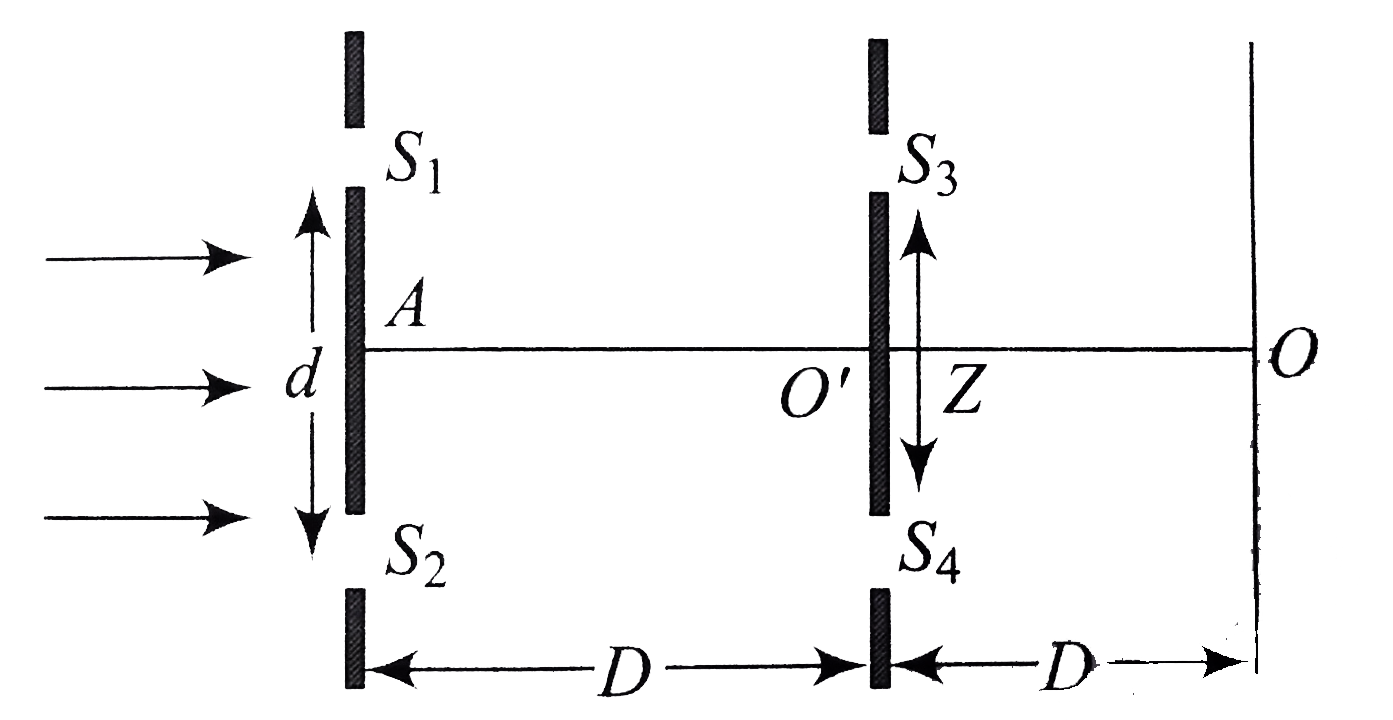
If a hole is made at O' on AO' O and the slit S4 is closed, then the ratio of the maximum to minimum observed on screen at O , if O'S3 is equal to λD4d, is
1
infinity
34
4
The correct Answer is:c
Intensity at S3=A20+A20+2A20cosϕ
where ϕ=2πβλD4d=2πdλD×λD4d=π2
Is3=A20(2+2cos(π2))
=2A20×cos2(π4)=42A20=2A20
Amplitude of wave at S3,A3=√2A0
Maximum intensity at O' =(A0+√2A0)2
Maximum intensity at O =(√2A0−A0)2
ImaxImin=(√2+1√2−1)2=(√2+1)4=34
Topper's Solved these Questions
- WAVE OPTICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - WAVE OPTICSEXERCISE - Integer
3 Videos
- WAVE OPTICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - WAVE OPTICSEXERCISE - Archives
4 Videos
- WAVE OPTICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - WAVE OPTICSEXERCISE - Assertion- Reasoning
13 Videos
- SOURCES OF MAGNETIC FIELDBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - SOURCES OF MAGNETIC FIELDEXERCISE - single correct Ansewer type
12 Videos
Similar Questions
In the arrangement shown in Fig., slits S1 and S4are having a variable separation Z. Point O on the screen is at the common perpendicular bisector of S1S2 and S3S4.
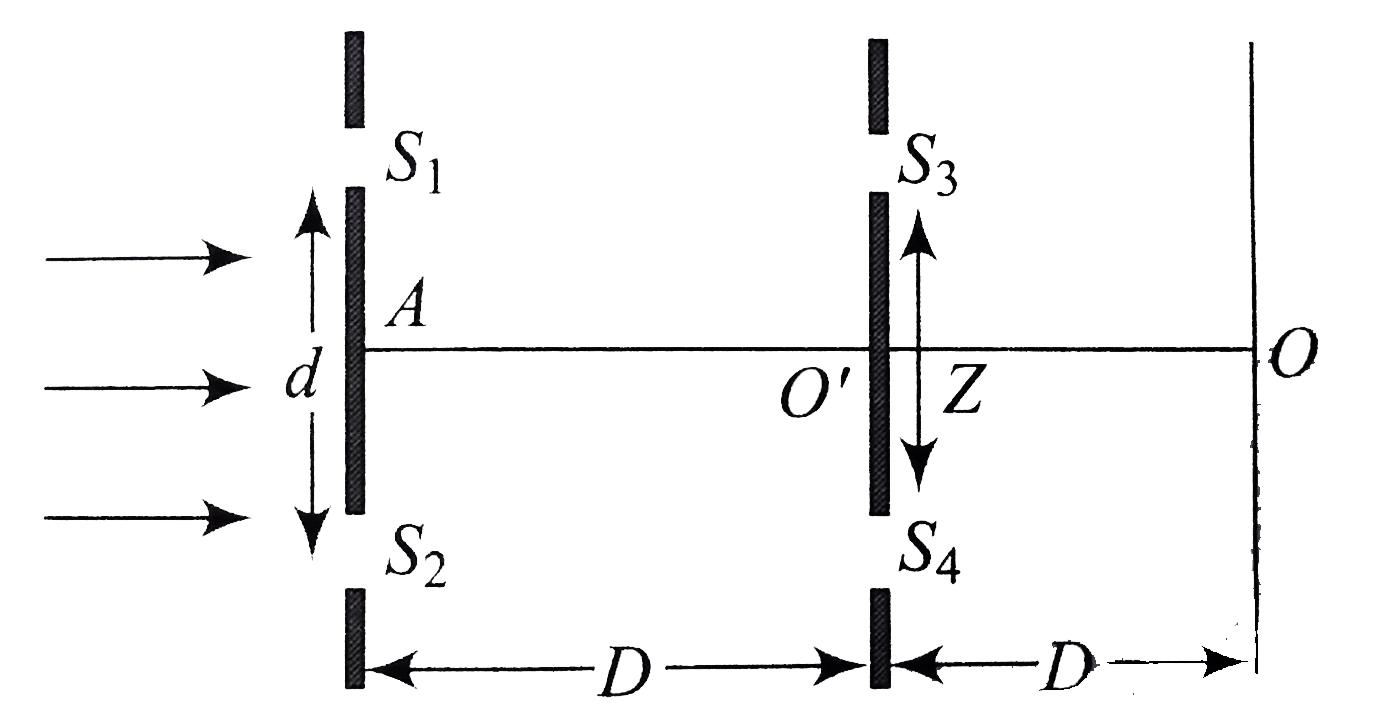
The minimum value of Z for which the intensity at O is zero is
View SolutionIn the arrangement shown in Fig., slits S1 and S4are having a variable separation Z. Point O on the screen is at the common perpendicular bisector of S1S2 and S3S4.

When Z=λD2d, the intensity measured at O is I0. The intensity at O When Z=2λDd is
View SolutionIn arrangement shown in figure, plane wavefront of monochromatic light of wavelength λ is incident on identical slits S1 and S2. There is another pair of indentical slits S3 and S4 which are having separation Z=λD2d Point O is on the screen at the common perpendicular bisector of S1S2 and S3S4.I1 is the intensity at point O Now the board having slits S3S4 is moved upward parallel to itself and perpendicular to line AO till slit S4 is on line AO and it is observed that now intensity at point O is I2 then I2I1 is :

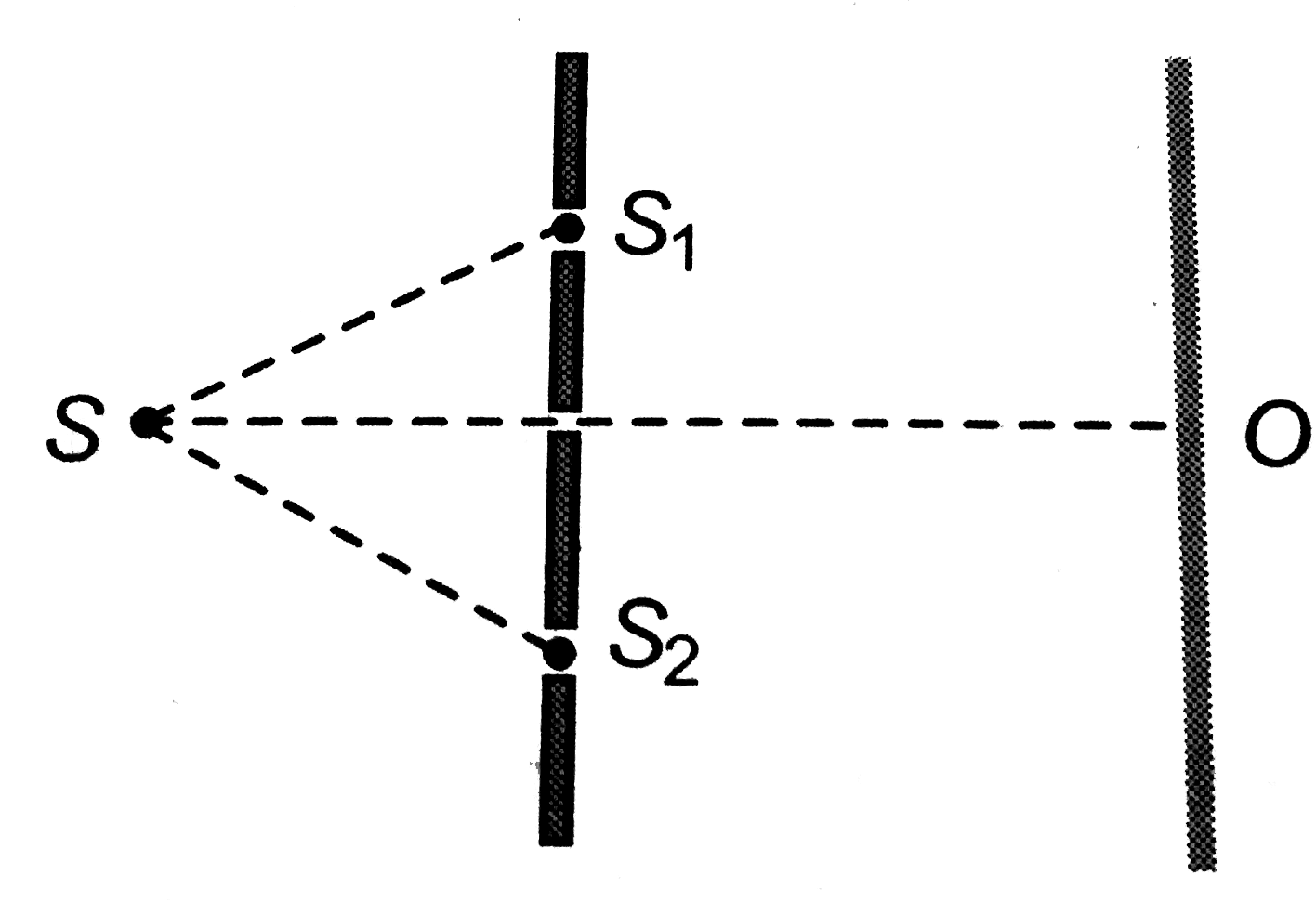
View SolutionIn the set up shown in figure, the two slits S1 and S2 are not equidistant from the slit S. The central fringe at O is then
View SolutionConsider the arrangement shown in figure. By some mechanism,
the separation between the slits S3andS4 can be changed. The intensity is
measured at the point P which is at the common perpendicular bisector of S1S2
and S3S4. When z=Dλ2d, the intensity measured at P is I. Find the intensity when
z is equal to

(a)Dλd(b)3Dλ2d(c)2Dλd .
View SolutionIn the arrangement shown in figure, z1 and z2 are two screens. Line PO is the bisector line of s1s2 and s3s4,s1 is removed, resultant intensity at O due to slits s1 and s2 is l. now z1 is placed. For different values of y given in column-I match the resultant intensity at O given in column -II.

View SolutionConsider the situation shown in figure. The two slits S1andS2 placed symmetrically around the central line are illuminated by a monochromatic light of wavelength λ. The separation between the slits is d. The light transmitted by the slits falls on a screen Σ1 placed at a distance D from the slits. The slit S3 is at the placed central line and the slit S4, is at a distance z from S3. Another screenΣ2 is placed a further distance D away from 1,1. Find the ratio of the maximum to minimum intensity observed on Σ2 if z is equal to a. z=λD2d b. λDd c. λD4d

View Solution_S01_026_Q01.png)
In a YDSE experiment two slits S1 and S2 have separation of d=2mm the distance of the screen is D=85 m source S starts moving from a very large distance towards S2 perpendicular to S1S2 as shown in figure the wavelength of monochromatic light is 500 nm. The number of maximas observed on the screen at point P as the moves towards S2 is
View SolutionS2O2−8 have
View SolutionDraw structure H2S2O4
View Solution
