When light from two sources (say slits S1 and S2) interfere, they form alternate dark and bright fringes. Bright fringe is formed at all point where the path difference is an odd multiple of half wavelength. At the condition of equal amplitudes, A1=A2=a, the maximum intensity will be 4a2 and the visibility improves, The resultant intensity can also be indicated with phase factor as I=2a2cos2(ϕ/2).Using this passage, answer the following questions.
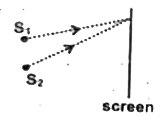
If the slits S1 and S2 are arranged as shown in Fig. the ratio of intensity of fringe at P and R is

0
∞
1:1
1:2
The correct Answer is:a
Since the ligth from slit S1 and S2 reach the point P with a path difference of λ/2, the point P will be dark, I=0. Since path difference is zero for R, there will be a bright fringe at R. So, ratio of intensity will be zero. So choice (a) is correct.
Topper's Solved these Questions
- WAVE OPTICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - WAVE OPTICSEXERCISE - Integer
3 Videos
- WAVE OPTICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - WAVE OPTICSEXERCISE - Archives
4 Videos
- WAVE OPTICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - WAVE OPTICSEXERCISE - Assertion- Reasoning
13 Videos
- SOURCES OF MAGNETIC FIELDBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - SOURCES OF MAGNETIC FIELDEXERCISE - single correct Ansewer type
12 Videos
Similar Questions
When light from two sources (say slits S1 and S2) interfere, they form alternate dark and bright fringes. Bright fringe is formed at all point where the path difference is an odd multiple of half wavelength. At the condition of equal amplitudes, A1=A2=a, the maximum intensity will be 4a2 and the visibility improves, The resultant intensity can also be indicated with phase factor as I=2a2cos2(ϕ/2).Using this passage, answer the following questions.
At point having a path difference of λ4, the intensity
View SolutionWhen light from two sources (say slits S1 and S2) interfere, they form alternate dark and bright fringes. Bright fringe is formed at all point where the path difference is an odd multiple of half wavelength. At the condition of equal amplitudes, A1=A2=a, the maximum intensity will be 4a2 and the visibility improves, The resultant intensity can also be indicated with phase factor as I=2a2cos2(ϕ/2).Using this passage, answer the following questions.
If the path difference between the slits S1 and S2 is λ2 the central fringe will have an intensity of
View SolutionConsider interference between waves form two sources of intensities I0&4I0.Find intensities at point where the phase difference is π
View SolutionIn an interference pattern the (n+4)th blue bright fringe and nth red bright fringe are formed at the same spot. If red and blue light have the wavelength of 7800Å and 5200Å then value of n should be-
View SolutionIn an interference experiment, third bright fringe is obtained at a point on the screen with a light of 700 nm . What should be the wavelength of the light source in order to obtain 5th bright fringe at the same point
View SolutionThe distance of nth bright fringe to the nth dark fringe in Young's experiment is equal to
View SolutionIn a standard YDSE slit width is 1mm and distance of screen from the slit is 1m. If wavelength of light is 632nm and bright fringe formed at y = 1.270 mm. Find path difference for the point
View SolutionThe ratio of the intensity at the cnetre of a bright fringe to the intensity at a point one quarter of the fringe width from the centre is
View SolutionWhen two waves of intensities l1andl2 coming from coherent sources interfere at a point P, where phase difference is ϕ, then resultant intensity (lres) at point P would be
View SolutionIf S1andS2 are two point sources emitting light in phase , then what is the shape of interference fringes formed on the screen ?
View Solution
