A soap film of thickness t is surrounded by air and is illuminated at near normal incidence by monochromatic light wavelength λ in the film. With respect to the wavelength of the monochromatic light in the film, what film thickness will produce maximum constructive interference
14λ
12λ
1λ
2λ
To solve the problem of determining the film thickness t that will produce maximum constructive interference in a soap film illuminated by monochromatic light, we can follow these steps:
1. Understand the Setup:
- We have a soap film of thickness t surrounded by air.
- The film is illuminated by monochromatic light of wavelength λ in the film.
2. Identify Phase Change:
- When light reflects off a medium that is optically denser (from air to soap film), there is a phase change of π (or half a wavelength, λ/2).
- This phase change affects the condition for constructive interference.
3. Constructive Interference Condition:
- For constructive interference, the path difference must be an integer multiple of the wavelength, adjusted for any phase changes.
- The condition for constructive interference becomes:
Δx=mλ+λ2
- Here, m is an integer (0, 1, 2, ...).
4. Path Difference in the Film:
- The effective path difference for light traveling through the film and reflecting back is given by:
Δx=2t
5. Set Up the Equation:
- Equating the two expressions for path difference, we have:
2t=mλ+λ2
6. Solve for Thickness t:
- Rearranging the equation gives:
t=mλ+λ22
- This simplifies to:
t=mλ2+λ4
7. Maximize Constructive Interference:
- To find the thickness that produces maximum constructive interference, we consider the lowest order of interference, which is m=0:
t=0⋅λ2+λ4=λ4
Final Answer:
Thus, the film thickness t that will produce maximum constructive interference is:
t=λ4
- We have a soap film of thickness t surrounded by air.
- The film is illuminated by monochromatic light of wavelength λ in the film.
- When light reflects off a medium that is optically denser (from air to soap film), there is a phase change of π (or half a wavelength, λ/2).
- This phase change affects the condition for constructive interference.
- For constructive interference, the path difference must be an integer multiple of the wavelength, adjusted for any phase changes.
- The condition for constructive interference becomes:
Δx=mλ+λ2
- Here, m is an integer (0, 1, 2, ...).
- The effective path difference for light traveling through the film and reflecting back is given by:
Δx=2t
- Equating the two expressions for path difference, we have:
2t=mλ+λ2
- Rearranging the equation gives:
t=mλ+λ22
- This simplifies to:
t=mλ2+λ4
- To find the thickness that produces maximum constructive interference, we consider the lowest order of interference, which is m=0:
t=0⋅λ2+λ4=λ4
Thus, the film thickness t that will produce maximum constructive interference is:
t=λ4
Topper's Solved these Questions
- WAVE OPTICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - WAVE OPTICSEXERCISE - Integer
3 Videos
- WAVE OPTICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - WAVE OPTICSEXERCISE - Archives
4 Videos
- WAVE OPTICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - WAVE OPTICSEXERCISE - Assertion- Reasoning
13 Videos
- SOURCES OF MAGNETIC FIELDBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - SOURCES OF MAGNETIC FIELDEXERCISE - single correct Ansewer type
12 Videos
Similar Questions
A beam o monochromatic light of wavelength λ is reflected from air into water to refractive index 4/3. The wavelength of light beam inside water will be
View SolutionFor constructive interference to take place between two monochromatic light waves of wavelength λ , the path difference should be
View Solution
Knowledge Check
On introducing a thin film in the path of one of the two interfering beam, the central fringe will shift by one fringe width. If μ=1.5, the thickness of the film is (wavelength of monochromatic light is λ)
A4λB3λC2λDλ
Monochromatic light is refracted from air into the glass of refractive index μ . The ratio of the wavelength of incident and refracted waves is
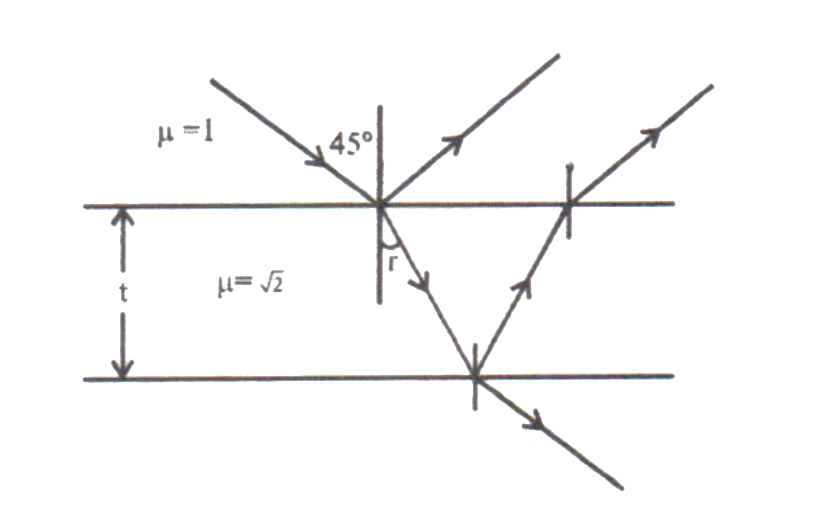
View SolutionA ray of light is incident at an angle of 45∘ (ralative to the normal) on a thin film of a liquid with an index of refraction of √2. Assuming that the medium of both sides of the film is air, find the minimum thickness of the film required for constructive interference in the reflected light for sodium light of wavelenght 600 nm.
View SolutionA thin film of thickness t and index of refractive 1.33 coats a glass with index of refraction 1.50.What is the least thickness t that will strong reflect light with wavelength 600nm incident normally?
View SolutionYoung's double slit experiment is performed with monochromatic light. A thin film is introduced in front of one of the slits
View SolutionWhat is the minimum thickness of thin film required for constructive interference in the reflected light through it ?
(Given, the refractive index of the film =1.5, wavelength of the lilght incident on the film =600 nm.
View SolutionAn oil film covers the surface of a small pond. The refractive index of the oil is greater than that of water. At one point on the film, the film has the smallest non-zero thickness for which there will be destructive interference in the reflected light when infrared radiation with wavelength 800 nm is incident normal to the film. When this film is viewed at normal incidence at this same point, for what visible wavelengths, if any, will there be constructive interference? (Visible light has wavelengths between 400nm and 700 nm )
View SolutionA light of wavelength 5890Å falls normally on a thin air film. The minimum thickness of the film such that the film appears dark in reflected light is
View Solution
