The vessel shown in the figure contains water, take ρwater=1000kg/m2,g=m/s2). For this arrangement, answer the following questions:
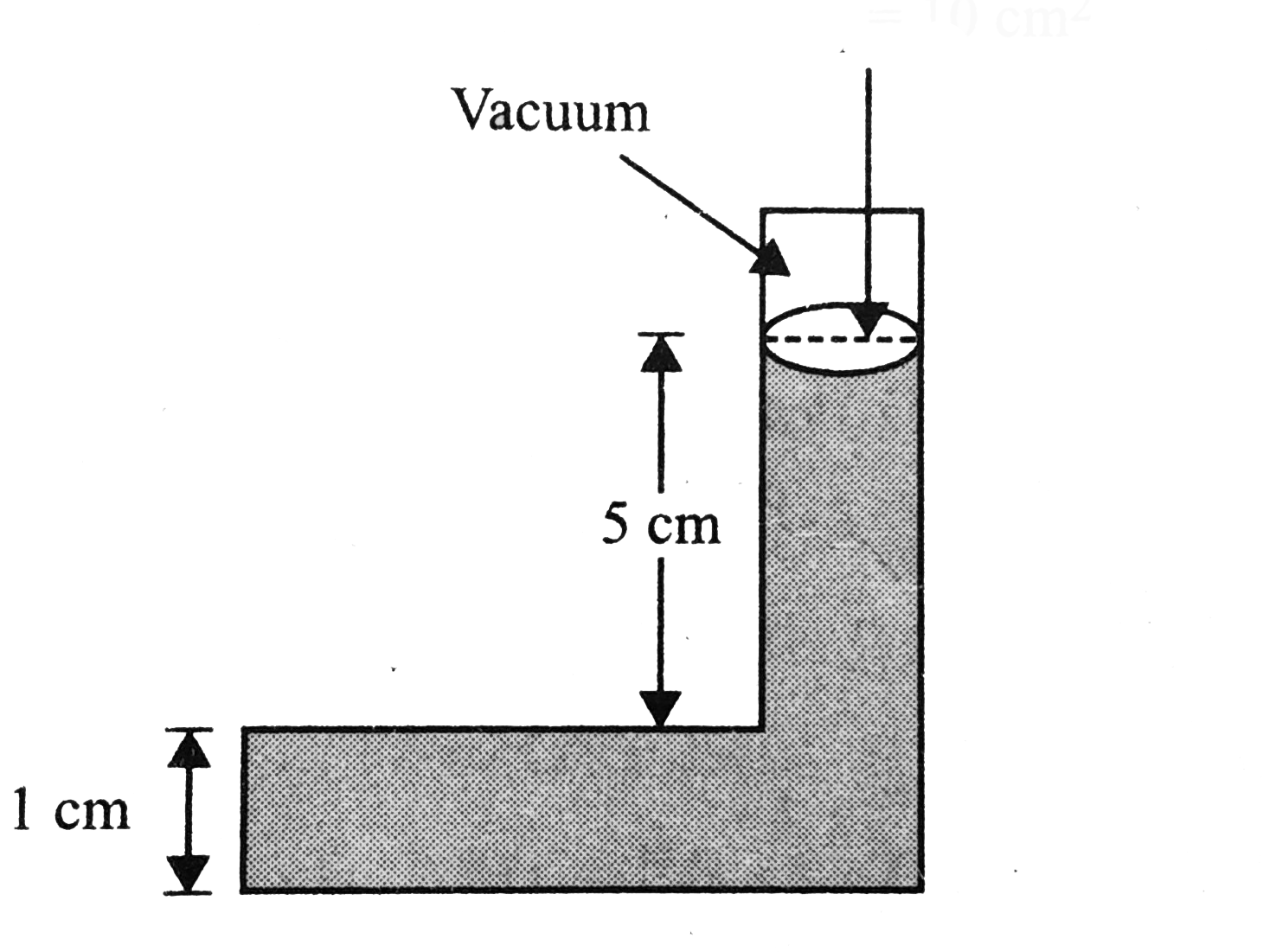
The net force acting on the base of the vessel is
Net force acting on the base of the vessel > weight of the liquid inside the vessel.
Net force acting on the base of the vessel = weight of the liquid inside the vessel.
Net pressure force acting on the liquid = weight of the vessel
Both (a) and (c) are correct.
The correct Answer is:D
Pressure at bottom of vessel
P=ρg×6cm
=1000×10×6100
=600N/m2
Force acting at the base
F=ρA2=600×50×10−4
=3N

Weight of liquid inside the vessel
W=ρ[A1×5cm+A2×1cm]g
=1000[10×5+50×1]×10−6×10=1N
So F>W
The free body diagram of the liquid is as shown. The net force on the liquid is zero.
Topper's Solved these Questions
- FLUID MECHANICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - FLUID MECHANICSEXERCISE - True/False
1 Videos
- FLUID MECHANICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - FLUID MECHANICSEXERCISE - SCQ_TYPE
13 Videos
- FLUID MECHANICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - FLUID MECHANICSEXERCISE - Assertion-Reasoning
8 Videos
- DIMENSIONS & MEASUREMENTBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - DIMENSIONS & MEASUREMENTEXERCISE - Integer
2 Videos
- GRAVITATIONBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - GRAVITATIONEXERCISE - INTEGER_TYPE
1 Videos
Similar Questions
A cylindrical object of cork of mass 15g and cross-sectional area A1=10cm2 floats in a pan of water as shown in the figure. An aluminum, cylinder of mass 25g and cross-sectional area A2=2cm2 is attached 4cm below the cork and slides through a watertight frictionless hole in the bottom of the pan. Take density of the cork, ρ=0.2g/cm3,ρaluminium=2.7g/cm3,g=10m/s2. Based on the above information, answer the following questions.

The length of the cork cylinder inside the water in equilibrium is
View SolutionA cylindrical object of cork of mass 15g and cross-sectional area A1=10cm2 floats in a pan of water as shown in the figure. An aluminum, cylinder of mass 25g and cross-sectional area A2=2cm2 is attached 4cm below the cork and slides through a watertight frictionless hole in the bottom of the pan. Take density of the cork, ρ=0.2g/cm3,ρaluminium=2.7g/cm3,g=10m/s2. Based on the above information, answer the following questions.
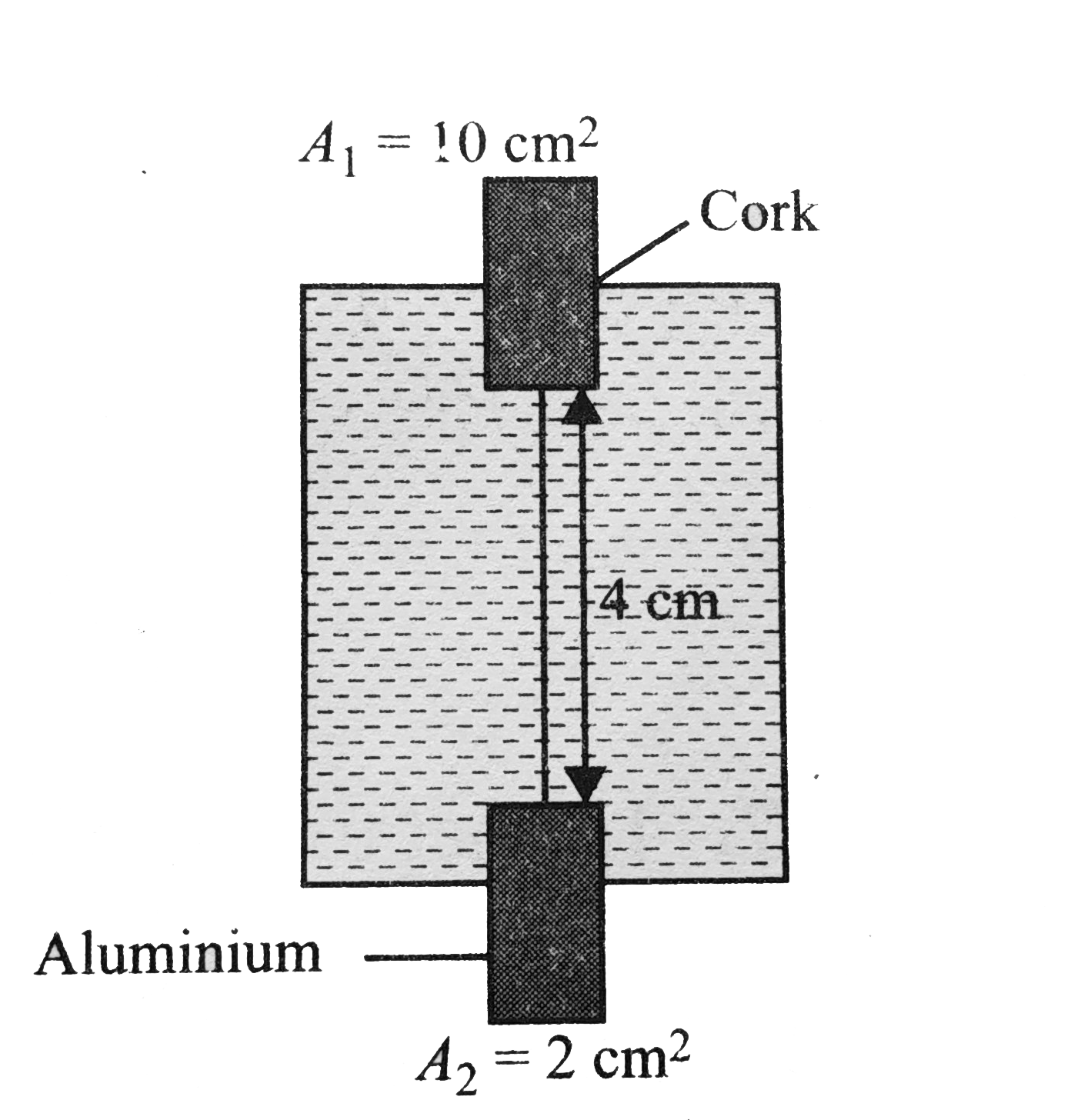
The tension in the string joining the cork and aluminium cylinder is
View Solution
Knowledge Check
Three vessels A,B,and C of different shapes contain a water upto the same height as shown in the figure .PA,PB ,and PC be the pressure exerted by the water at the bottom of the vessels A ,B and C respectively . Then
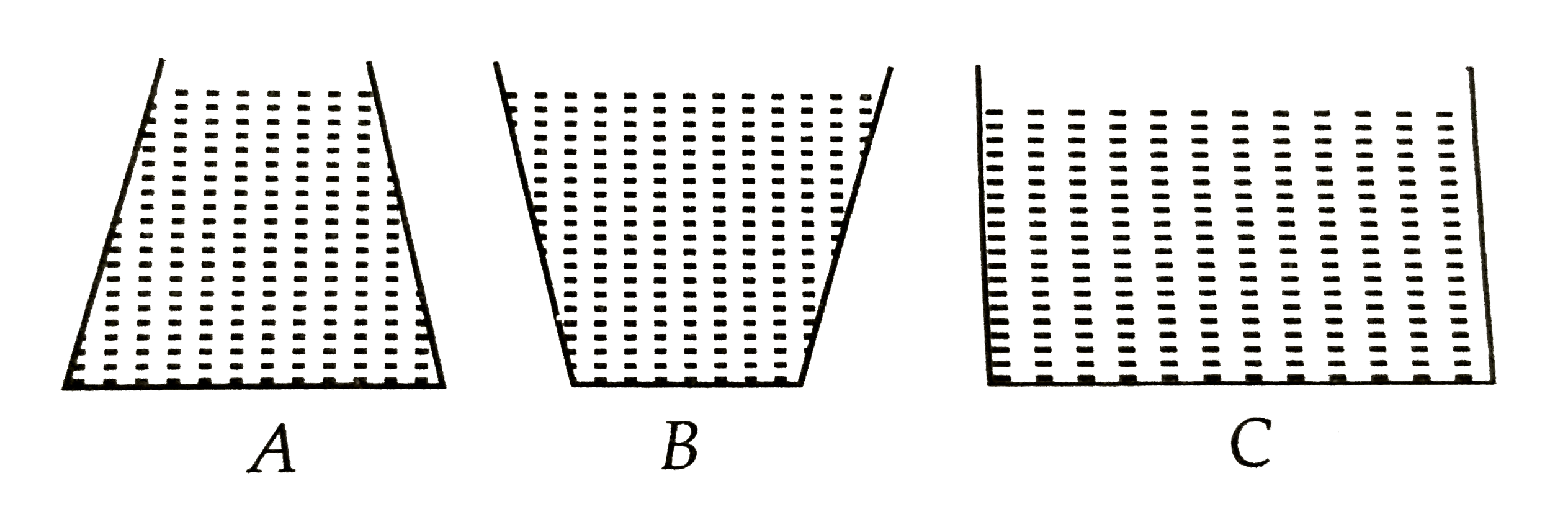 APA>PB>PCBPB>PC>PACPC>PB>PADPA=PB=PC
APA>PB>PCBPB>PC>PACPC>PB>PADPA=PB=PC
A cylindrical vessel of a very large cross sectional area is containing two immiscible liquids of density ρ1=600kg/m3 and ρ2=1200kg/m3 as shown in the figure.
A small hole having cross sectional area 5cm2 is made in right side vertical wall as shown. Take atmospheric pressure as p0=105N/m2,g=10m/s2. For this situation mark out the correct statement (s). Take cross sectional area of the cylindrical vessel as 1000cm2. Neglect the mass of the vessel.
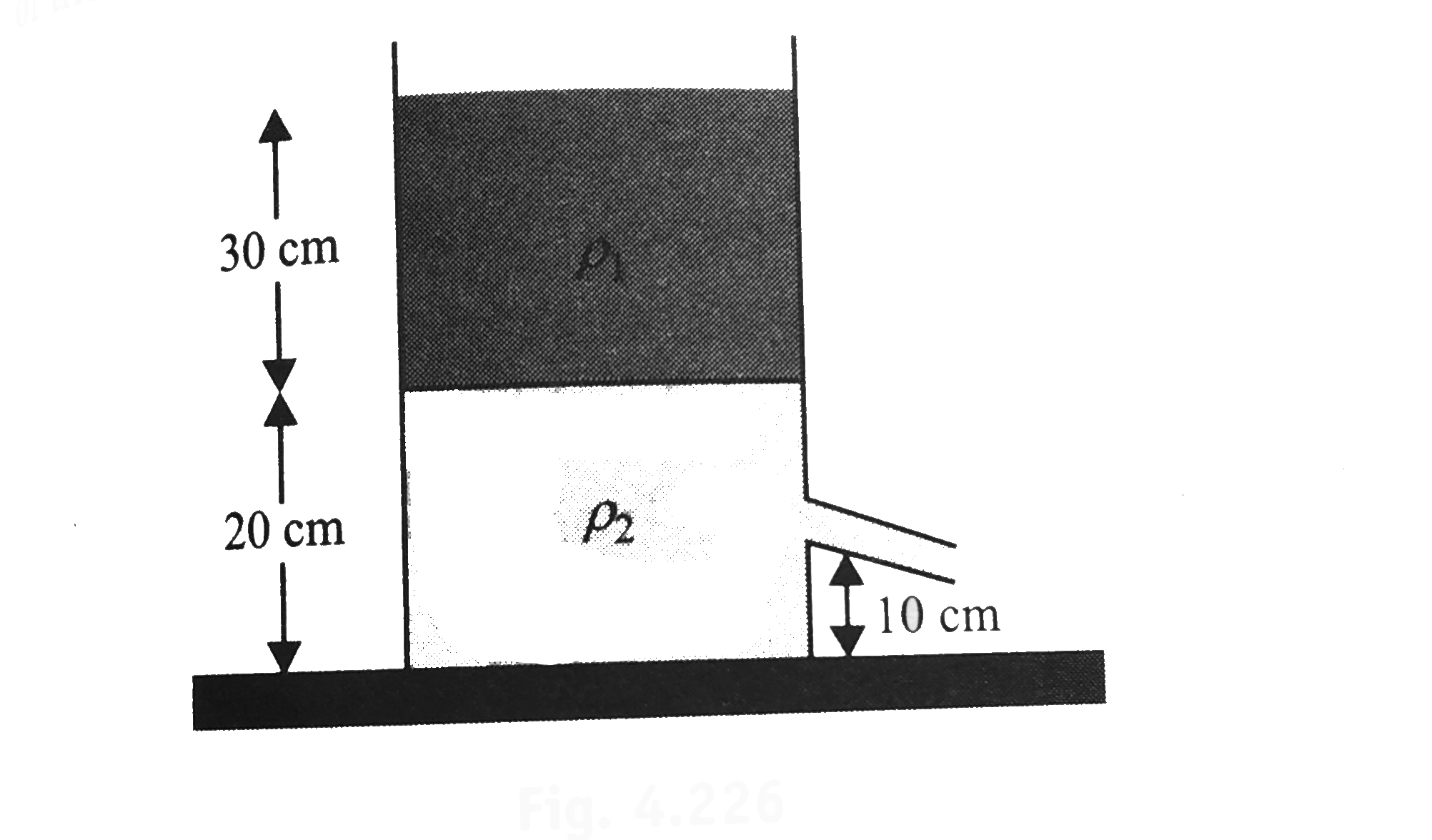
View SolutionIn the arrangement as shown, tension T2 is (g=10m/s2)
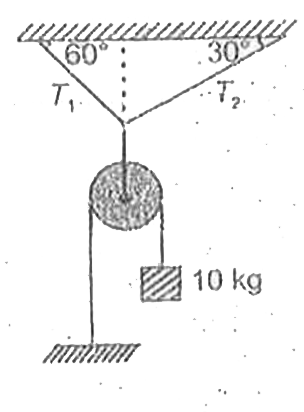
View Solution
A mass m of volume V=10cm2 is tied with a string to the base of a container filled with a liquid of density (Pl=103kg/m3) as shown in the figure. The container is then accelerated with acceleration (ax=9m/s2) and (ay=2m/s2) a shown in the figure. [g=10(ms2) acceleration due to gravity] the net buoyancy force acting on the mass is
View SolutionIn two identical communicating vessel we poured water (see picture). In one of them we put an ice ball of volume V=100cm3 which gets exactly half immersed in the water. The density of water ρw=1000kg/m3 the density of ice ρi=900kg/m3

Select the correct statement (s). Soon after placing the ice ball in left vessel.
View SolutionA solid cylinder of height h and mass m is floating in a liquid of density ρ as shown in the figure. Find the acceleration of the vessel (in m/s2) containing liquid for which the relative downward acceleration of the completely immersed cylinder w.r.t. vessel becomes equal to one-third of that of the vessel. (Take g = 10 m//s^(2))
View SolutionA solid cylinder of height h and mass m is floating in a liquid of density ρ as shown in the figure. Find the acceleration of the vessel (in m/s2) containing liquid for which the relative downward acceleration of the completely immersed cylinder w.r.t. vessel becomes equal to one-third of that of the vessel. (Take g=10m/s2)

View SolutionA wooden rod weighing 25N is mounted on a hinge below the free surface of water as shown. The rod is 3m long and uniform in cross section and the support is 1.6m below the free surface. At what angle α rod is in equilibrium? The cross-section of the rod is 9.5×10−4m2 in area. Density of water is 1000kg/m3. Assume buoyancy to act at centre of immersion. g=9.8m/s2. Also find reaction on the hinge in this position.
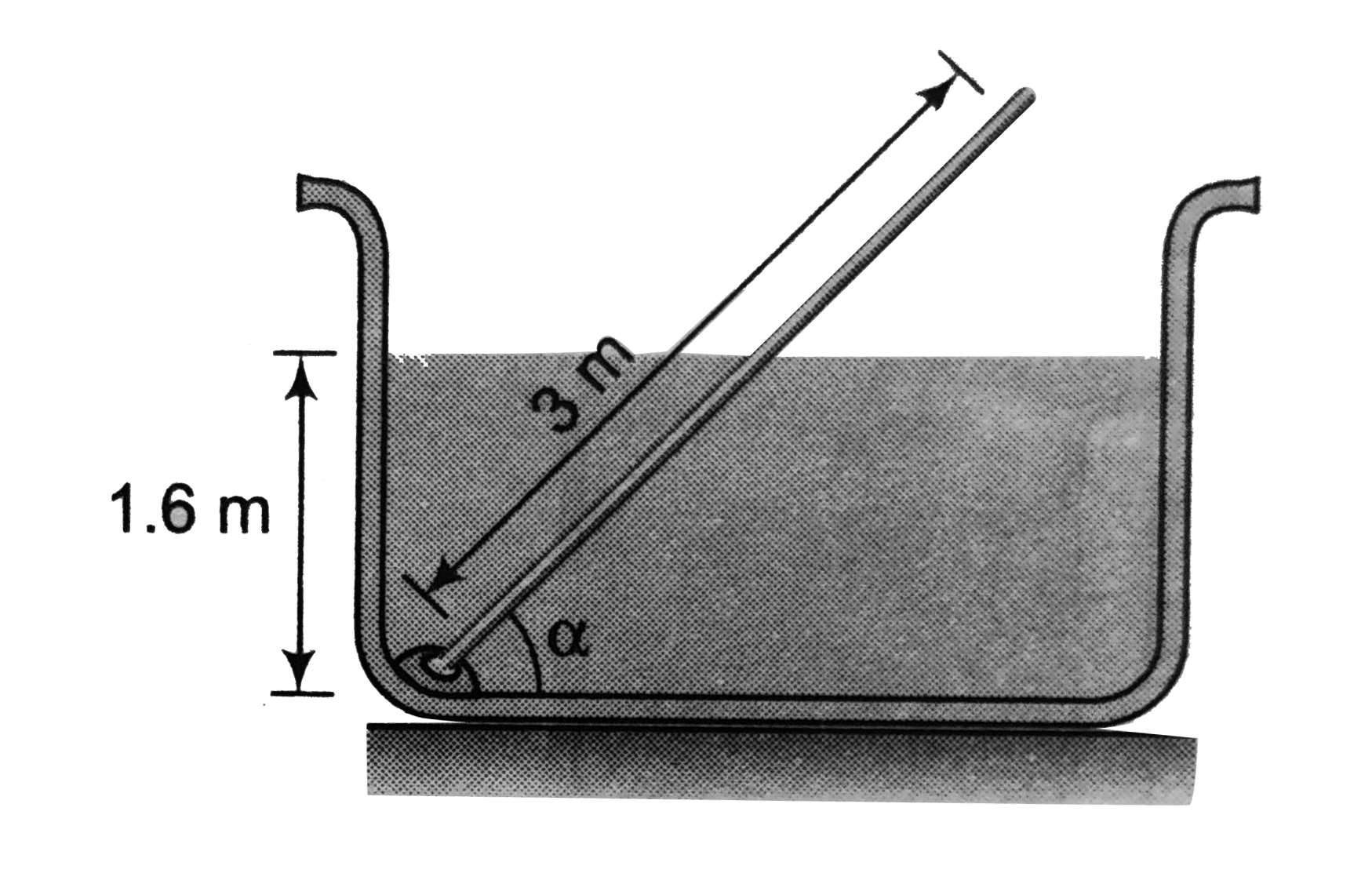 .
.
View Solution
