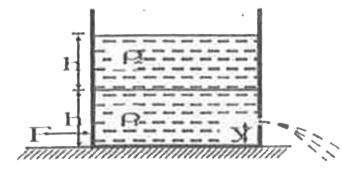
A cylindrical vessel of a very large cross sectional area is containing two immiscible liquids of density ρ1=600kg/m3 and ρ2=1200kg/m3 as shown in the figure.
A small hole having cross sectional area 5cm2 is made in right side vertical wall as shown. Take atmospheric pressure as p0=105N/m2,g=10m/s2. For this situation mark out the correct statement (s). Take cross sectional area of the cylindrical vessel as 1000cm2. Neglect the mass of the vessel.
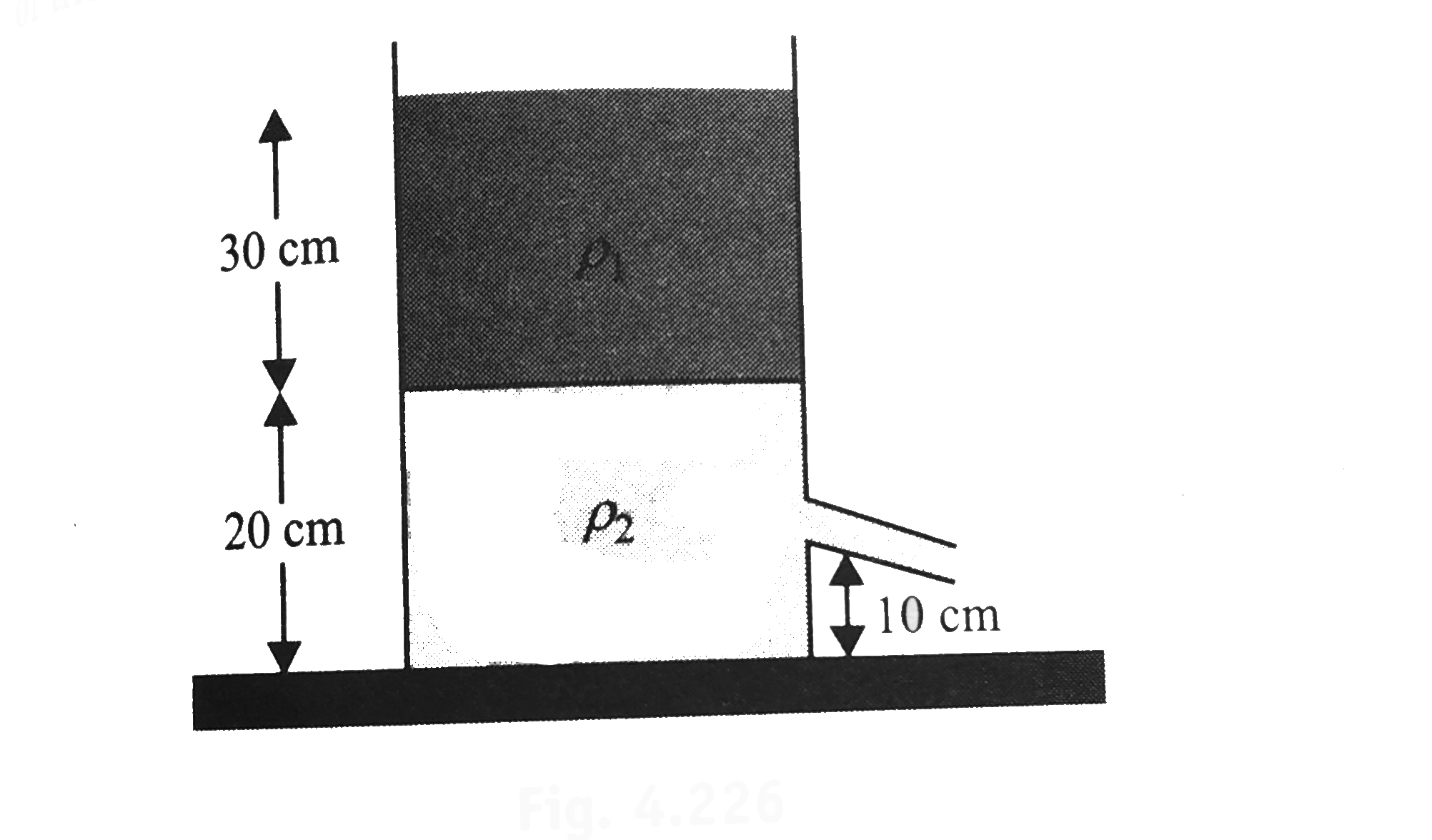
If the surface on which the vessel is placed is smooth, then a rightward force of magnitude 3N is to be applied on the vessel to maintain its static equilibrium.
If the surface on which the vessel is placed is smooth, then no force is needed to maintain its static equilibrium.
If the surface on which the vessel is placed is rough (μ=0.04), then the minimum force (horizontal) needed to be applied on the vessel to maintain its static equilibrium is zero.
If the surface on which the vessel is placed is rough (=0.04) then the maximum force (horizontal) needed to be applied on the vessel to maintain its static equilibrium is 19.8N.
The correct Answer is:A, C, D
The velocity with which the liquid comes out is given by the expression
P0+ρ1g×30cm=ρ2g×10cm=p0+ρ2v22
v=2.24m/s
Due to transfer of liquid, change in moment takes place and hence a force has been exerted on the liquid in backward direction, this force is given by F=ρ2av2, where a is the cross sectional area of hole =1200×5×10−4×5=3N
Normal contact force betwen the vessel and the suface is
N=mg
N=(ρ1A×0.3)g+(ρ2×A×0.2)G=420
Where A is the cross sectional area of te vessel. Limiting friction force,
fL=μN=0.04×420=16.8
As fL>F, therefore the minimum force necessary to maintain the static equilibrium is 0. For the maximum value of the applied force
Fmax=fL+F=16.8+3=19.8n
Topper's Solved these Questions
- FLUID MECHANICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - FLUID MECHANICSEXERCISE - Multipe Correct
15 Videos
- FLUID MECHANICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - FLUID MECHANICSEXERCISE - Assertion-Reasoning
8 Videos
- FLUID MECHANICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - FLUID MECHANICSEXERCISE - Subjective
25 Videos
- DIMENSIONS & MEASUREMENTBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - DIMENSIONS & MEASUREMENTEXERCISE - Integer
2 Videos
- GRAVITATIONBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - GRAVITATIONEXERCISE - INTEGER_TYPE
1 Videos
Similar Questions
A cylindrical tank having cross-sectional area A=0.5m2 is filled with two liquids of density ρ1=900kgm−3 and ρ2=600kgm−3, to a height h=60cm each as shown in the figure. A small hole having area a=5cm2 is made in right vertical wall at a height y=20cm from the bottom. A horizontal force F is applied on the tank to keep it in static equilibrium. The tank is lying on a horizontal surface. Neglect mass of the cylindrical tank in comparison to mass of the liquids (Take g = 10 ms^(-2)).
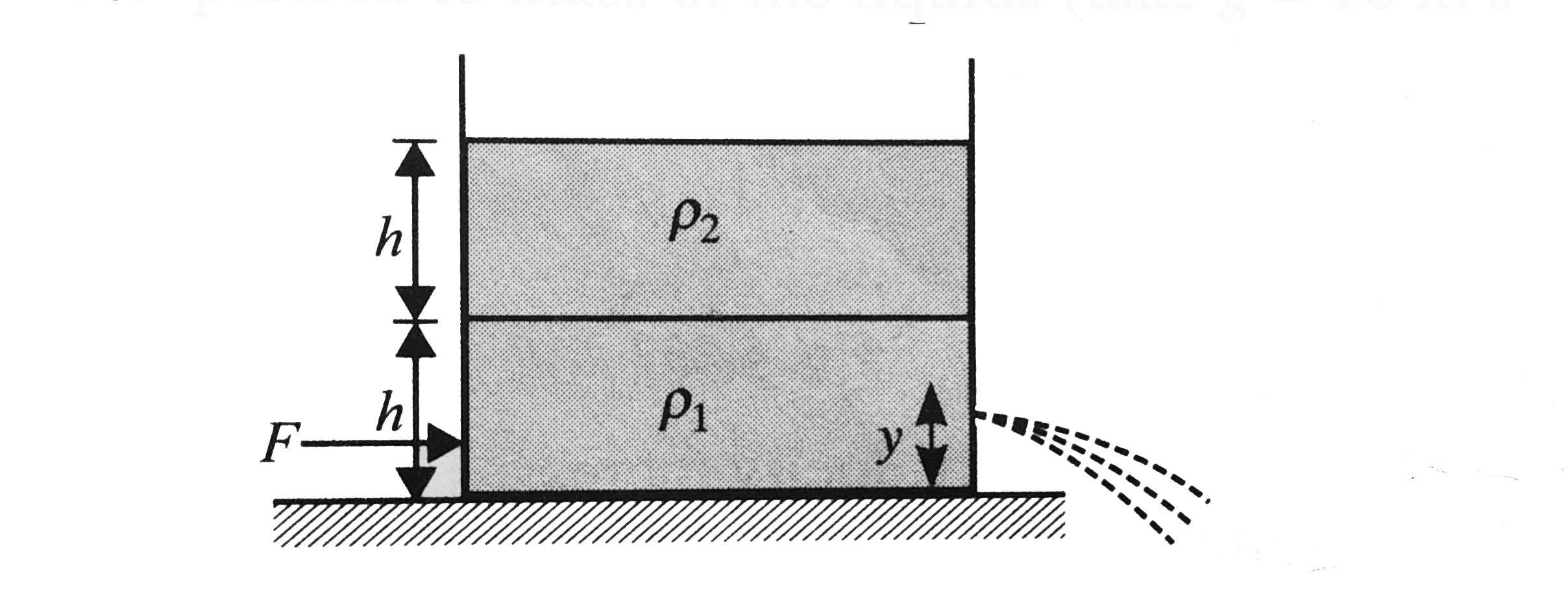
The velocity of efflux is
View SolutionA cylindrical tank having cross-sectional area A=0.5m2 is filled with two liquids of density ρ1=900kgm−3 and ρ2=600kgm−3, to a height h=60cm each as shown in the figure. A small hole having area a=5cm2 is made in right vertical wall at a height y=20cm from the bottom. A horizontal force F is applied on the tank to keep it in static equilibrium. The tank is lying on a horizontal surface. Neglect mass of the cylindrical tank in comparison to mass of the liquids (akeg = 10 ms^(-2)).
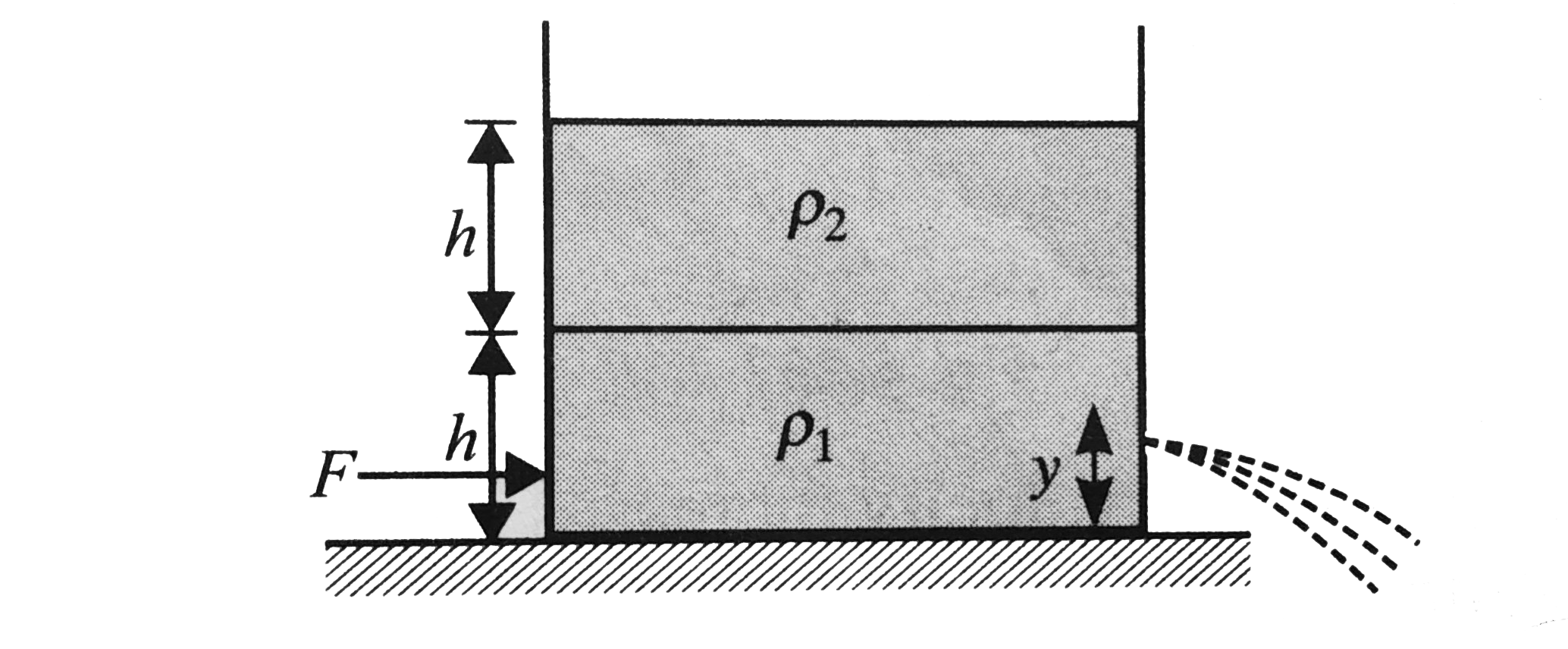
The horizontal force required to keep the cylinder in static equilibrium, on a smooth horizontal plane is
View SolutionA cylindrical tank having cross-sectional area A=0.5m2 is filled with two liquids of density ρ1=900kgm−3 and ρ2=600kgm−3, to a height h=60cm each as shown in the figure. A small hole having area a=5cm2 is made in right vertical wall at a height y=20cm from the bottom. A horizontal force F is applied on the tank to keep it in static equilibrium. The tank is lying on a horizontal surface. Neglect mass of the cylindrical tank in comparison to mass of the liquids (akeg=10ms−2).
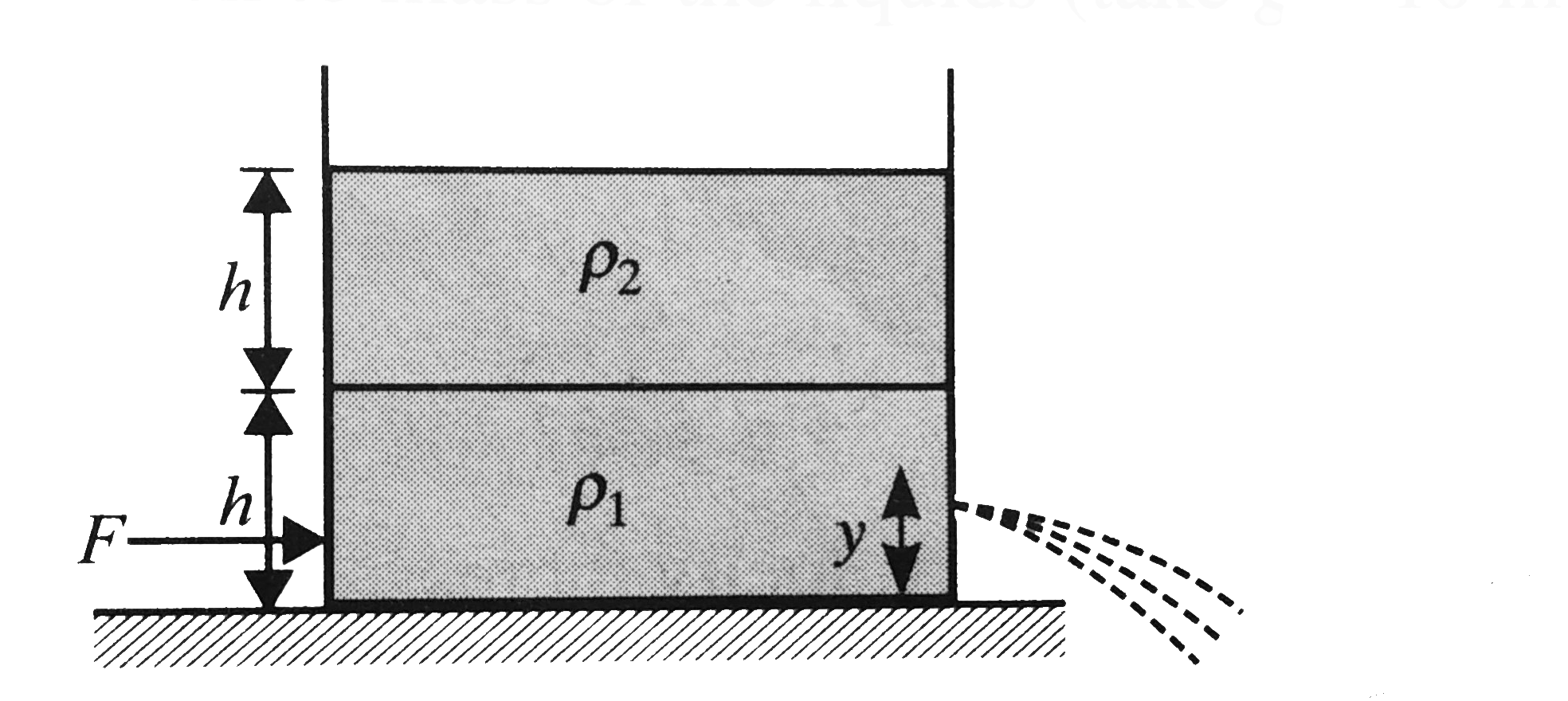
(i) horizontal force F to keep the cylinder in static equilibrium, if it is placed on a smooth horizontal plane and (ii) minimum and maximum values of F to keep the cylinder in static equilibrium, if coefficient of friction between the cylinder and the plane is µ = 0.01. (g = 10 ms –2 )
View SolutionThe velocity of the liquid coming out of a small hole of a vessel containing two different liquids of densities 2ρ and ρ as shown in the figure is

View SolutionThe velocity of the liquid coming out of a small hole of a vessel containing two different liquids of densities 2ρ and ρ as shown in the figure is

View SolutionA cylindrical tank having cross - sectional area A=0.5m2 is filled with two liquids of density ρ1=900 kg m−3andρ2=600 kg m−3 , to a height h =60cm2each.A small hole having area a=5 cm^2 is made in right vertical wall at a height y = 20 cm from the bottom . A horizontal force F is applied on the tank to keep it in static equilibrium . The tank is lying on a horizontal surfaces . Neglect mass of cylindrical tank camparison to mass of liquids ( take g=10ms−2)
Horizontal force F to keep the cylinder in static equilibrium , if it is placed on a smooth horizontal thrust exerted by fluid jet . But that is equal to mass flowing per second × change in velocity of this mass
∴ F=(avρ)(v−0)=aρv2
or F=7.2N
View SolutionThe vessel shown in the figure contains water, take ρwater=1000kg/m2,g=m/s2). For this arrangement, answer the following questions:
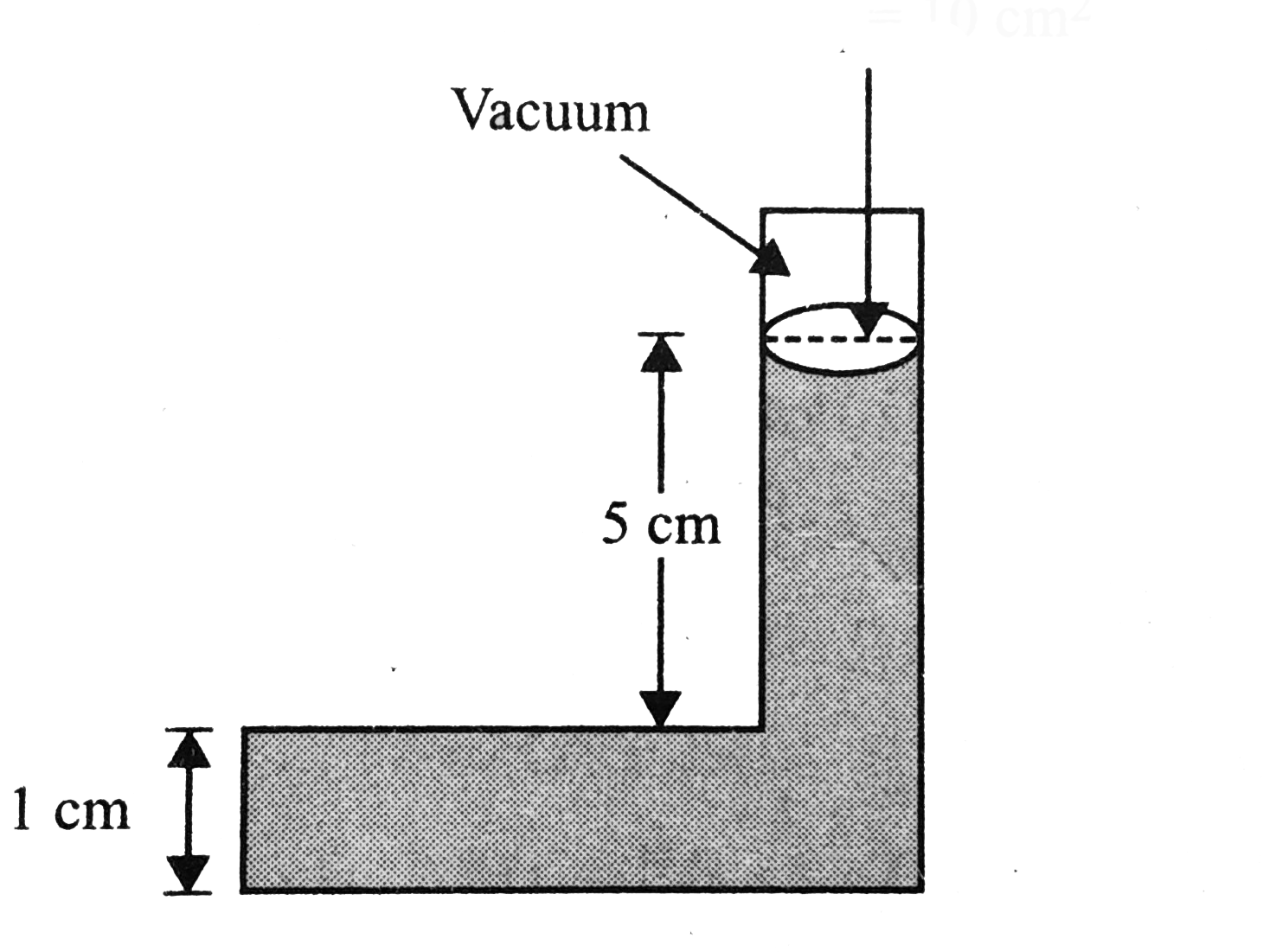
The net force acting on the base of the vessel is
View SolutionA cylindrical tank having cross - sectional area A=0.5m2 is filled with two liquids of density ρ1=900 kg m−3andρ2=600 kg m−3 , to a height a =6cm2 is made in right vertical wall at a height y = 20 cm from the bottom . A horizontal force F is applied on the tank to keep it in static equilibrium . The tank is lying on a horizontal surfaces . Neglect mass of cylindrical tank camparison to mass of liquids ( take g=10ms−2)
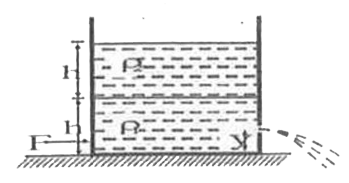
Minimum and maximum values of F to keep the cylinder in static just after the water starts to spill through the hole . If the co - efficient of static friction between contact surfaces is 0.01
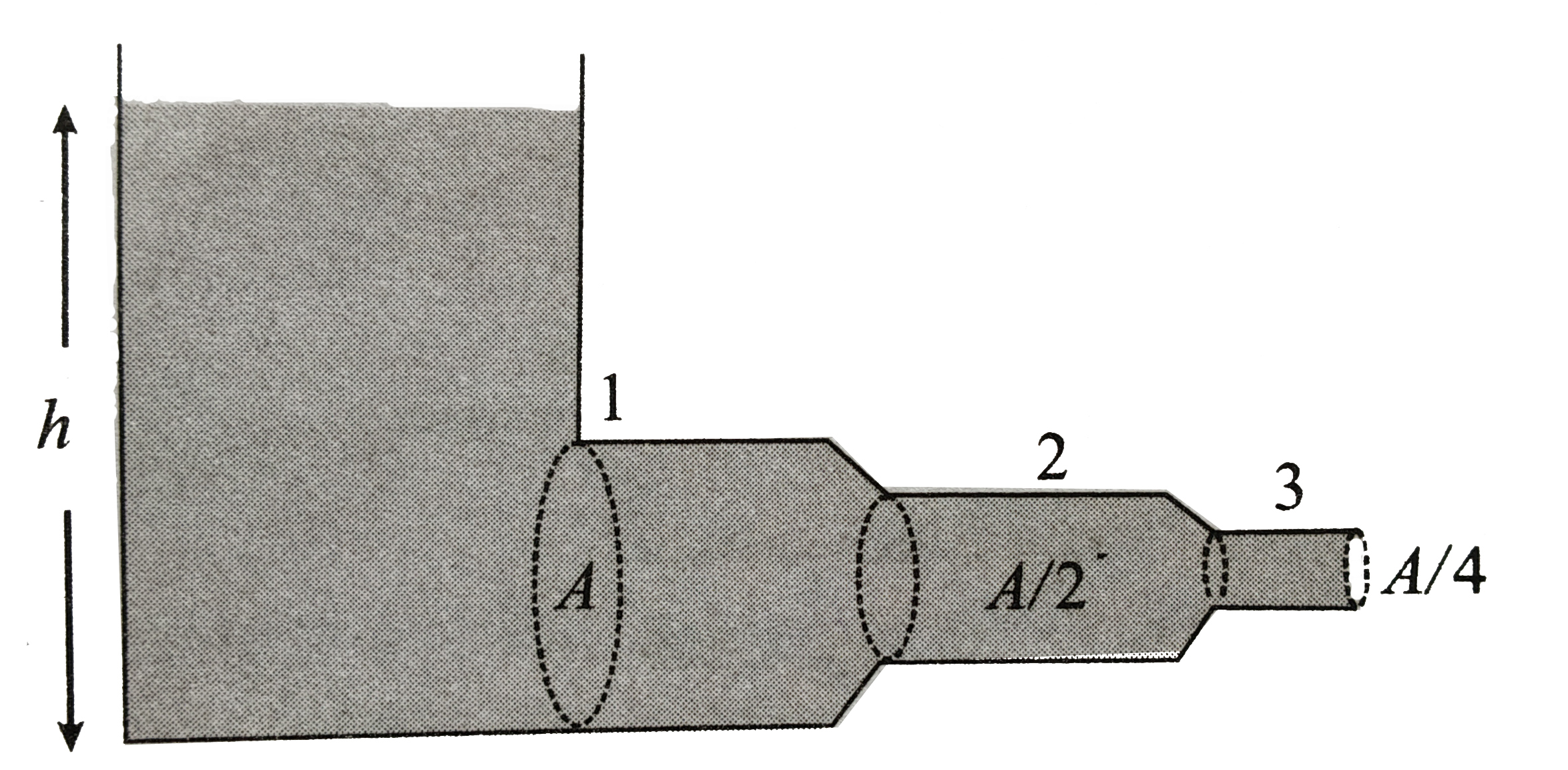
View SolutionIn the figure shown the velocity and pressure of the liquid at the cross section (2) are given by (If P0 is the atmospheric pressure).
View SolutionThe level of water in a tank is 5 m high. A hole of area of cross section 1 cm2 is made at the bottom of the tank. The rate of leakage of water for the hole in m3s−1 is (g=10ms−2)
View Solution
