Length of a horizontal arm of ends of both the vertical arms pressure P0=105N/m2. A liquid of density ρ=103kg/m3 is poured in the tube such that liquid just fills the horizontal part of the tube as a shown in Fig. Now one end of the open ends is sealed and the tube is then rotated about a vertical axis passing through the other vertical arm with angular speed ω0=√40/3rad/sec. If length of each vertical arm is a=1m and in the sealed end liquid rises to a height y=1/2m, find pressure in the sealed tube during rotation. (in ×105N/m2)

The correct Answer is:1
When the tube is rotated, the liquid starts to flow radially outwards and air in sealed arm is compressed. Let the shift of the liquid be y shown in figure.

Let the cross sectional area of the tube be S. Here element of length dx is rotating with the tube. From the free body diagram of the element we can write
(P+dP)S−PS=dmω2x=(ρSdx)ω2x
dPS=ρω2Sxdx
Here the pressure diference beween points A and B can be given by integrating the pressure difference across an element of width dx, which is given as
dP=ρω2xdx
Now integrating from A to B we get
PB−PA=∫Lvρω2xdx=ρω22(L2−y2)
⇒PB=p0+ρω22(L2≡y2)
The pressure at point C can be given as
PC=Pa−yρg
At point A, pressure is atmosphere. Thus, we have
PC=ρω22(L2−y2)+P0−yrhog=105N/m
Topper's Solved these Questions
- FLUID MECHANICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - FLUID MECHANICSEXERCISE - True/False
1 Videos
- FLUID MECHANICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - FLUID MECHANICSEXERCISE - SCQ_TYPE
13 Videos
- FLUID MECHANICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - FLUID MECHANICSEXERCISE - Assertion-Reasoning
8 Videos
- DIMENSIONS & MEASUREMENTBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - DIMENSIONS & MEASUREMENTEXERCISE - Integer
2 Videos
- GRAVITATIONBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - GRAVITATIONEXERCISE - INTEGER_TYPE
1 Videos
Similar Questions
Length of horizontal arm of a uniform cross section U-tube is l=21cm and ends of both of the vertical arms are open to surrounding of pressure 10500N/m2. A liquid of density ρ=103kg/m3 is poured into the tube such that liquid just fills the horizontal part of the tube. Now one of the open ends is sealed and the tube is then rotated about a vertical axis passing through the other vertical arm With angular velocity ω0=10rad/s. If length of each vertical arm is a=6cm, calculate the length of air column in the sealed arm. (in cm)

View SolutionLength of the horizontal arm of a uniform cross - section U - tube is l = 5 cm and both ends of the vertical arms are open to the surrounding pressure of 7700 N m−2. A liquid of density ρ=103 kg m−3 is poured into the tube such that the liquid just fills the horizontal part of the tube. Now, one of the open ends is sealed and the tube. Now, one of the open ends is sealed and the tube is then rotaed about a vertical axis passing through the other veritcal arm with angular velocity ω due to which the liquid rises up to half the length of the vertical arm. If length of each vertical arm is a = 6 cm. What is the value of ω(in rad s−1)?
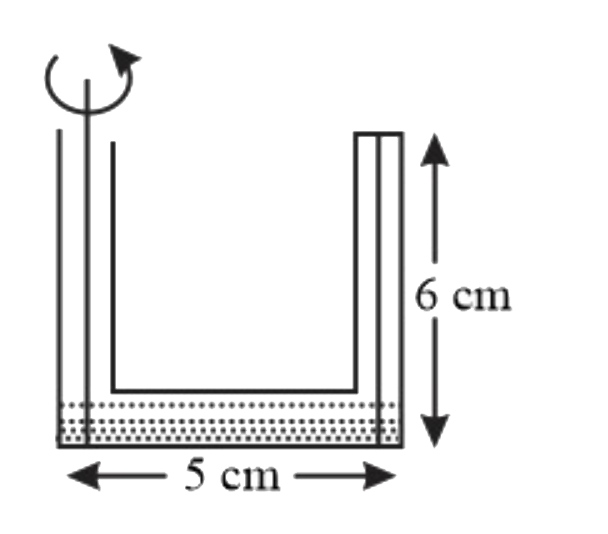
View SolutionA vertical U-tube is spinned about the vertical axis passing through the left hand limb, with an angular speed ω such that the liquid columns in the limbs have heights h and 3h, as shown in the figure. Find the value of to ω.
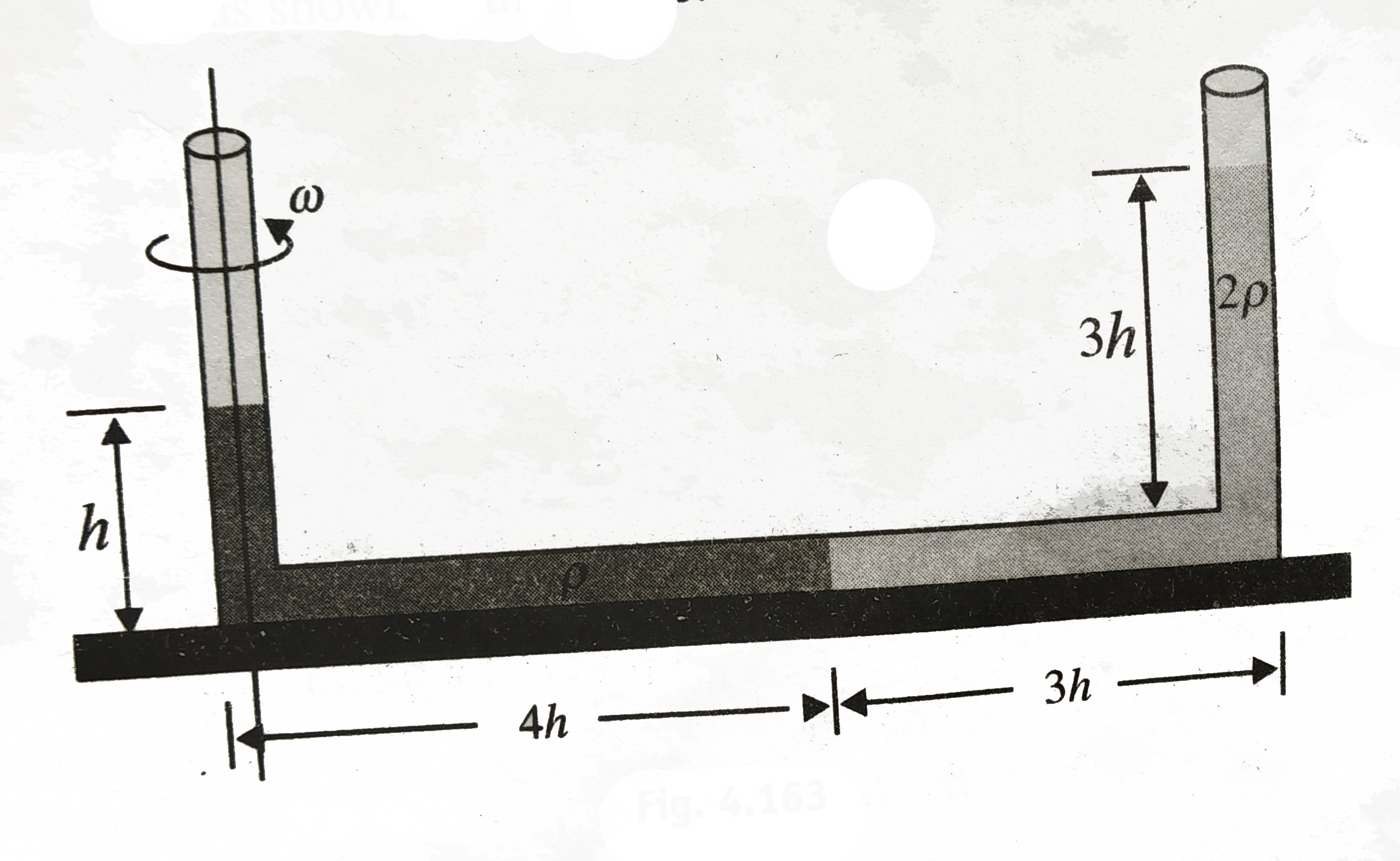
View SolutionA liquid of density ρ is filled in a U-tube is accelerated with an acceleration a so that the height of liquid in its two vertical arms are h1andh2 as shown in the figure. If l is the length of horizontal arm of the tube, the acceleration a is
View SolutionA uniform rod of mass m and length l rotates in a horizontal plane with an angular velocity ω about a vertical axis passing through one end. The tension in the rod at a distance x from the axis is
View SolutionA uniform rod of mass m and length L is free to rotate in the vertical plane about a horizontal axis passing through its end. The rod initially in horizontal position is released. The initial angular acceleration of the rod is:

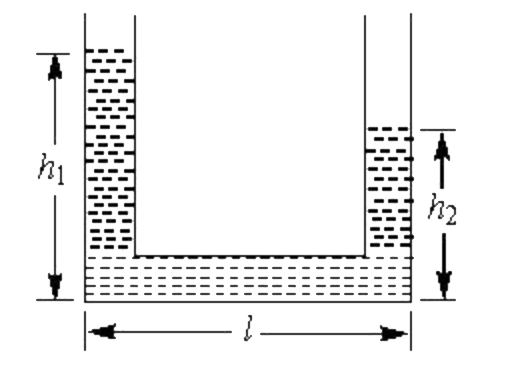
View SolutionIn the given tube liquid density ρ is filled. Find the acceleration of the tuve towards right direction such that no liquid will fall out of the tube.
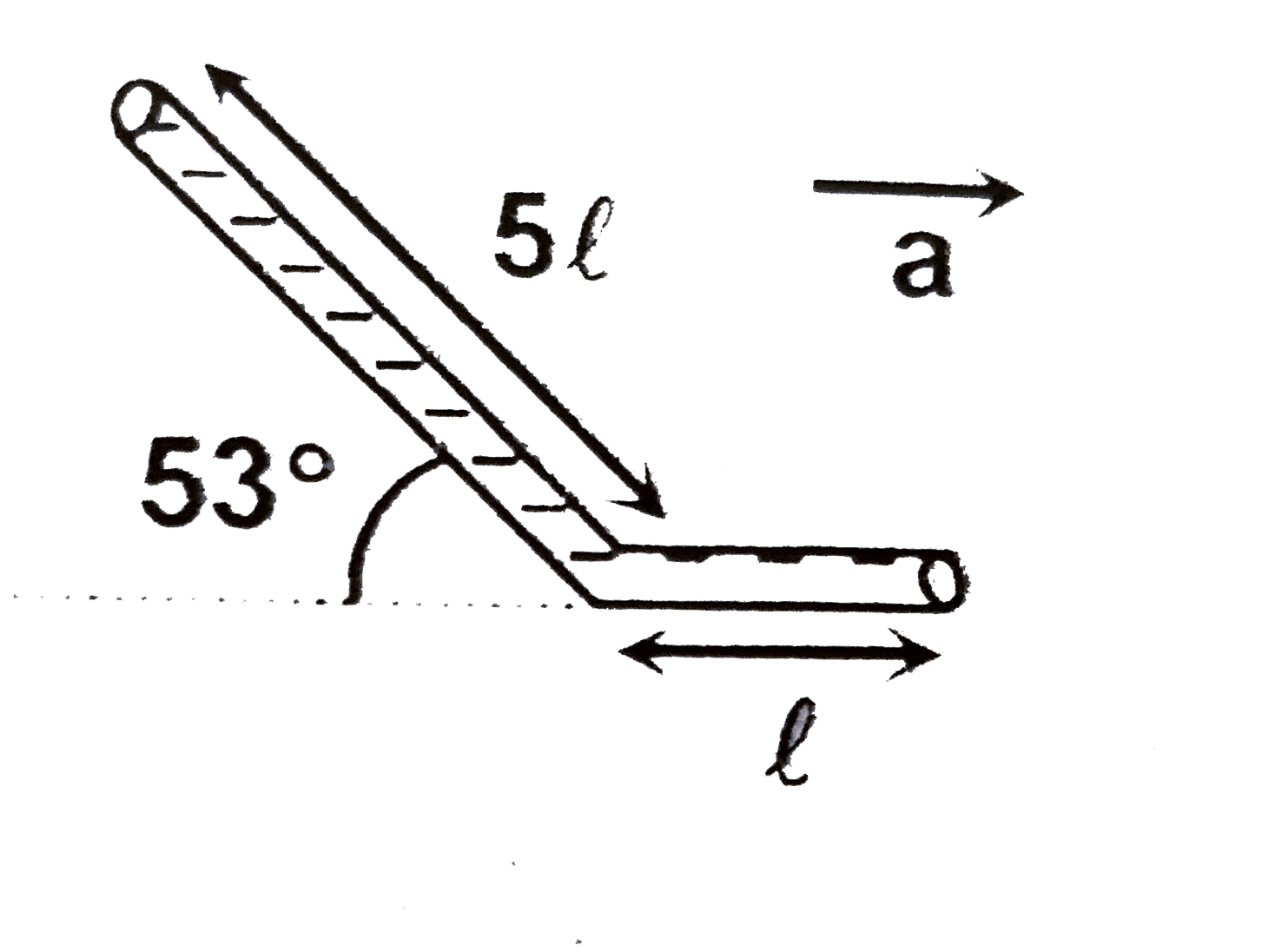
View Solution_S01_079_Q01.png)
A horizontal oriented tube AB of length 5m rotates with a constant angular velocity 0.5 rad/s about a stationary vertical axis OO' passing through the end A. the tube is filled with ideal fluid. The end of the tube is open, the closed end B has a very small orifice. The velocity with which the liquid comes out from the hole (in m/s) is
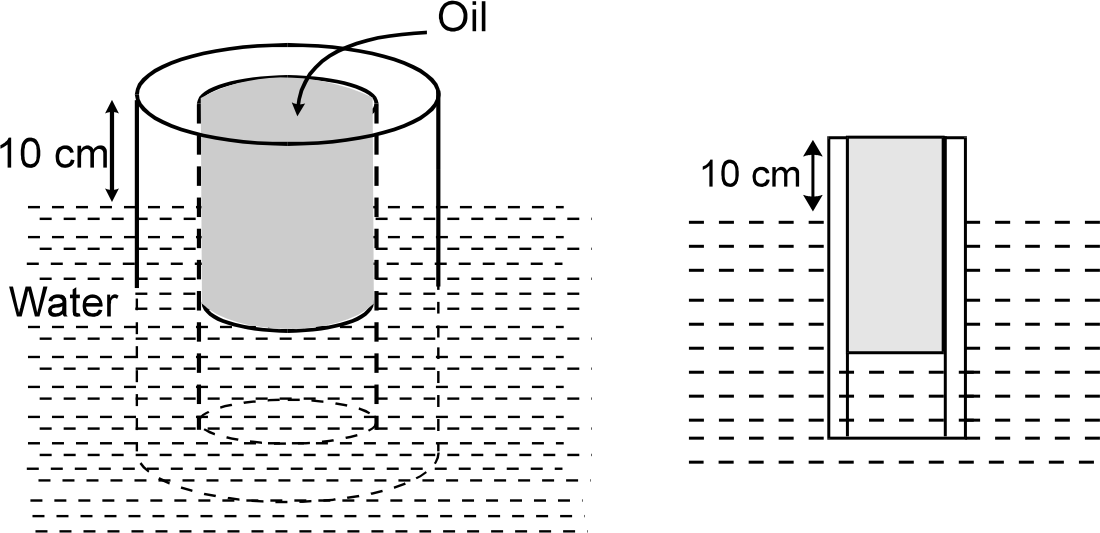
View SolutionA tube with both ends open floats vertically in water. Oil with a density 800 kg/m3 is poured into the tube. The tube is filled with oil upto the top end while in equilibrium. The portion out of the water is of length 10 cm. The length of oil in the tube is 10αcm. Find α (assume effect of surface tension is neglible):
View SolutionA non viscous liquid of density ρ is filled in a tube with A as the area of cross section, as shown in the figure. If the liquid is slightly depressed in one of the arms, the liquid column oscillates with a frequency

View Solution
