A solid cylinder of height h and mass m is floating in a liquid of density ρ as shown in the figure. Find the acceleration of the vessel (in m/s2) containing liquid for which the relative downward acceleration of the completely immersed cylinder w.r.t. vessel becomes equal to one-third of that of the vessel. (Take g=10m/s2)

The correct Answer is:5
Let the volume of the cylinder be V. When the cylinder is floating, upthrust=weight. Hence
ρ=(34V)g=mg⇒V=4m3ρ
Let the acceleration of the particle vessel be A (upwards). In the reference frame of the vessel, the acceleration of the cylinder is A.3.
∴mg+mA−upthrust=m(A3)
mg+mA−ρVg'=m(A3)
Where g'=g+A=effective value of g for upthrust
∴mg+mA−ρV(g+A)=m(A3)
⇒mg−43mg(g+A)=−m23A
A=(−g2)upwards
The acceleration of the vessel should be g=102=5ms−2 (downwards)
Topper's Solved these Questions
- FLUID MECHANICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - FLUID MECHANICSEXERCISE - True/False
1 Video
- FLUID MECHANICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - FLUID MECHANICSEXERCISE - SCQ_TYPE
13 Videos
- FLUID MECHANICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - FLUID MECHANICSEXERCISE - Assertion-Reasoning
8 Videos
- DIMENSIONS & MEASUREMENTBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - DIMENSIONS & MEASUREMENTEXERCISE - Integer
2 Videos
- GRAVITATIONBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - GRAVITATIONEXERCISE - INTEGER_TYPE
1 Video
Similar Questions
A solid cylinder of mass M and radius R pure rolls on a rough surface as shown in the figure. Choose the correct alternative (s).

View SolutionA block of volume V and density ρ is floating in a liquid of density 2ρ filled in a vessel. Now the vesset starts falling freely with acceleration g. Then the volume of block inside the liquid in the falling condition is
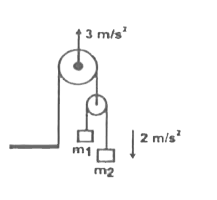
View SolutionIn the figure shown, the acceleration of block of mass m2 is 2m/s2. The acceleration of m1 :
View SolutionA wooden block is floating in a liquid. About 50% of its volume is inside the liquid when the vessel is stationary, Percentage volume immersed when the vessel moves upwards with acceleration a=g2 is
View SolutionA wooden block is floating in a liquid. About 50% of its volume is inside the liquid when the vessel is stationary, Percentage volume immersed when the vessel moves upwards with acceleration a=g.2 is
View SolutionConsider a solid cylinder of the density ρs cross section area A and h ploating in a liquid of density ρl as shown in figure (ρl>ρs) . It is depressed sligtly and allowed to oscillation.

View SolutionFind the acceleration of the two blocks shown in figure-2.101.Take g=10m/s2
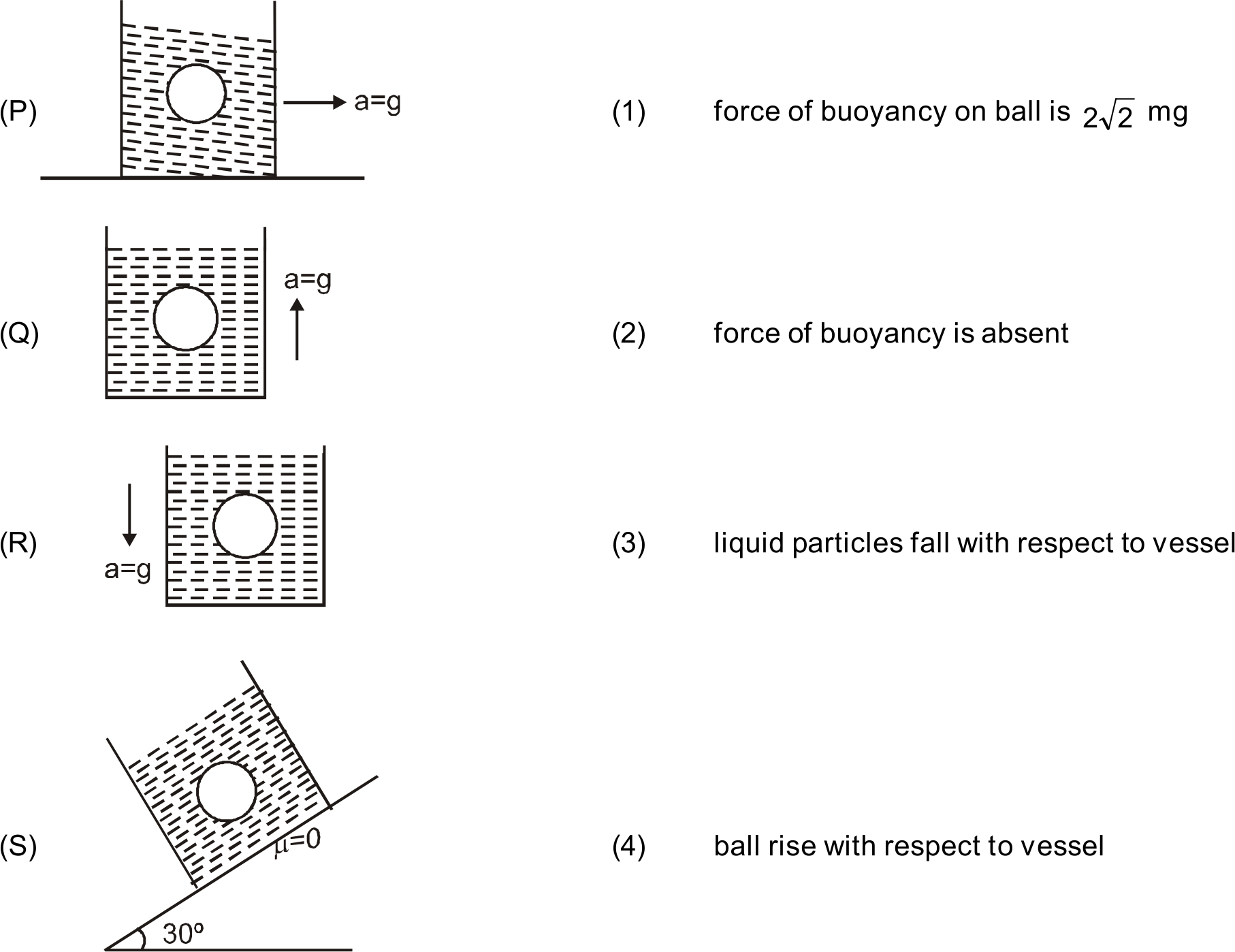
View SolutionA ball of mass m and density ρ2 is completely immersed in a liquid of density ρ, contained in an accelerating vessel as shown.Select the correct answer using the codes given below the columns.
View SolutionA plank of mass M, is placed on a smooth surface over which a cylinder of mass m(=M) annd radius R=1m is placed as shown in figure. Now the plane is pulled towards the right wilth an external force F(=2Mg). If the cyinder does not slip over the surfcace of the plank, find the linear acceleration of he plank and the cylinder and the angular acceleration of the cylinder. (Take g=10ms2)

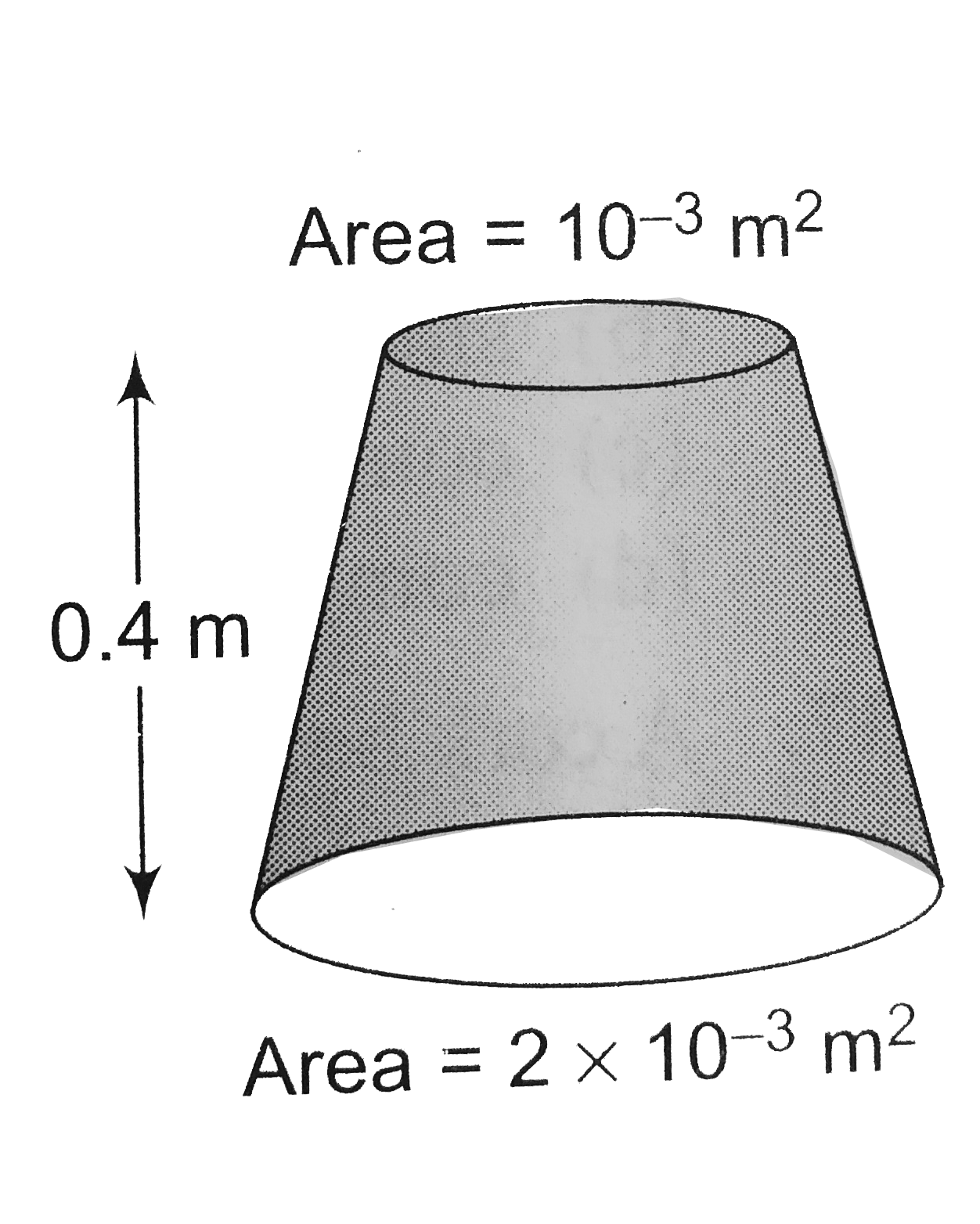
View SolutionA uniformly tapering vessel is filled with a liquid of density 900km/m3. The force that acts on the base of the vessel due to the liquid is (g=10ms−2)
View Solution
