A vertical U-tube is spinned about the vertical axis passing through the left hand limb, with an angular speed ω such that the liquid columns in the limbs have heights h and 3h, as shown in the figure. Find the value of to ω.
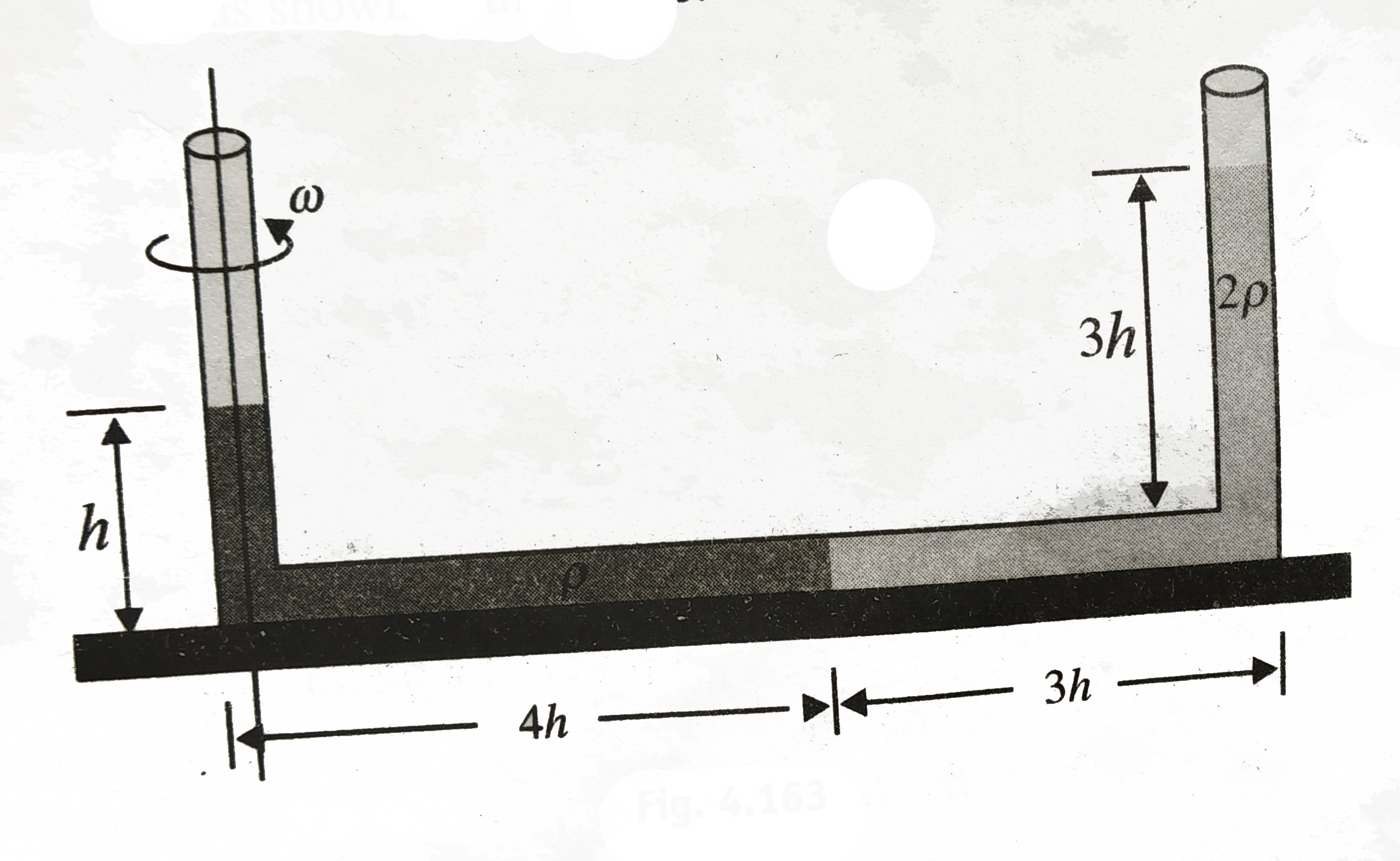
The correct Answer is:√5g41h
Let pressure at P be p1 Now at a distance x

p−p1=ρω22[x2]4h0
p−p1=ρω22×16h2…..i
p2−p=2ρω22[x2]7h4h
p2−p=ρω2×(33h2)………ii
Adding eqn i and ii p2−p1=41ρω2h2
5ρgh=41ρh2ω2⇒√5g41h=ω
Topper's Solved these Questions
- FLUID MECHANICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - FLUID MECHANICSEXERCISE - Single Correct
95 Videos
- FLUID MECHANICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - FLUID MECHANICSEXERCISE - Multipe Correct
15 Videos
- FLUID MECHANICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - FLUID MECHANICSEXERCISE - Exercise 4.4
10 Videos
- DIMENSIONS & MEASUREMENTBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - DIMENSIONS & MEASUREMENTEXERCISE - Integer
2 Videos
- GRAVITATIONBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - GRAVITATIONEXERCISE - INTEGER_TYPE
1 Video
Similar Questions
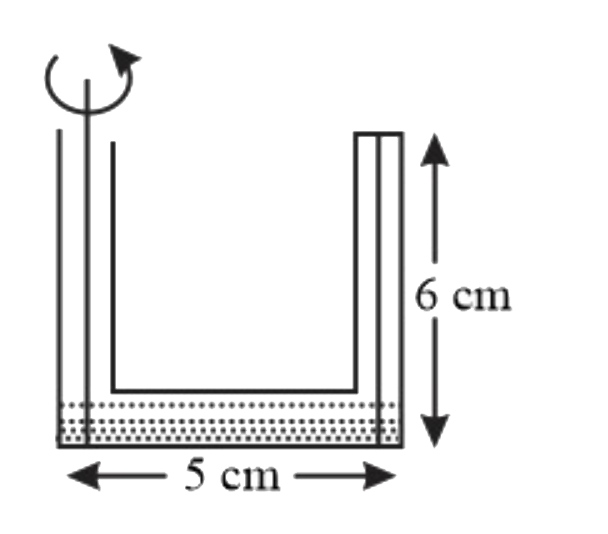
Length of the horizontal arm of a uniform cross - section U - tube is l = 5 cm and both ends of the vertical arms are open to the surrounding pressure of 7700 N m−2. A liquid of density ρ=103 kg m−3 is poured into the tube such that the liquid just fills the horizontal part of the tube. Now, one of the open ends is sealed and the tube. Now, one of the open ends is sealed and the tube is then rotaed about a vertical axis passing through the other veritcal arm with angular velocity ω due to which the liquid rises up to half the length of the vertical arm. If length of each vertical arm is a = 6 cm. What is the value of ω(in rad s−1)?
View SolutionA vertical U-tube has a liquid up to a height h. If the tube is slowly rotated to an angular speed ω=√gh find the (i) heights of the liquid column, ii pressures at the points 1,2 and 3 in the limbs in steady state.

View SolutionA rod of mass M and length l attached with a small bob of mass m at its end is freely rotating about a vertical axis passing through its other end with a constant angular speed ω. Find the force exerted by the system (rod and bob) on the pivot. Assume that gravity is absent.
View SolutionLength of a horizontal arm of ends of both the vertical arms pressure P0=105N/m2. A liquid of density ρ=103kg/m3 is poured in the tube such that liquid just fills the horizontal part of the tube as a shown in Fig. Now one end of the open ends is sealed and the tube is then rotated about a vertical axis passing through the other vertical arm with angular speed ω0=√40/3rad/sec. If length of each vertical arm is a=1m and in the sealed end liquid rises to a height y=1/2m, find pressure in the sealed tube during rotation. (in ×105N/m2)

View SolutionA small wedge whose base is horizontal is fixed to a vertical rod as shown in fig . The sloping side of the weidgeis frictionless and the wedge is span with a constant angular speed ω about vertical axis as shown in the fig find the
a. value of angular speed ω for which the block of mass m just does not slide down the wedge.
b. normal reaction on the block by wedge when block does not slip relative to wedge.

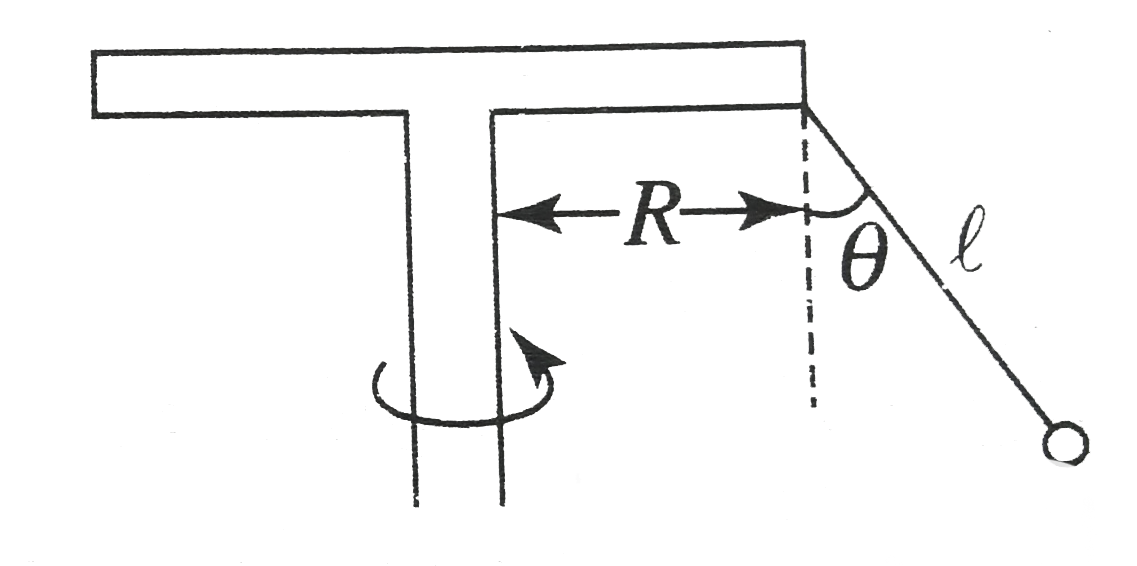
View SolutionA pendulum bob of mass m hangs from one end of a horizontal rod which is rotating about vertical axis with an unknown angular speed ω such that the light inextensible string of length l of the pedulum makes a constant angle θ with vertical. Find the
Q. angular speed ω
View SolutionLength of horizontal arm of a uniform cross section U-tube is l=21cm and ends of both of the vertical arms are open to surrounding of pressure 10500N/m2. A liquid of density ρ=103kg/m3 is poured into the tube such that liquid just fills the horizontal part of the tube. Now one of the open ends is sealed and the tube is then rotated about a vertical axis passing through the other vertical arm With angular velocity ω0=10rad/s. If length of each vertical arm is a=6cm, calculate the length of air column in the sealed arm. (in cm)

View SolutionA thin uniform rod of length l and mass m is swinging freely about a horizontal axis passing through its end. Its maximum angular speed is ω. Its centre of mass rises to a maximum height of -
View SolutionA horizontal thin tube of length 2L completely filled with a liquid of density δ rotates about a vertical axis passing through one of its end and along the diameter of its side face with an constant angular velocity ω. Two vertical thin long tubes are fitted with the horizontal tube to measure the pressure difference between points A and B which are at same horizontal level as shown. Neglect viscous forces and surfaces tension of liquid.

The difference in the heights (h) of the liquid column in the two vertical thin tubes is :
View SolutionA ring of radius r is rotating about a vertical axis along its diameter with constant angular velocity ω.A read of mass m remains at rest w.r.t. ring at the position shown in figure. Then w2 is:
_2019_CBT8_E01_015_Q01.png)
View Solution
