Oil enters the bend of a pipe in the horizontal plane with velocity and pressure as shown in the figure. Find the pressure of oil at the point in
(Take specific gravity of oil as 0.9 and )

The correct Answer is:
Let and be the cross sectional areas of the pipe at points and , respectively.
Let and be velocities of oil at the points and , respectively. By conservation of mass.
Applying Bernoulli's equation between points and we have
Topper's Solved these Questions
- FLUID MECHANICSBook:CENGAGE PHYSICS ENGLISHChapter:FLUID MECHANICSExercise:Single Correct
Explore 95 Videos
- FLUID MECHANICSBook:CENGAGE PHYSICS ENGLISHChapter:FLUID MECHANICSExercise:Multipe Correct
Explore 15 Videos
- FLUID MECHANICSBook:CENGAGE PHYSICS ENGLISHChapter:FLUID MECHANICSExercise:Exercise 4.4
Explore 10 Videos
- DIMENSIONS & MEASUREMENTBook:CENGAGE PHYSICS ENGLISHChapter:DIMENSIONS & MEASUREMENTExercise:Integer
Explore 2 Videos
- GRAVITATIONBook:CENGAGE PHYSICS ENGLISHChapter:GRAVITATIONExercise:INTEGER_TYPE
Explore 1 Video
Similar Questions
In the figure shown below, a fluid of density 2×103 kg m−3 is flowing in a horizontal pipe. The speed of water at point A is 4 cm s−1, what is its speed at point B?
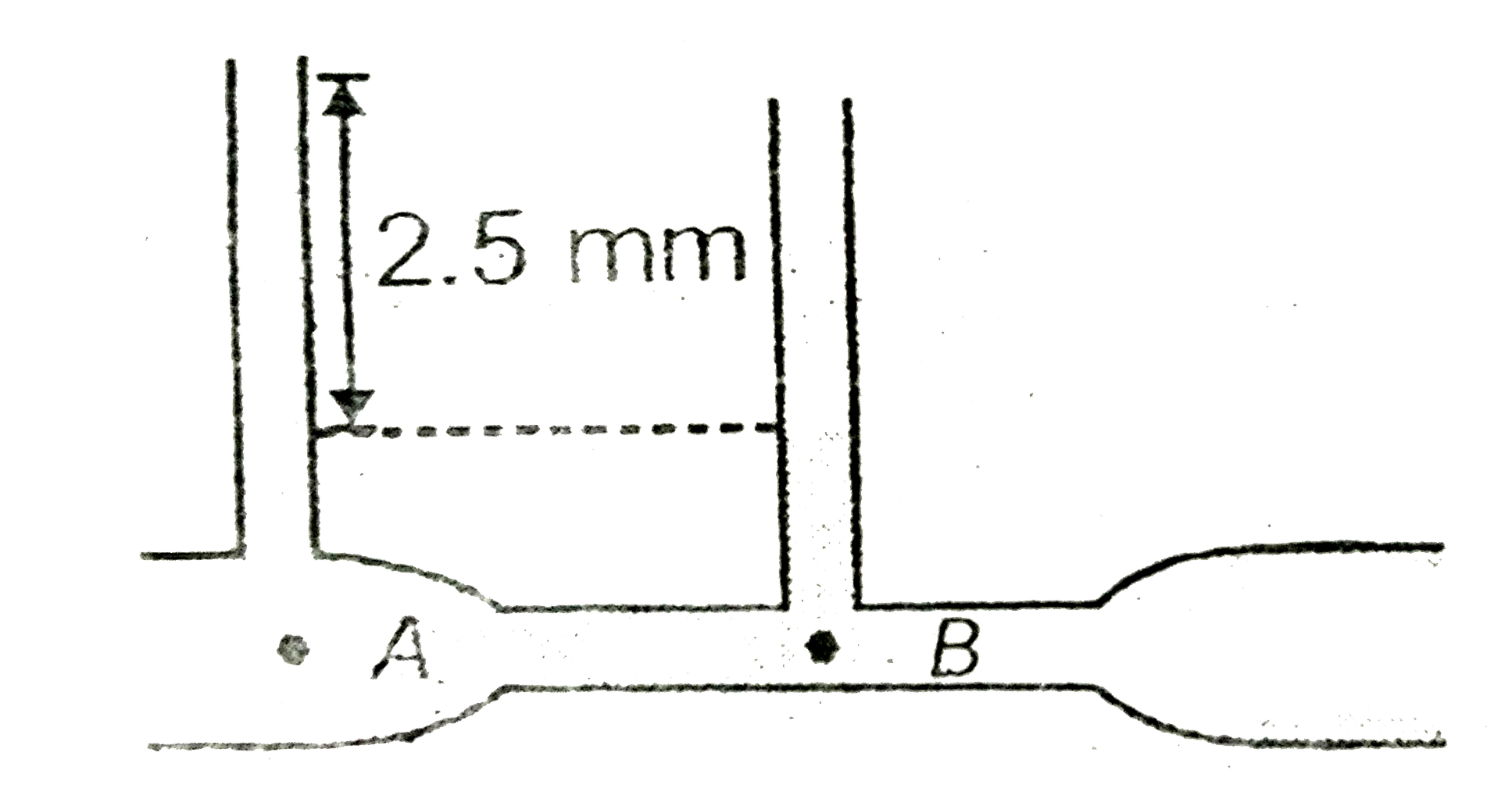
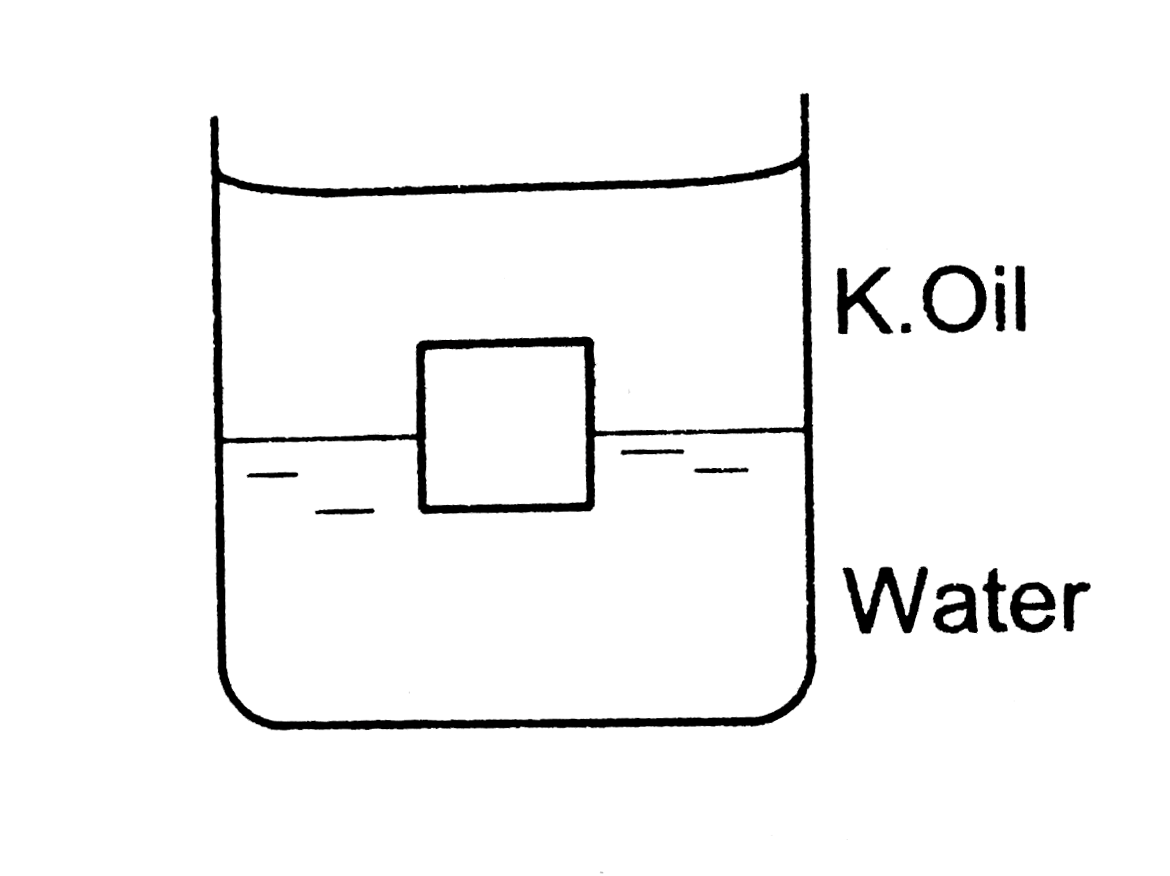
View SolutionA cube of ice floats partly in water and partly in K.oil figure. Find the ratio of the volume of ice immersed in water to that in K.oil. Specific gravity of K.oil is 0.8 and that of ice is 0.9.
View SolutionThe molecules of a given mass of a gas have rms velocity of 200msat27∘Cand1.0×105N/m2 pressure. When the temperature and pressure of the gas are respectively 127∘Cand0.05×105Nm−2, the rms velocity of its molecules in ms−1 is
(a) 400√3 (b) 100√23 (c) 1003 (d) 100√2
View SolutionThe reading of a pressure meter attached to a horizontal closed pipe is 3×105Nm−2. This reading falls to 1×105Nm−2 when the valve is opened. What is the speed of water flowing in the pipe?
View SolutionA sample of a given mass of gas at a constant temperature occupies 95cm3 under a pressure of 9.962×104Nm−2. At the same temperature its volume at a pressure of 10.13 xx 10^(4) Nm^(-2) is
View SolutionA particle moving with speed v0=10√2ms−1 strikes a wall at an angle 45∘ as shown in figure. Find magnitude of change in velocity.
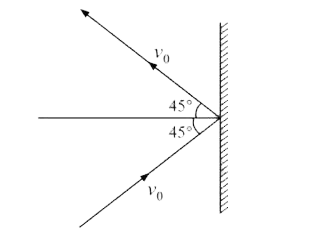
View SolutionA body is projected horizontally with a velocity of 4ms−1 from the top of a high tower. The velocity of the body after 0.7 is nearly (Take, g=10ms−2)
View SolutionWhat is the density of lead under a pressure of 2×108Nm−2 , if the bulk modulus of lead is 8×109Nm−2 and initially the density of lead is 11.4gcm−3 ?
View SolutionWhat is the density of lead under a pressure of 2×108Nm−2 , if the bulk modulus of lead is 8×109Nm−2 and initially the density of lead is 11.4gcm−3 ?
View SolutionA siphon tube is discharging a liquid of density
900kgm3 as shown in figure. (P0=1.01×105N/m2)

Pressure at point B is
View Solution