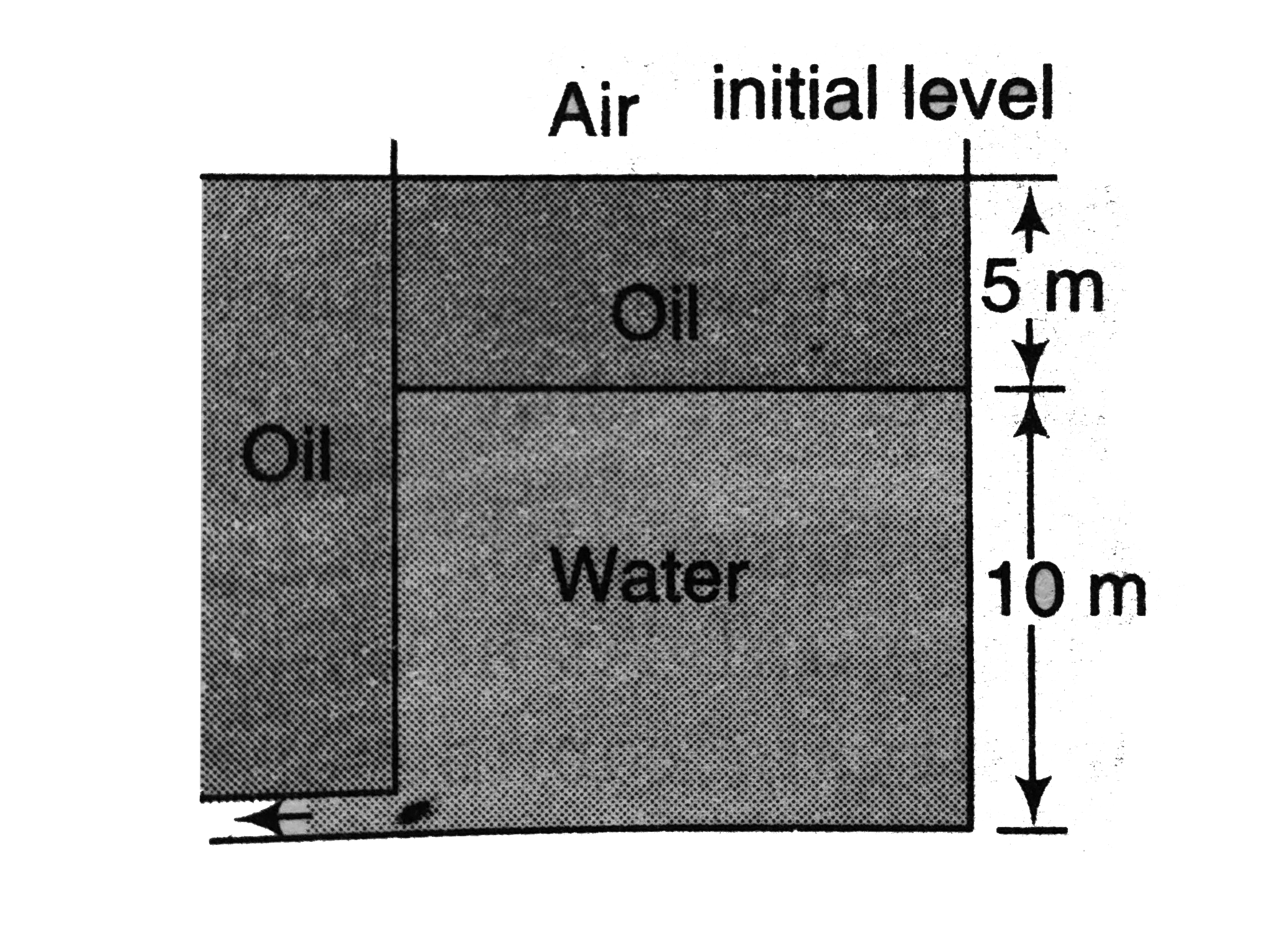
A tank having a small circular hole contains oil on top of water. It is immersed in a large tank of the same oil. Water flows through the hole. What is the velocity of the velocity of this flow initially? When the flow stops. What would be the position of the oil-water interface in the tank from the bottom. The specfic gravity of oil is 0.5.
The correct Answer is:t=√2/5s
Applying Bernoulli's equation just outside and just inside in orifice.
a. P0+ρoil(15)=12ρwV2=P0+ρwg(10)+ρoilg(15)
∴V=√40m/s=6.3m/s
b. Let h be the height when flow through orifice slopes. Again applying Bernoulli's equation
P0+ρoil(5)+ρwgh=P0+ρoil(15)
h=ρoilρw10=8m
c. P0+ρoil(5)ρωgh=P0+ρoil(15)+12ρωV2
∴V=√20(h−8)
⇒−dhdt=√20(h−8)⇒−∫810dh√(20(h−8))=∫t0dt
∴t=√25s
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - FLUID MECHANICSEXERCISE - Single Correct95videos
FLUID MECHANICS
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - FLUID MECHANICSEXERCISE - Multipe Correct15videos
FLUID MECHANICS
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - FLUID MECHANICSEXERCISE - Exercise 4.410videos
FLUID MECHANICS
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - DIMENSIONS & MEASUREMENTEXERCISE - Integer2videos
DIMENSIONS & MEASUREMENT
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - GRAVITATIONEXERCISE - INTEGER_TYPE1videos
GRAVITATION
Similar Questions
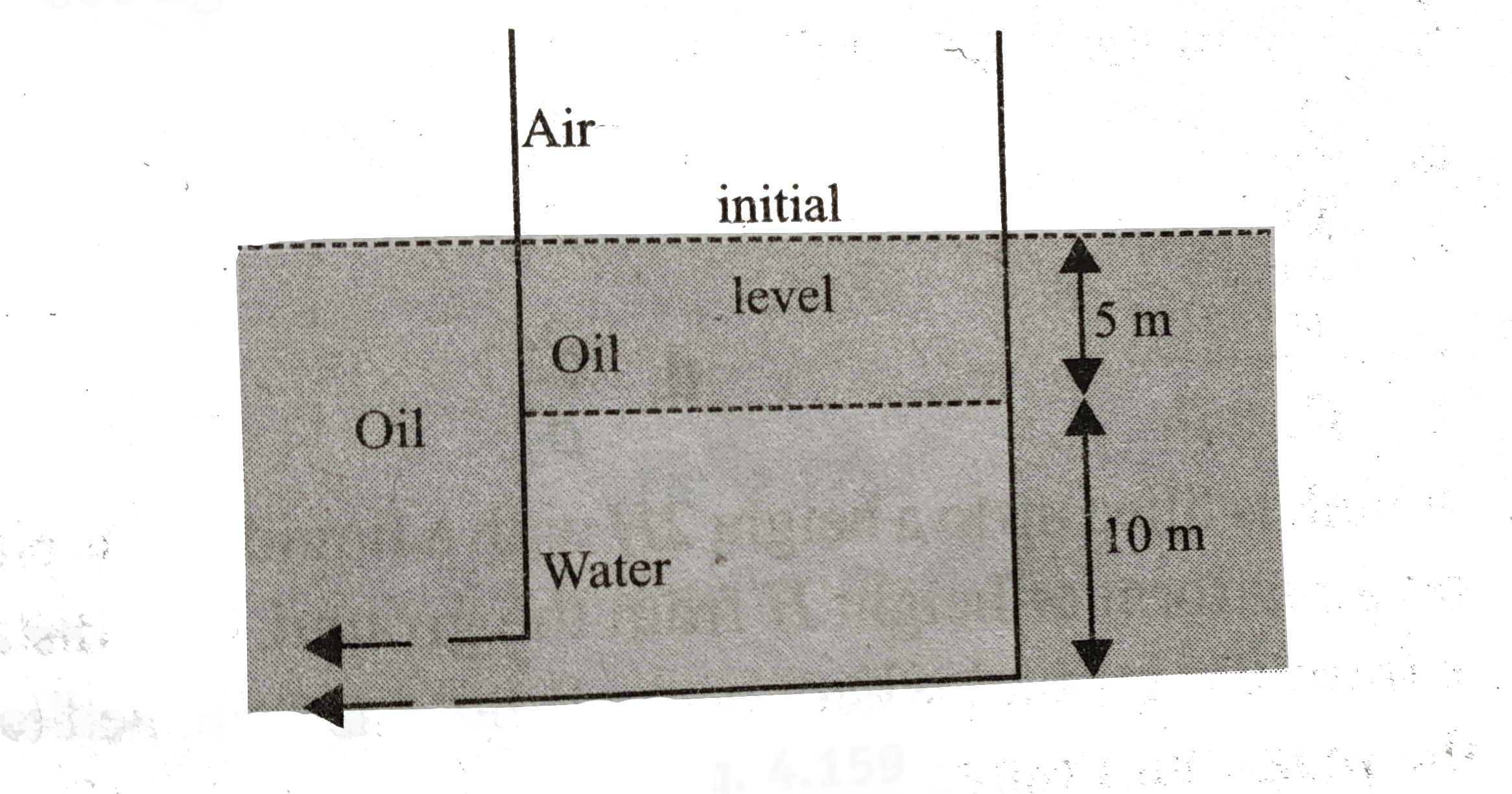
A tank with a small orifice contains oil on top of water. It is immersed in a large tank of the same oil. Water flows through the hole. Assuming the level of oil outside the tank above orifice does not change.
a. What is the velocity of this flow initially?
b. When the flow stops, what would be the position of the oil-water interface in the tank?
c. Determine the time at which the flow stops. Density,of oil 800kg/m3.
 View Solution
View SolutionA water tank has a hole at a distance of 7 m from free water surface. Find the velocity of water through the hole. If the radius of the hole is 2 mm what is the rate of flow of water?
View Solution
Knowledge Check
- Question 1 - Select One
A tank filled with fresh water has a hole in its bottom and water is flowing out of it. If the size of the hole is increased, then
Athe volume of water flowing out per second will decreaseBthe velocity of outflow of water remains unchangedCthe volume of water volume out per second remains zeroDBoth (b) and (c)
Water is flowing through a horizontal tube of non-uniform cross-section. At a place, the radius of the tube is 1.0cm and the velocity of water is 2m/s. What will be the velocity of water where the radius of the pipe is 2.0cm?
View SolutionA cylindrical tank whose cross-section area is 2000cm2 has a hole in its bottom 1cm2 in area.
(i) If the water is allowed to flow into the tank from a tube above it at the rate of 140 cm3/s, how high will the water in the tank rise ?
(ii) If the flow of water into the tank is stopped after the above height has been reached, how long will it take for tank to empty itself through the hole?View SolutionWater flows into a large tank with flat bottom at the rate of 10−4m3s−1. Water is also leaking out of a hole of area 1 cm2 at its bottom. If the height of the water in the tank remains steady, then this height is :
View SolutionA large tank filled with water to a height h is to be emptied through a small hole at the bottom. The ratio of times taken for the level of water to fall from h to h2 and from h2 to zero is
View SolutionWater flows through a horizontal pipe of varying area of cross-section at the rate 5 cubic metre per minute. What is the velocity of water at a point where pipe radius is 10 cm?
View SolutionA area of cross section of a large tank is 0.5m2. It has an opening near the bottom having area of cross section 1cm2. A load of 20 kg is applied on the water at the top. Find the velocity of the water coming out of the opening at the time when the height of water level is 50 cm above the bottom. Take g=10ms−2
View SolutionA area of cross section of a large tank is 0.5m2. It has an opening near the bottom having area of cross section 1cm2. A load of 20 kg is applied on the water at the top. Find the velocity of the water coming out of the opening at the time when the height of water level is 50 cm above the bottom. Take g=10ms−2
View Solution
