A rod of mass M and length l attached with a small bob of mass m at its end is freely rotating about a vertical axis passing through its other end with a constant angular speed ω. Find the force exerted by the system (rod and bob) on the pivot. Assume that gravity is absent.
To solve the problem, we need to find the total force exerted by the rod and bob system on the pivot when the system is rotating with a constant angular speed ω and gravity is absent.
1. Identify the Forces Acting on the Rod:
The rod is rotating about a vertical axis, and due to this rotation, each segment of the rod experiences a centrifugal force. We will calculate the total centrifugal force acting on the rod.
2. Consider an Element of the Rod:
Take an infinitesimal segment of the rod of length dr at a distance r from the pivot. The mass of this segment can be expressed as:
dm=Ml⋅dr
where M is the mass of the rod and l is its length.
3. Calculate the Centrifugal Force on the Element:
The centrifugal force dF acting on this segment due to rotation is given by:
dF=ω2⋅r⋅dm=ω2⋅r⋅(Ml⋅dr)
4. Integrate to Find Total Centrifugal Force on the Rod:
To find the total centrifugal force F acting on the entire rod, integrate dF from 0 to l:
F=∫l0dF=∫l0ω2⋅r⋅(Ml⋅dr)=Mω2l∫l0rdr
The integral ∫l0rdr evaluates to l22:
F=Mω2l⋅l22=Mω2l2
5. Calculate the Force Exerted by the Bob:
The bob of mass m is at a distance l from the pivot. The centrifugal force F′ acting on the bob is given by:
F′=m⋅ω2⋅l
6. Total Force Exerted on the Pivot:
The total force Ft exerted by the system on the pivot is the sum of the forces due to the rod and the bob:
Ft=F+F′=Mω2l2+m⋅ω2⋅l
Simplifying this gives:
Ft=(M2+m)ω2l
Final Answer:
The total force exerted by the system (rod and bob) on the pivot is:
Ft=(M2+m)ω2l
The rod is rotating about a vertical axis, and due to this rotation, each segment of the rod experiences a centrifugal force. We will calculate the total centrifugal force acting on the rod.
Take an infinitesimal segment of the rod of length dr at a distance r from the pivot. The mass of this segment can be expressed as:
dm=Ml⋅dr
where M is the mass of the rod and l is its length.
The centrifugal force dF acting on this segment due to rotation is given by:
dF=ω2⋅r⋅dm=ω2⋅r⋅(Ml⋅dr)
To find the total centrifugal force F acting on the entire rod, integrate dF from 0 to l:
F=∫l0dF=∫l0ω2⋅r⋅(Ml⋅dr)=Mω2l∫l0rdr
The integral ∫l0rdr evaluates to l22:
F=Mω2l⋅l22=Mω2l2
The bob of mass m is at a distance l from the pivot. The centrifugal force F′ acting on the bob is given by:
F′=m⋅ω2⋅l
The total force Ft exerted by the system on the pivot is the sum of the forces due to the rod and the bob:
Ft=F+F′=Mω2l2+m⋅ω2⋅l
Simplifying this gives:
Ft=(M2+m)ω2l
The total force exerted by the system (rod and bob) on the pivot is:
Ft=(M2+m)ω2l
Similar Questions
A uniform rod of length l, mass m, cross-sectional area A and Young's modulus Y is rotated in horizontal plane about a fixed vertical axis passing through one end, with a constant angular velocity ω. Find the total extension in the rod due to the tension produced in the rod.
View SolutionA uniform rod of mass m and length l rotates in a horizontal plane with an angular velocity ω about a vertical axis passing through one end. The tension in the rod at a distance x from the axis is
View SolutionA thin uniform rod of length l and mass m is swinging freely about a horizontal axis passing through its end. Its maximum angular speed is ω. Its centre of mass rises to a maximum height of -
View SolutionA uniform rod of mass m and length l0 is rotating with a constant angular speed ω about a vertical axis passing through its point of suspension. Find the moment of inertia of the rod about the axis of rotation if it make an angle θ to the vertical (axis of rotation).
View SolutionThe moment of inertia of a straight thin rod of mass M and length l about an axis perpendicular to its length and passing through its one end, is
View SolutionTwo identical small balls are suspended by ends of a rod. Whole assembly is rotating about vertical axis passing through center of rod. At a certain value of ω both strings make 37° with vertical. Find ω
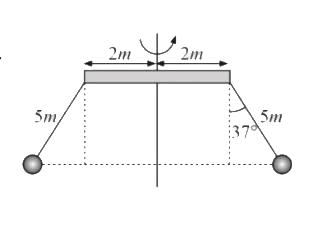
View SolutionTwo identical small balls are suspended by ends of a rod. Whole assembly is rotating about vertical axis passing through center of rod. At a certain value of ω both strings make 37° with vertical. Find ω

View SolutionConsider a uniform rod of mass m and length 2l with two particles of mass m each at its ends. Let AB be a line perpendicular to the length of rod and passing through its centre. Find the moment of inertia of the system about AB.
View SolutionA rod AB of mass m and length L is rotating in horizontal plane about one of its ends which is pivoted. The constant angular speed with which the rod is rotating is ω. The force applied on the rod by the pivot is
View SolutionA uniform rod of mass m and length L is free to rotate in the vertical plane about a horizontal axis passing through its end. The rod initially in horizontal position is released. The initial angular acceleration of the rod is:

View Solution
