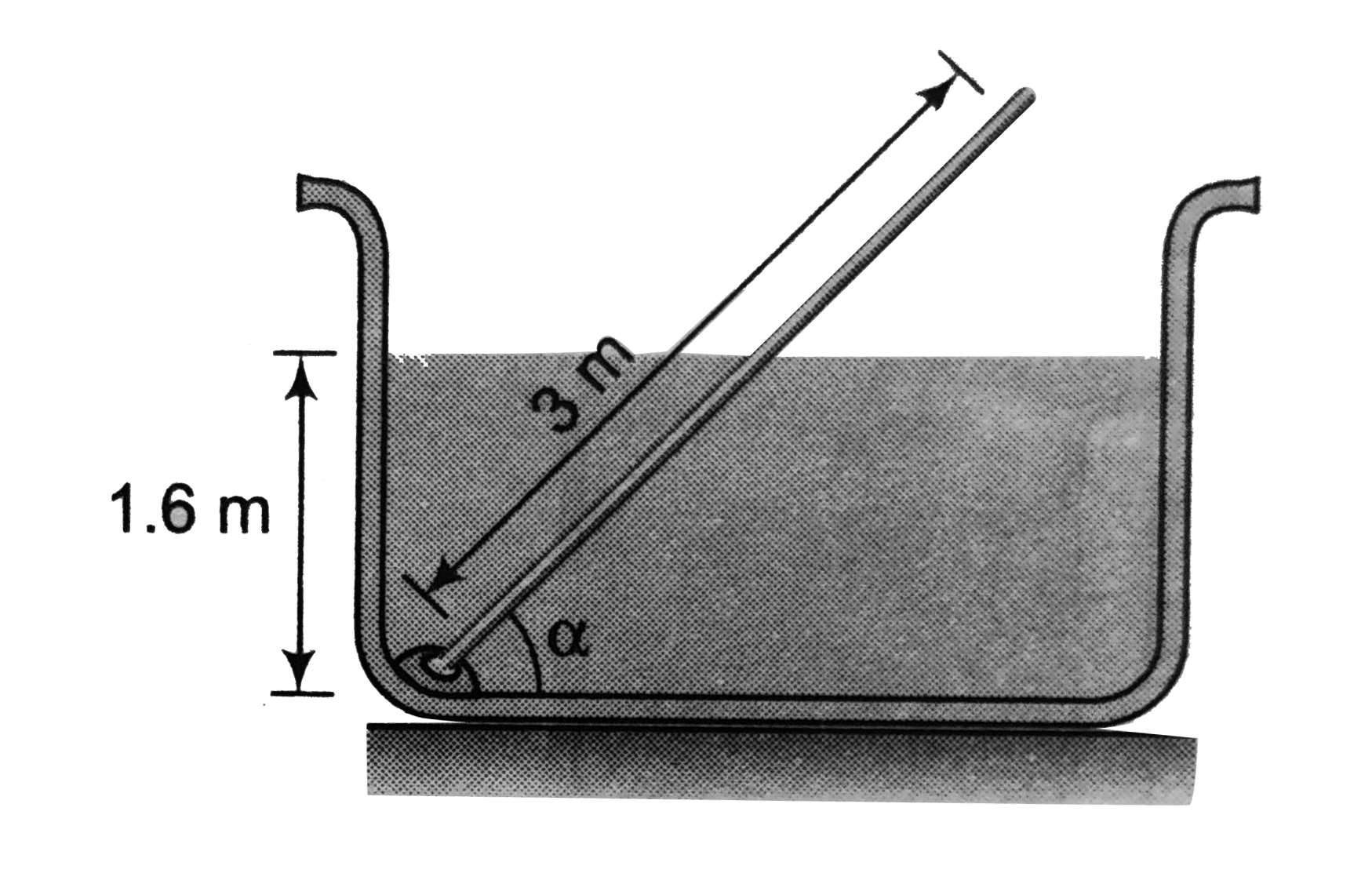
A wooden rod weighing 25N is mounted on a hinge below the free surface of water as shown. The rod is 3m long and uniform in cross section and the support is 1.6m below the free surface. At what angle α rod is in equilibrium? The cross-section of the rod is 9.5×10−4m2 in area. Density of water is 1000kg/m3. Assume buoyancy to act at centre of immersion. g=9.8m/s2. Also find reaction on the hinge in this position.
 .
.
The correct Answer is:A, C, D
Let G be the mid-point of AB and E the mid point of AC(i.e. the centre of buoyancy)

AC=1.6cosecα
Volume of AC
(1.6×9.5×10−4)cosec(α)
Weight of water displaced by AC
=(1.6×9.5×10−4)cosecα
=14.896cosecα
Hence, the buoyant force is 14.896cosedα vertically upwards atE. While the weight of the rod is 25N acting vertically downwards at G. Taking moments about A.
(14.896cosecα)(AEcosα)=(25)(AGcosα)
or, (14.896cosecα)(1.6cosecα2)=25×32
or, sin2α=0.32
∴sinα=0.56
or. α=34.3∘
Further. LetF be the reaction at hinge in vertically downward direction. Then, considering the tranlatory equilibrium of in vertical direction we have,
F+weight of the rod=upthrust
F=upthrust -weight of the rod
=14.896cosec(34.3∘)−25
=26.6−25
∴F=1.6N.
Topper's Solved these Questions
- FLUID MECHANICSBOOK - DC PANDEY ENGLISHCHAPTER - FLUID MECHANICSEXERCISE - Exercise16.1
6 Videos
- FLUID MECHANICSBOOK - DC PANDEY ENGLISHCHAPTER - FLUID MECHANICSEXERCISE - Introductory Exercise
1 Video
- FLUID MECHANICSBOOK - DC PANDEY ENGLISHCHAPTER - FLUID MECHANICSEXERCISE - Solved Examples
21 Videos
- EXPERIMENTSBOOK - DC PANDEY ENGLISHCHAPTER - EXPERIMENTSEXERCISE - Subjective
15 Videos
- GENERAL PHYSICSBOOK - DC PANDEY ENGLISHCHAPTER - GENERAL PHYSICSEXERCISE - INTEGER_TYPE
2 Videos
Similar Questions
At what depth below the surface of water will pressure be equal to twice the atmospheric pressure ? The atmospheric pressure is 10Ncm−2 , density of water is 103kgm−3 and g=9.8ms−2.
View SolutionA uniform rod of mass M and length L, area of cross section A is placed on a smooth horizontal surface. Forces acting on the rod are shown in the digram

Total elastic potential energy stored in the rod is :
View SolutionA horizontal pipeline carries water in a streamline flow. At a point along the tube where the cross sectional area is 10−2(m2), the water velcity is 2m/s and the pressure is 8000Pa. The pressure of water at another point where cross sectional area is 0.5×(10)−2(m2) is
View SolutionThree rods of uniform area of cross section A=10−7m2 are arranged as shown in Fig. Find out the shift in point B,C and D.

View SolutionThe thin rod shown below has mases M and length L. A force F acts at one end as shown and the rod is free to rotate about the other end in horizontal plane. Initial angular acceleration of the rod is :

View SolutionCalculate the apprroximate change in density of water in a lake at a depth of 400m below the surface. The density of water at the surface id 1030kg/m3 and bulk modulus of water is 2×109N/m2.
View SolutionCalculate the apprroximate change in density of water in a lake at a depth of 400m below the surface. The density of water at the surface id 1030kg/m3 and bulk modulus of water is 2×109N/m2.
View SolutionWater is flowing steadily through a horizontal pipe of non - uniform cross - section . If the velocity of water cross - section is 0.02m2 is 2m/s , what is the velocity of water at another point where the cross - section is 0.01m2 ?
View SolutionTwo blocks A and B of masses m and 2m are placed on a smooth horizontal surface. Block B is given a speed of 3m/s. Find
(i) The maximum speed of A
(ii) The minimum speed of B.
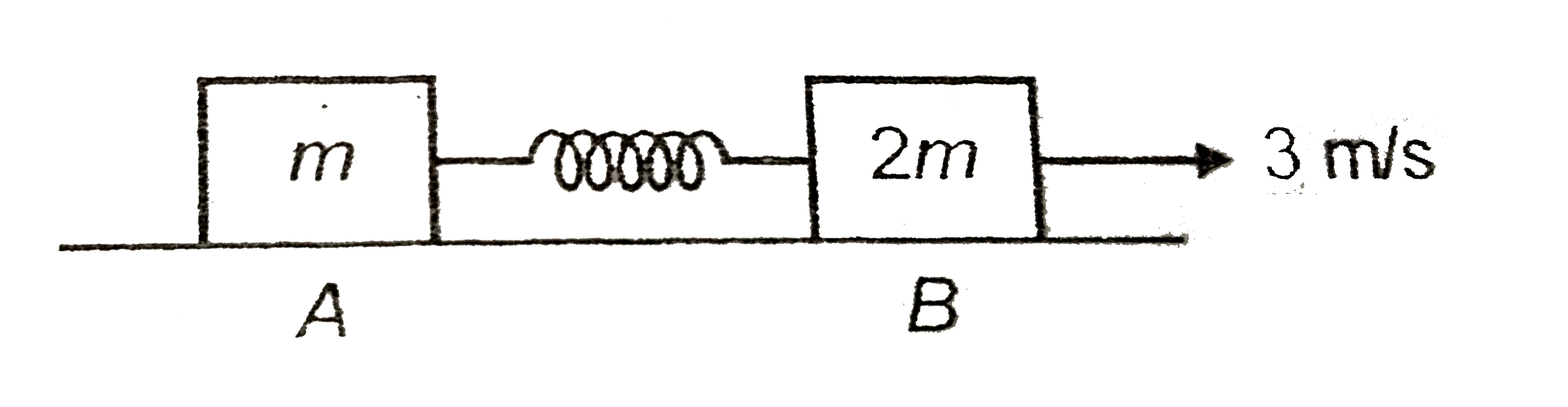
View SolutionA wooden rod of a uniform cross section and of length 120cm is hinged at the bottom of the tank which is filled with water to a height of 40cm. In the equilibrium position, the rod makes an angle of 60∘ with the vertical. The centre of buoyancy is located on the rod at a distance (from the hinge) of
View Solution
