A wooden rod of a uniform cross section and of length 120cm is hinged at the bottom of the tank which is filled with water to a height of 40cm. In the equilibrium position, the rod makes an angle of 60∘ with the vertical. The centre of buoyancy is located on the rod at a distance (from the hinge) of
20cm
40cm
60cm
75cm
The correct Answer is:B
To solve the problem, we need to find the distance from the hinge to the center of buoyancy of the wooden rod submerged in water. Here’s a step-by-step solution:
Step 1: Understand the Problem
We have a wooden rod of length 120 cm hinged at the bottom of a tank filled with water to a height of 40 cm. The rod makes an angle of 60° with the vertical in its equilibrium position. We need to find the distance from the hinge to the center of buoyancy of the submerged part of the rod.
Step 2: Determine the Submerged Length of the Rod
Since the rod is at an angle of 60° with the vertical, we can use trigonometry to find out how much of the rod is submerged in water.
- The vertical height of the rod submerged in water can be calculated using:
h=L⋅cos(θ)
where L is the length of the rod (120 cm) and θ is the angle with the vertical (60°).
Step 3: Calculate the Submerged Length
Using the formula:
h=120⋅cos(60°)
Since cos(60°)=12:
h=120⋅12=60 cm
This means that the rod extends 60 cm vertically downwards from the hinge.
Step 4: Determine the Effective Submerged Length
However, the water level is only 40 cm high. Therefore, the actual submerged length of the rod is limited to the water height:
- The submerged length of the rod is 40 cm.
Step 5: Find the Center of Buoyancy
The center of buoyancy is located at the center of the submerged part of the rod. Since the submerged part is 40 cm long, the center of buoyancy will be at half of this length:
Center of Buoyancy=40 cm2=20 cm
Step 6: Calculate the Distance from the Hinge
Since the hinge is at the bottom of the rod, the distance from the hinge to the center of buoyancy is:
Distance from hinge=20 cm
Final Answer
Thus, the center of buoyancy is located at a distance of 20 cm from the hinge.
---
We have a wooden rod of length 120 cm hinged at the bottom of a tank filled with water to a height of 40 cm. The rod makes an angle of 60° with the vertical in its equilibrium position. We need to find the distance from the hinge to the center of buoyancy of the submerged part of the rod.
Since the rod is at an angle of 60° with the vertical, we can use trigonometry to find out how much of the rod is submerged in water.
h=L⋅cos(θ)
where L is the length of the rod (120 cm) and θ is the angle with the vertical (60°).
Using the formula:
h=120⋅cos(60°)
Since cos(60°)=12:
h=120⋅12=60 cm
This means that the rod extends 60 cm vertically downwards from the hinge.
However, the water level is only 40 cm high. Therefore, the actual submerged length of the rod is limited to the water height:
- The submerged length of the rod is 40 cm.
The center of buoyancy is located at the center of the submerged part of the rod. Since the submerged part is 40 cm long, the center of buoyancy will be at half of this length:
Center of Buoyancy=40 cm2=20 cm
Since the hinge is at the bottom of the rod, the distance from the hinge to the center of buoyancy is:
Distance from hinge=20 cm
Thus, the center of buoyancy is located at a distance of 20 cm from the hinge.
Topper's Solved these Questions
- FLUID MECHANICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - FLUID MECHANICSEXERCISE - Multipe Correct
15 Videos
- FLUID MECHANICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - FLUID MECHANICSEXERCISE - Assertion-Reasoning
8 Videos
- FLUID MECHANICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - FLUID MECHANICSEXERCISE - Subjective
25 Videos
- DIMENSIONS & MEASUREMENTBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - DIMENSIONS & MEASUREMENTEXERCISE - Integer
2 Videos
- GRAVITATIONBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - GRAVITATIONEXERCISE - INTEGER_TYPE
1 Video
Similar Questions
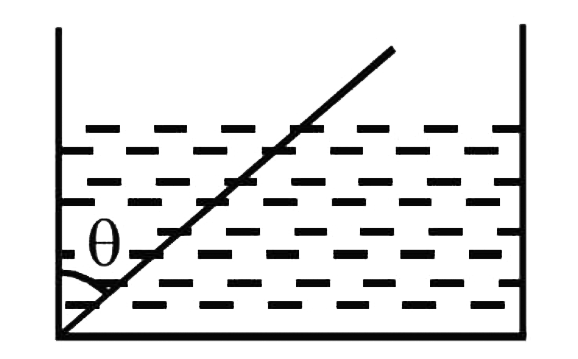
The wooden plank of length 1 m and uniform cross section is hinged at one end to the bottom of a tank as shown in figure. The tank is filled with water up to a height of 0.5 m. The specific gravity of the plank is 0.5. Find the angle θ that the plank makes with the vertical in the equilibrium position. (Exclude the case θ=0)
 ,
,
View SolutionA wooden plank of length 1m and uniform cross-section is hinged at one end to the bottom of a tank as shown in fig. The tank is filled with water upto a hight 0.5m. The specific gravity of the plank is 0.5. Find the angle θ that the plank makes with the vertical in the equilibrium position. (Exclude the case θ=θ∘)
View SolutionA rod of uniform cross-section of mass M and length L is hinged about an end to swing freely in a vertical plane. Howerver, its density is non uniform and varies linearly from hinged end to the free end doubling its value. The moment of inertia of the rod, about the rotation axis passing through the hinge point
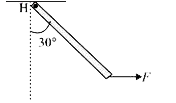
View SolutionA rod of mass m and length L is hinged at its top end. If the rod is in equilibrium making an angle of 30∘ with the vertical when a horizontal force F is applied as shown in figure, then the value of F is:
View SolutionA small wooden rod of length 5mm is fixed at the bottom of the container filled with water (μwater=43). It is making an angle 37∘ with vertical. If an observer (in air) observes the rod paraxially, and the rod is appearing at an angle πx radian with vertical then the find the value of x.

View SolutionA rod of mass m and length L is pivoted at the bottommost point O and can freely rotate about the point O. The rod is disturbed from the vertical position so that it starts rotating about O. When it makes an angle θ with the vertical
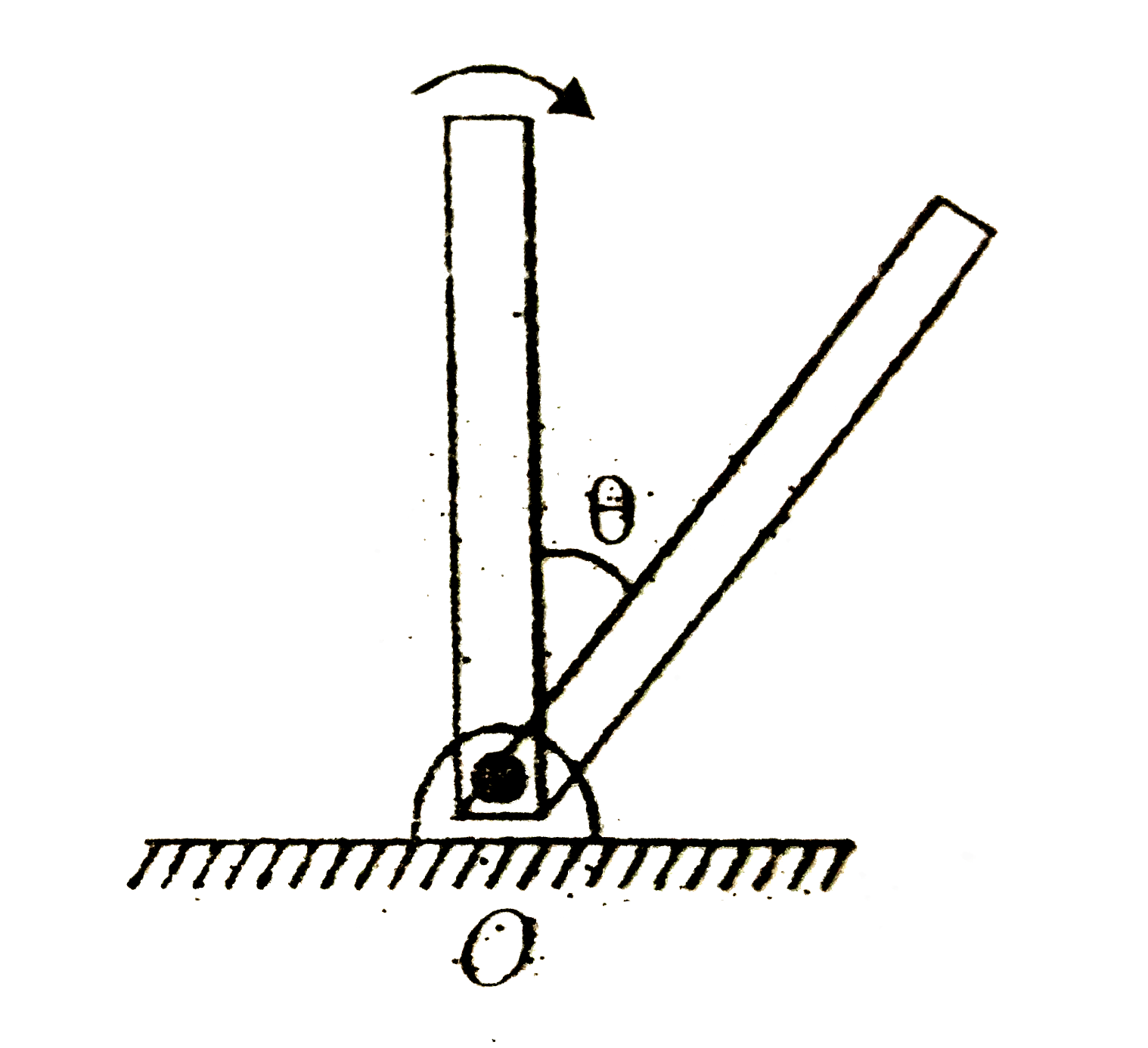
View SolutionA uniform thin rod of length l and mass m is hinged at a distance l/4 from one of the end and released from horizontal position as shown in Fig. The angular velocity of the rod as it passes the vertical position is

View SolutionA rod of length 10 meter has one end on smooth floor and the other end on smooth wall is released from the rest the position shown in figure. When the rod makes an angle of 37∘ with the horizontal, answer the following:

The velocity of centre of mass of rod is :
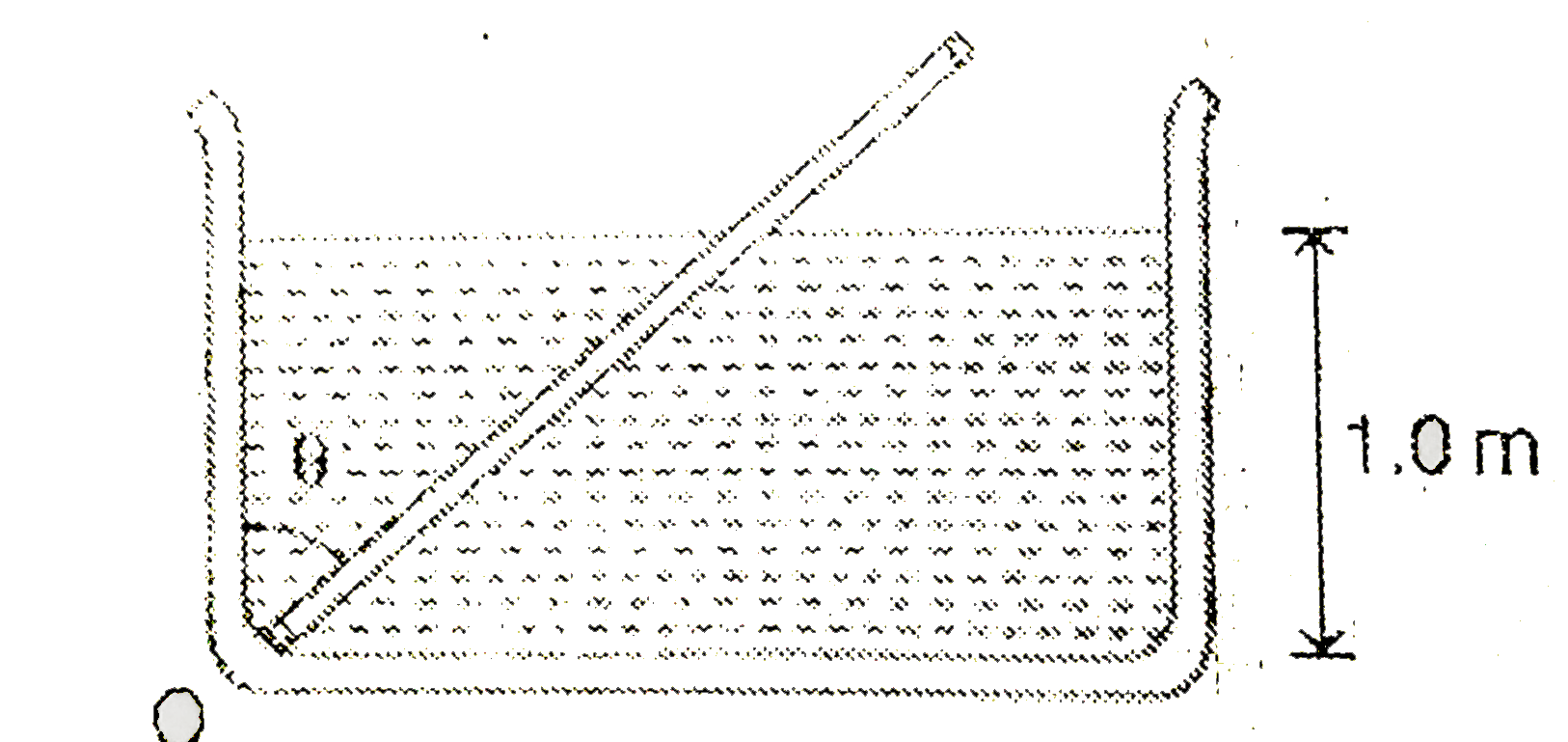
View SolutionA uniform rod of length 2.0 m specific gravity 0.5 and mass 2 kg is hinged at one end to the bottom of a tank of water (specific gravity = 10) filled upto a height o f 1.0 m as shown in figure. Taking the case θ=−0∘ the force exerted by the hings on the rod is (g=10m/s2)
View SolutionA uniform rod of length L pivoted at the bottom of a pond of depth L/2 stays in stable equilibrium as shown in the figure.

Find the angle 0 if the density of the material of the rod is half of the density of water.
View Solution
