At what depth below the surface of water will pressure be equal to twice the atmospheric pressure ? The atmospheric pressure is 10Ncm−2 , density of water is 103kgm−3 and g=9.8ms−2.
To find the depth below the surface of water at which the pressure is equal to twice the atmospheric pressure, we can follow these steps:
Step 1: Understand the given values
- Atmospheric pressure, Patm=10N/cm2
- Convert this to SI units (N/m² or Pascals):
Patm=10N/cm2=10×104N/m2=105N/m2
- Density of water, ρ=1000kg/m3
- Gravitational acceleration, g=9.8m/s2
Step 2: Set up the equation for pressure at depth
The total pressure at depth h in a fluid is given by:
P=Patm+ρgh
We want the total pressure to be twice the atmospheric pressure:
P=2Patm=2×105N/m2=2×105N/m2
Step 3: Substitute the values into the equation
Now, we can set up the equation:
2×105=105+ρgh
Substituting the known values:
2×105=105+(1000kg/m3)(9.8m/s2)h
Step 4: Simplify the equation
Rearranging the equation gives:
2×105−105=(1000)(9.8)h
105=9800h
Step 5: Solve for h
Now, divide both sides by 9800 to find h:
h=1059800
Calculating this gives:
h≈10.204m
Final Answer
Thus, the depth below the surface of water at which the pressure is equal to twice the atmospheric pressure is approximately:
h≈10.2m
---
- Atmospheric pressure, Patm=10N/cm2
- Convert this to SI units (N/m² or Pascals):
Patm=10N/cm2=10×104N/m2=105N/m2
- Density of water, ρ=1000kg/m3
- Gravitational acceleration, g=9.8m/s2
The total pressure at depth h in a fluid is given by:
P=Patm+ρgh
We want the total pressure to be twice the atmospheric pressure:
P=2Patm=2×105N/m2=2×105N/m2
Now, we can set up the equation:
2×105=105+ρgh
Substituting the known values:
2×105=105+(1000kg/m3)(9.8m/s2)h
Rearranging the equation gives:
2×105−105=(1000)(9.8)h
105=9800h
Now, divide both sides by 9800 to find h:
h=1059800
Calculating this gives:
h≈10.204m
Thus, the depth below the surface of water at which the pressure is equal to twice the atmospheric pressure is approximately:
h≈10.2m
Topper's Solved these Questions
- PRESSURE IN FLUIDS AND ATMOSPHERIC PRESSUREBook:ICSEChapter:PRESSURE IN FLUIDS AND ATMOSPHERIC PRESSUREExercise:Exercise-4(A)
Explore 31 Videos
- PRESSURE IN FLUIDS AND ATMOSPHERIC PRESSUREBook:ICSEChapter:PRESSURE IN FLUIDS AND ATMOSPHERIC PRESSUREExercise:Exercise-4(A)multiple choice
Explore 4 Videos
- MOTION IN ONE DIMENSION Book:ICSEChapter:MOTION IN ONE DIMENSION Exercise:EXERCISE -2 (C) ( Multiple choice type :)
Explore 17 Videos
- PROPAGATION OF SOUND WAVES Book:ICSEChapter:PROPAGATION OF SOUND WAVES Exercise:EXERCISE -8(B) (Multiple choice type)
Explore 3 Videos
Similar Questions
Knowledge Check
The pressure at depth h below the surface of a liquid of density ρ open to the atmosphere is
Agreater than the atmospheric pressure by ρghBless than the atmospheric pressure by ρghCequal to the atmospheric pressureDincreases exponentially with depth
The lower end of a capillary tube of diameter 2.0 mm is dipped 8.00cm below the surface of water in a beaker. What is the pressure required in the tube in order to blow a hemispherical bubble at its end in water? The surface tension of water at temperature of the experiments is 7.30×10−2Nm−1. 1 atmospheric pressure =1.01×105Pa, density of water =1000kg/m3,g=9.80ms−2. also calculate the excess pressure.
View SolutionFind the pressure exerted below a column of water, open to the atmosphere, at depth
(i) 5 m
(ii) 20 m
(Given, density of water = 1×103kg m−3,g=10ms−2)
View SolutionA square plate of side 10 m is placed horizontally 1 m below the surface of water. The atmospheric pressure is 1.013×105Nm−2. Calculate the total thrust on the plate.
(Density of water ρ=103kgm−3,g=9.8ms−2)
View SolutionWhat is the absolute pressure on a swimmer 10m below the surface of a lake? Take atmospheric pressure 1×105N/m2
View SolutionAn air bubble of radius 1 mm is located at a depth of 20 cm below water level. The excess pressure inside the bubble above the atmospheric pressure is [Given, the surface tension of water is 0.075 Nm−1 and density is 1000 kg m−3]
View SolutionA glass full of water has a bottom of area 20cm2, top of area 20cm, height 20cm and volume half a litre.
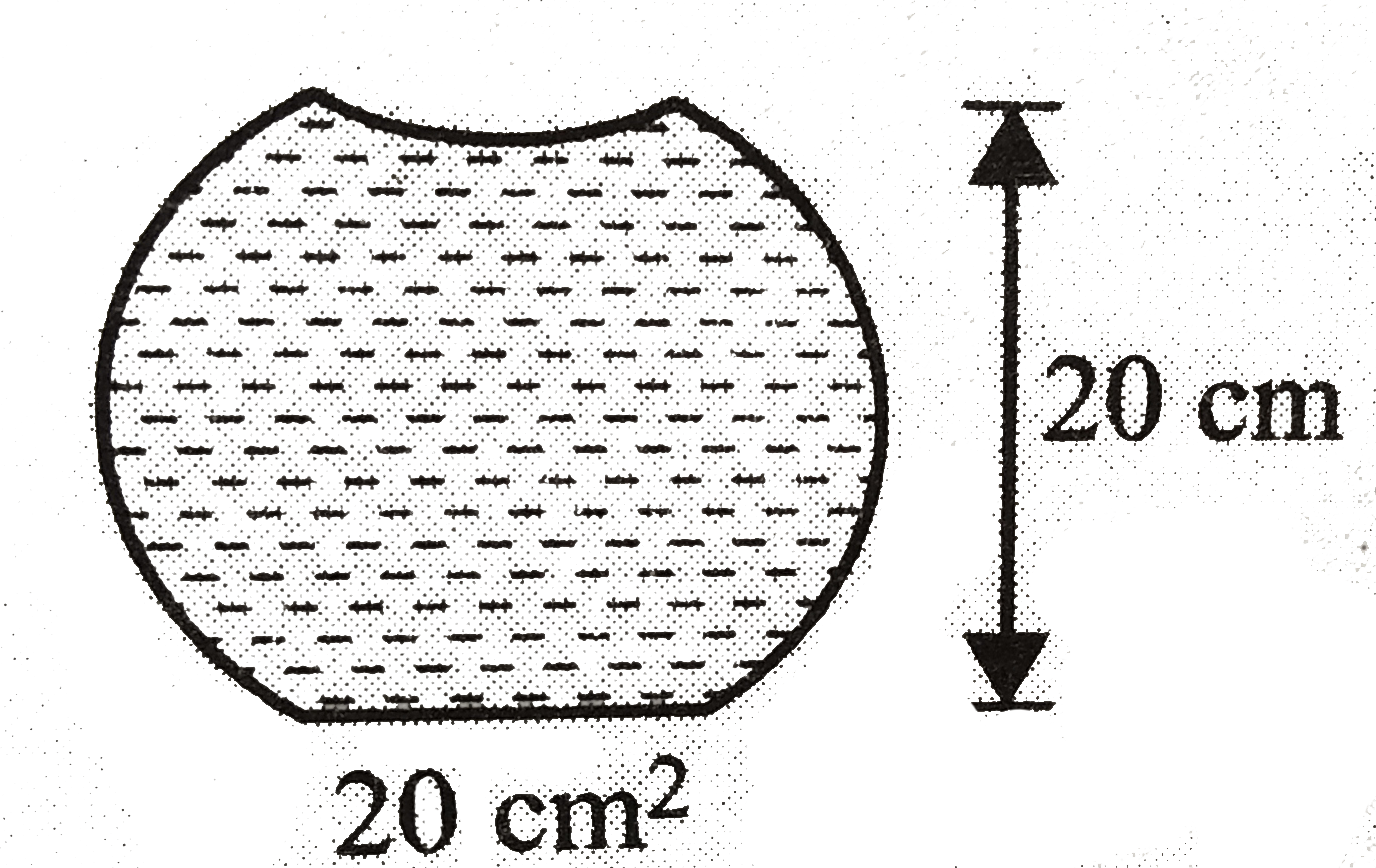
a. Find the force exerted by the water on the bottom.
b. Considering the equilibrium of the v, after. find the resultant force exerted by the side, of the glass on the water. Atmospheric pressure =1.0×105N/m2. Density of water =1000kg/m−3 and g=10m/s2
View SolutionThe pressure at a point in water is 10 N/m2. The depth below this point where the pressure becomes double is (Given density of water = 103 kg m−3, g = 10 m s−2)
View Solution

