Find the pressure exerted below a column of water, open to the atmosphere, at depth
(i) 5 m
(ii) 20 m
(Given, density of water = 1×103kg m−3,g=10ms−2)
To find the pressure exerted below a column of water at a given depth, we can use the hydrostatic pressure formula:
P=ρgh+P0
Where:
- P is the total pressure at depth,
- ρ is the density of the fluid (water in this case),
- g is the acceleration due to gravity,
- h is the depth of the fluid,
- P0 is the atmospheric pressure.
Given:
- Density of water, ρ=1×103kg/m3
- Acceleration due to gravity, g=10m/s2
- Atmospheric pressure, P0=1.01×105Pa
1. Calculate the hydrostatic pressure due to the water column:
Pwater=ρgh=(1×103kg/m3)(10m/s2)(5m)
Pwater=1×103×10×5=5×104Pa
2. Add atmospheric pressure:
P=Pwater+P0=5×104Pa+1.01×105Pa
P=5×104+1.01×105=1.51×105Pa
(ii) For depth h=20m:
1. Calculate the hydrostatic pressure due to the water column:
Pwater=ρgh=(1×103kg/m3)(10m/s2)(20m)
Pwater=1×103×10×20=2×105Pa
2. Add atmospheric pressure:
P=Pwater+P0=2×105Pa+1.01×105Pa
P=2×105+1.01×105=2.01×105Pa
Final Answers:
- Pressure at depth 5 m: P=1.51×105Pa
- Pressure at depth 20 m: P=2.01×105Pa
- P is the total pressure at depth,
- ρ is the density of the fluid (water in this case),
- g is the acceleration due to gravity,
- h is the depth of the fluid,
- P0 is the atmospheric pressure.
- Density of water, ρ=1×103kg/m3
- Acceleration due to gravity, g=10m/s2
- Atmospheric pressure, P0=1.01×105Pa
Pwater=ρgh=(1×103kg/m3)(10m/s2)(5m)
Pwater=1×103×10×5=5×104Pa
P=Pwater+P0=5×104Pa+1.01×105Pa
P=5×104+1.01×105=1.51×105Pa
Pwater=ρgh=(1×103kg/m3)(10m/s2)(20m)
Pwater=1×103×10×20=2×105Pa
P=Pwater+P0=2×105Pa+1.01×105Pa
P=2×105+1.01×105=2.01×105Pa
- Pressure at depth 5 m: P=1.51×105Pa
- Pressure at depth 20 m: P=2.01×105Pa
Topper's Solved these Questions
- MECHANICAL PROPERTIES OF FLUIDSBook:AAKASH INSTITUTE ENGLISHChapter:MECHANICAL PROPERTIES OF FLUIDSExercise:TRY YOURSELF
Explore 41 Videos
- MECHANICAL PROPERTIES OF FLUIDSBook:AAKASH INSTITUTE ENGLISHChapter:MECHANICAL PROPERTIES OF FLUIDSExercise:SECTION - A
Explore 50 Videos
- MAGNETISM AND MATTER Book:AAKASH INSTITUTE ENGLISHChapter:MAGNETISM AND MATTER Exercise:ASSIGNMENT (SECTION D)
Explore 26 Videos
- MECHANICAL PROPERTIES OF SOLIDSBook:AAKASH INSTITUTE ENGLISHChapter:MECHANICAL PROPERTIES OF SOLIDSExercise:Assignment(Section-D)
Explore 14 Videos
Similar Questions
Find the pressure exerted below a column of water, open to the atmosphere, at depth
(i) 10 m " " (ii) 30 m
(Given, density of water =1×103kgm−3,g=10ms−2)
View SolutionThe guage pressure exerted below a column of water, open to the earth's atmosphere at depth of 10 m is (density of water = 1000 kg/m3, g = 10 m/s2 and 1 atm pressure = 105 Pa)
View Solution
Knowledge Check
The force acting on a window of are 50×50 cm of a submarine at a depth of 2000 m in an ocean ,the interior of which is maintained at sea level atmospheric pressure is (density of sea water = 103kgm−3 ,g =10ms−2 )
A5×105NB25×105 NC5×106ND25×106N
The density of water is ........ kg/m3.
View SolutionThe pressure at a point in water is 10 N/m2. The depth below this point where the pressure becomes double is (Given density of water = 103 kg m−3, g = 10 m s−2)
View SolutionA glass full of water has a bottom of area 20cm2, top of area 20cm, height 20cm and volume half a litre.
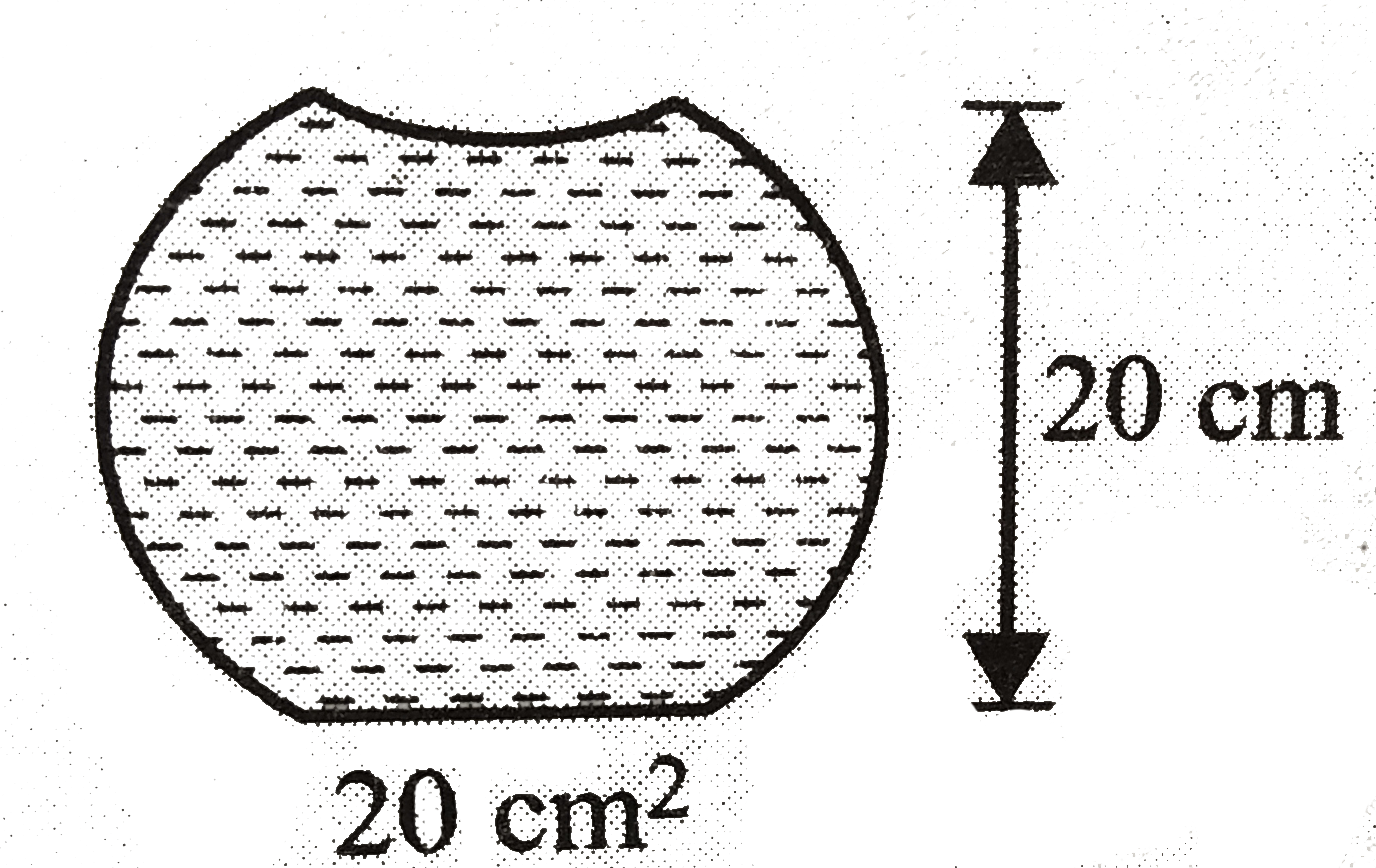
a. Find the force exerted by the water on the bottom.
b. Considering the equilibrium of the v, after. find the resultant force exerted by the side, of the glass on the water. Atmospheric pressure =1.0×105N/m2. Density of water =1000kg/m−3 and g=10m/s2
View SolutionAt what depth below the surface of water will pressure be equal to twice the atmospheric pressure ? The atmospheric pressure is 10Ncm−2 , density of water is 103kgm−3 and g=9.8ms−2.
View SolutionCalculate the pressure due to a water column of height 100 m. (Take g=10ms−2 and density of water =103kgm−3).
View SolutionThe pressure of water on the ground floor is 40,000 Pa and on the first floor is 10,000 Pa. Find the height of the first floor. (Take : density of water = 1000kg m−3,g=10m s−2 )
View SolutionA metallic sphere of radius 1.0×10−3m and density 1.0×104kg/m3 enters a tank of water, after a free fall through a distance of h in the earth's gravitational field. If its velocity remains unchanged after entering water, determine the value of h. Given: coefficient of viscosity of water =1.0×10−3Ns/m2,g=10ms−12 and density of water =1.0×103kg/m3.
View Solution

