Mercury of density ρm is poured into cylinderical communicating vessels of cross-sectional area 2A and A respectively. A solid iron cube of volume V0 and relative density 2 is dropped into the broad vessel, and as a result the level of the mercury in it rises. Then, water is poured into the broader vessel until the mercury reaches the previous level in it. Find the height of water column if it does not submerge the block.
To solve the problem step by step, we need to analyze the situation involving the communicating vessels, the iron cube, and the mercury and water levels.
Step 1: Understand the System
We have two communicating vessels with cross-sectional areas 2A and A. Mercury of density ρm is filled in both vessels. An iron cube with volume V0 and relative density 2 is dropped into the broader vessel (with area 2A).
Step 2: Calculate the Density of the Iron Cube
The density of the iron cube can be calculated using its relative density:
ρiron=2×ρwater
Assuming the density of water ρwater=1000kg/m3, we have:
ρiron=2×1000=2000kg/m3
Step 3: Determine the Volume of the Iron Cube
The volume of the iron cube is given as V0. The weight of the iron cube Wiron can be calculated as:
Wiron=ρiron×V0×g
where g is the acceleration due to gravity.
Step 4: Calculate the Rise in Mercury Level
When the iron cube is submerged in mercury, it displaces a volume of mercury equal to the volume of the cube. The rise in mercury level hm in the broader vessel can be determined by the equation:
Wiron=Weight of displaced mercury
ρiron×V0×g=ρm×(2A⋅hm)⋅g
Cancelling g from both sides, we get:
ρiron×V0=ρm×(2A⋅hm)
Rearranging gives:
hm=ρiron×V02A×ρm
Step 5: Pour Water into the Broader Vessel
After the iron cube is placed, water is poured into the broader vessel until the mercury returns to its original level. Let the height of the water column be hw. The volume of water poured in must equal the volume of mercury displaced:
A⋅hw=2A⋅hm
Thus, we can express hw as:
hw=2hm
Step 6: Substitute the Expression for hm
Substituting hm into the equation for hw:
hw=2⋅ρiron×V02A×ρm
This simplifies to:
hw=ρiron×V0A×ρm
Step 7: Final Calculation
Substituting ρiron=2000kg/m3:
hw=2000×V0A×ρm
Conclusion
The height of the water column hw in the broader vessel is given by:
hw=2000×V0A×ρm
We have two communicating vessels with cross-sectional areas 2A and A. Mercury of density ρm is filled in both vessels. An iron cube with volume V0 and relative density 2 is dropped into the broader vessel (with area 2A).
The density of the iron cube can be calculated using its relative density:
ρiron=2×ρwater
Assuming the density of water ρwater=1000kg/m3, we have:
ρiron=2×1000=2000kg/m3
The volume of the iron cube is given as V0. The weight of the iron cube Wiron can be calculated as:
Wiron=ρiron×V0×g
where g is the acceleration due to gravity.
When the iron cube is submerged in mercury, it displaces a volume of mercury equal to the volume of the cube. The rise in mercury level hm in the broader vessel can be determined by the equation:
Wiron=Weight of displaced mercury
ρiron×V0×g=ρm×(2A⋅hm)⋅g
Cancelling g from both sides, we get:
ρiron×V0=ρm×(2A⋅hm)
Rearranging gives:
hm=ρiron×V02A×ρm
After the iron cube is placed, water is poured into the broader vessel until the mercury returns to its original level. Let the height of the water column be hw. The volume of water poured in must equal the volume of mercury displaced:
A⋅hw=2A⋅hm
Thus, we can express hw as:
hw=2hm
Substituting hm into the equation for hw:
hw=2⋅ρiron×V02A×ρm
This simplifies to:
hw=ρiron×V0A×ρm
Substituting ρiron=2000kg/m3:
hw=2000×V0A×ρm
The height of the water column hw in the broader vessel is given by:
hw=2000×V0A×ρm
Topper's Solved these Questions
- MECHANICAL PROPERTIES OF FLUIDSBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - MECHANICAL PROPERTIES OF FLUIDSEXERCISE - SECTION - I
6 Videos
- MAGNETISM AND MATTER BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - MAGNETISM AND MATTER EXERCISE - ASSIGNMENT (SECTION D)
26 Videos
- MECHANICAL PROPERTIES OF SOLIDSBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - MECHANICAL PROPERTIES OF SOLIDSEXERCISE - Assignment(Section-D)
14 Videos
Similar Questions
The liquids shown in figure in the two arms are mercury (specific gravity =13.6) and water. If the difference of heights of the mercury columns is 2 cm, find the height of the water column.
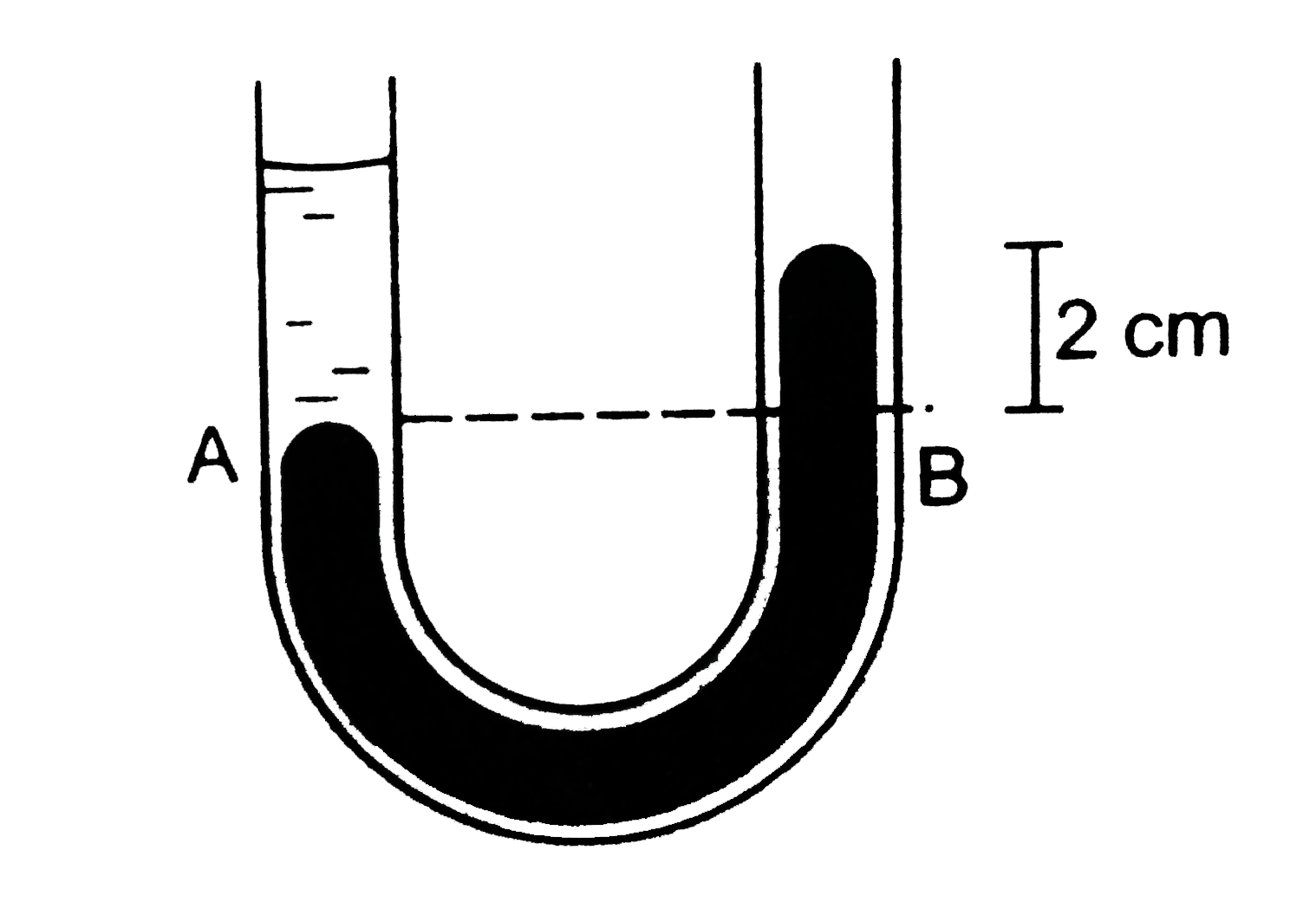 ,
,
View SolutionThe liquids shown in figure in the two arms are mercury (specific gravity =13.6) and water. If the difference of heights of the mercury columns is 2 cm, find the height of the water column.
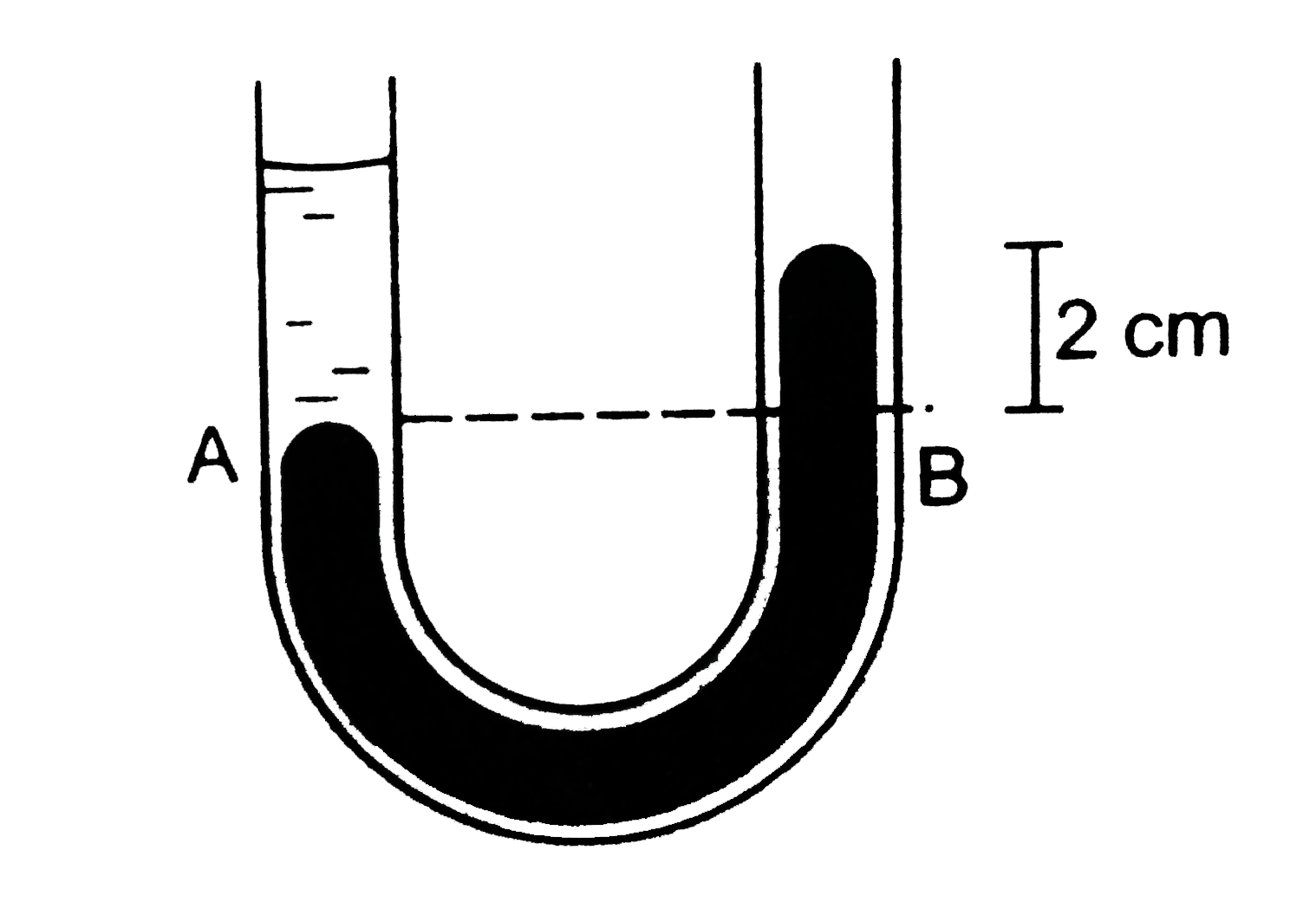 ,
,
View SolutionAn open U-tube contains mercury. When 11.2 cm of water is poured into one of the arms of the tube, how high does the mercury rise in the other arm from its initial level ?
View SolutionLymph vessels pour their materials in
View SolutionA conical vessel whose internal radius is 10 cm and height 48 cm is full of water. Find the volume of water. If this water is poured into a cylindrical vessel with internal radius 20 cm, find the height to which the water level rises in it.
View SolutionA cubical block of iron of side13.6cm is floating in mercury in a vessel .Water is poured in the vessel until it just covers the iron block. What is the height of water column? (ρHg=13.6gmcm3, ρFe=7.2gmcm3, ρH_2O=1gmcm3)
View SolutionA cubical metal block of edge 12 cm floats in mercry with one fifth of the height inside the mercury. Water poured till the surface of the block is just immersed in it. Find the height of the water column to be poured. Specific gravity of mercury =13.6.
View SolutionThe lower end of a capillary tube is immersed in mercury. The level of mercury in the tube is found to be 2 cm below the outer level. If the same tube is immersed in water, up to what height will the water rise in the capillary ?
View SolutionWater and oil are poured into the two limbs of a U-tube containig mercury. The interface of the mercury and the liquids are at the same height in both limbs.
Determine the height of the water columnh1 if that of the oil h2=20cm. The density of the oil is 0.9.
 .
.
View SolutionTwo cyllindrical vessels of equal cross sectional ara A contain water upto heights h1 and h2. The vessels are interconnected so that the levels in them become equal. Calculate the work done by the force of gravity during the process. The density of water is ρ
View Solution
