An open U-tube contains mercury. When 11.2 cm of water is poured into one of the arms of the tube, how high does the mercury rise in the other arm from its initial level ?
0.82 cm
1.35 cm
0.41 cm
2.32 cm
The correct Answer is:C
To solve the problem of how high the mercury rises in the other arm of an open U-tube when 11.2 cm of water is poured into one arm, we can follow these steps:
Step 1: Understand the Pressure Equilibrium
When water is poured into one arm of the U-tube, it exerts pressure on the mercury. The pressure exerted by the water column must equal the pressure exerted by the mercury column in the other arm.
Step 2: Write the Pressure Equations
Let:
- h = height the mercury rises in the other arm (in cm)
- ρw = density of water = 103kg/m3
- ρm = density of mercury = 13.6×103kg/m3
- g = acceleration due to gravity = 9.81m/s2
The pressure due to the water column is given by:
Pwater=ρw⋅g⋅hw
where hw=11.2cm=0.112m.
The pressure due to the mercury column is given by:
Pmercury=ρm⋅g⋅(2h)
because the mercury rises by h in one arm and falls by h in the other arm, making the effective height 2h.
Step 3: Set the Pressures Equal
Since the pressures must balance, we can set them equal to each other:
ρw⋅g⋅hw=ρm⋅g⋅(2h)
Step 4: Cancel g from Both Sides
Since g appears on both sides, we can cancel it out:
ρw⋅hw=ρm⋅(2h)
Step 5: Solve for h
Rearranging the equation to solve for h:
h=ρw⋅hw2⋅ρm
Step 6: Substitute Values
Now, substituting the known values:
h=(103kg/m3)⋅(0.112m)2⋅(13.6×103kg/m3)
Step 7: Calculate h
Calculating the above expression:
h=1122⋅13600=11227200≈0.00412m=0.412cm
Final Answer
The height to which the mercury rises in the other arm is approximately:
h≈0.41cm
---
When water is poured into one arm of the U-tube, it exerts pressure on the mercury. The pressure exerted by the water column must equal the pressure exerted by the mercury column in the other arm.
Let:
- h = height the mercury rises in the other arm (in cm)
- ρw = density of water = 103kg/m3
- ρm = density of mercury = 13.6×103kg/m3
- g = acceleration due to gravity = 9.81m/s2
Pwater=ρw⋅g⋅hw
where hw=11.2cm=0.112m.
Pmercury=ρm⋅g⋅(2h)
because the mercury rises by h in one arm and falls by h in the other arm, making the effective height 2h.
Since the pressures must balance, we can set them equal to each other:
ρw⋅g⋅hw=ρm⋅g⋅(2h)
Since g appears on both sides, we can cancel it out:
ρw⋅hw=ρm⋅(2h)
Rearranging the equation to solve for h:
h=ρw⋅hw2⋅ρm
Now, substituting the known values:
h=(103kg/m3)⋅(0.112m)2⋅(13.6×103kg/m3)
Calculating the above expression:
h=1122⋅13600=11227200≈0.00412m=0.412cm
The height to which the mercury rises in the other arm is approximately:
h≈0.41cm
Topper's Solved these Questions
- FLUID MECHANICSBook:DC PANDEY ENGLISHChapter:FLUID MECHANICSExercise:B) Medical entrance special format question
Explore 19 Videos
- FLUID MECHANICSBook:DC PANDEY ENGLISHChapter:FLUID MECHANICSExercise:Match the columns
Explore 6 Videos
- FLUID MECHANICSBook:DC PANDEY ENGLISHChapter:FLUID MECHANICSExercise:Check point 13.4
Explore 10 Videos
- EXPERIMENTSBook:DC PANDEY ENGLISHChapter:EXPERIMENTSExercise:Subjective
Explore 15 Videos
- GENERAL PHYSICSBook:DC PANDEY ENGLISHChapter:GENERAL PHYSICSExercise:INTEGER_TYPE
Explore 2 Videos
Similar Questions
A simple U tube contains mercury to the same level in both of its arms. If water is poured to a height of 13.6 cm in one arm, how much will be the rise in mercury level in the other arm ?
Given : density of mercury = 13.6×103kg m−3 and density of water = 103kg m−3.
View SolutionA U-shaped tube open to the air at both ends contains some mercury. A quantity of water is carefully poured into the left arm of the U-shaped tube until the vertical height of the water column is 15.0cm.
(a) What is the gauge pressure at the water mercury interface ?
(b) Calculate the vertical distance h from the top of the mercury in the right hand arm of the tube to the top of the water in the left-hand arm.
 .
.
View Solution
Knowledge Check
in previous question, if 15 cm of water and spirit each are further poured into the respective arms of the tube. Difference in the level of mercury in the two arms is (Take, relvative density of mercury = 13.6)
A0.20 cmB0.22 cmC0.27 cmD0.26 cm
Two communicating cylindrical tubes contain mercury. The diameter of one vessel is four times large than the diameter of the outer. A column of water of height 70cm is poured into the narrow vessel. How much wil the mercury level rise in the other vessel and how much will it sink in the narow one? How much will the mercury level rise in the narrow vessel, if a column of water of the same height is pured into the broad vessel?

View SolutionIf 15.0 cm of water and spirit each are further poured into the respective arms of the tube, what is the difference in the levels of mercury in the two arms? (Relative density of mercury = 13.6).
View SolutionThe arms of a U shaped tube are vertical. The arm on right side is closed and other arm is closed by light movable piston. There is mercury in the tube and initially the level of the mercury in the arms is the same. Above the mercury, there is an air column of height h in each arm, and initial pressure is the same as atmospheric pressure in both arms. Now pistion is slowly pushed down by a distance of h/2 (see figure)
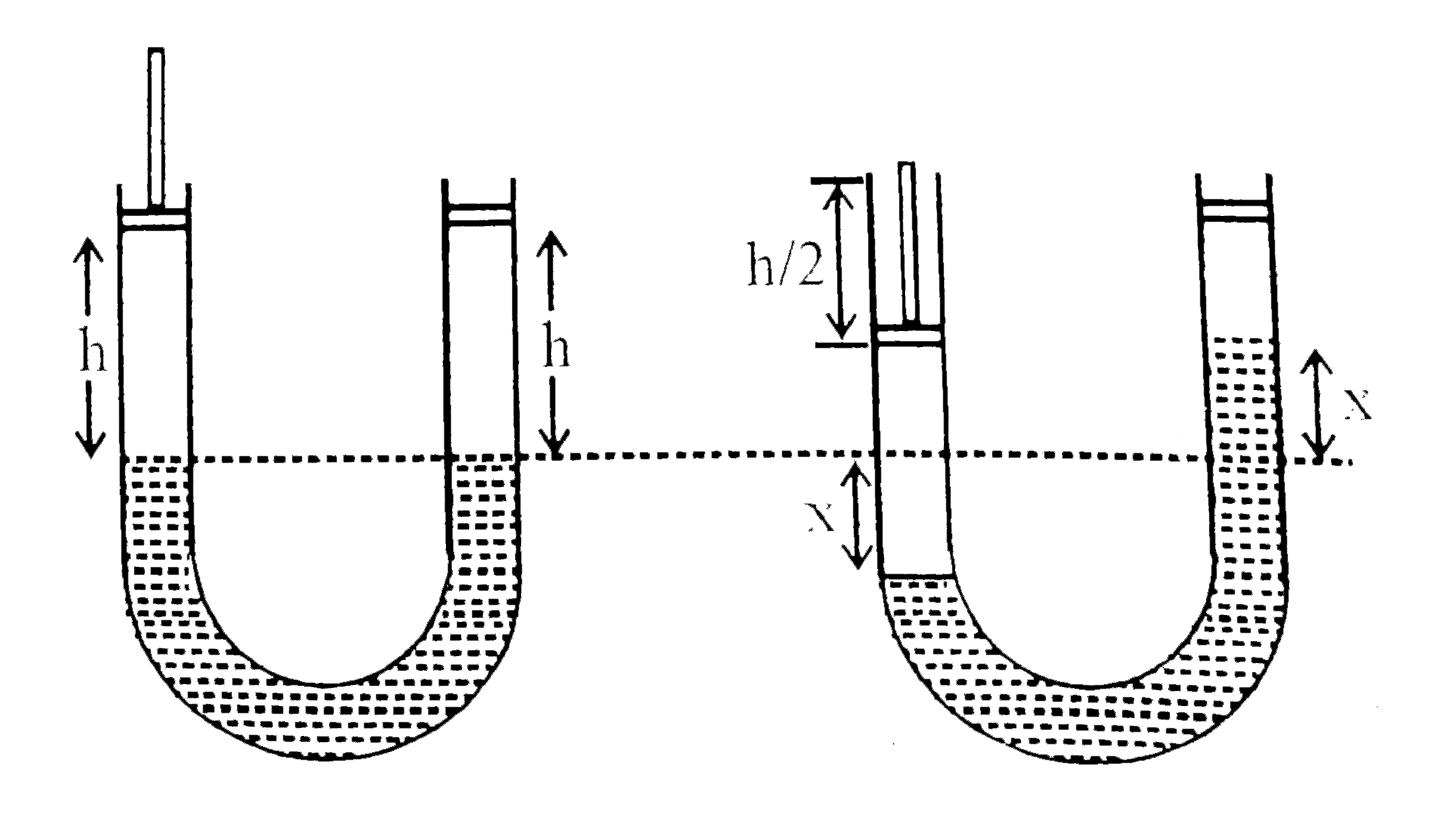
Let x is the displacement of mercury level in one of the stem and P1 is pressure in left column of air after compression, P2 is pressure in right column of air after compression and P0 is atmospheric pressure then
View SolutionA u tube contains water and methylated spirit separated by mercury. The mercury columns in the two arms are at the same levels with 10 cm of water in one arm and 12.5 cm of spirit on the other arm as shown. If 15 cm of water and spirit each are further poured into the respective arms of the tube. Difference in the level of mercury in the two arms is (Take, relative density of mercury = 13.6, relative density of spirit=0.8)
View Solution_S01_015_Q01.png)
A vertical U-tube of uniform cross-section contains mercury in both arms A glycerine (relative density =1.3) column of length 10 cm is introduced into one of the arms. Oil of density 800 gm m−3 is poured into the other arm until the upper surface of the oil and hlycerine are at the same horizontal level, find the length of the column. Density of mercury is 13.6×103kgm−3
View SolutionMercury is poured into a U-tube in which the cross-sectional area of the left-hand limb is three times smaller than that of the right one. The level of the mercury in the narrow limb is a distandce l=30cm from the upper end of the tube. How much will the mercury level rise in the right-hand limb if the left one is filled to the top with water?
View SolutionFigure shows an ideal gas. Its pressure, volume and temperature are P0,V0 and T0 respectively. Thin U-tube contains mercury. It is seen that when 20 cm of extra mercury is added in limb B of U-tube and temperature of gas is doubled, level of A is maintained at its position. Consider surrounding to be vacuum. Find the initial pressure of gas (in cm of Hg.)
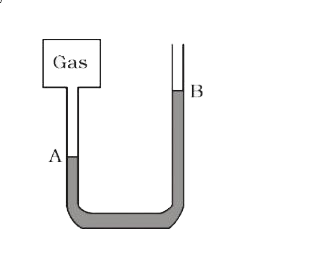
View Solution

