Mercury is poured into a U-tube in which the cross-sectional area of the left-hand limb is three times smaller than that of the right one. The level of the mercury in the narrow limb is a distandce l=30cm from the upper end of the tube. How much will the mercury level rise in the right-hand limb if the left one is filled to the top with water?
The correct Answer is:C
To solve the problem, we will analyze the situation involving a U-tube filled with mercury and water. The left limb has a smaller cross-sectional area compared to the right limb. Let's break down the steps to find out how much the mercury level will rise in the right-hand limb when the left one is filled to the top with water.
1. Understanding the U-tube Setup:
- Let the cross-sectional area of the left limb be A.
- Then the cross-sectional area of the right limb is 3A (since it is three times larger).
- The mercury level in the left limb is at a distance l=30cm from the top of the tube.
2. Setting Up the Pressure Equation:
- When the left limb is filled with water, the pressure at the same height in both limbs must be equal.
- Let hw be the height of the water column in the left limb and hm be the height of the mercury column in the right limb.
- The pressure exerted by the water column is given by:
Pwater=ρwater⋅g⋅hw
- The pressure exerted by the mercury column is:
Pmercury=ρmercury⋅g⋅hm
3. Relating the Heights:
- The height of the water column in the left limb can be expressed as:
hw=30cm+3x
where x is the rise in the mercury level in the right limb.
- The height of the mercury column in the right limb will be:
hm=x
4. Equating the Pressures:
- Since the pressures must balance out:
ρwater⋅g⋅(30+3x)=ρmercury⋅g⋅x
- We can cancel g from both sides:
ρwater⋅(30+3x)=ρmercury⋅x
5. Substituting the Densities:
- The density of water ρwater=1g/cm3 and the density of mercury ρmercury=13.6g/cm3:
1⋅(30+3x)=13.6⋅x
6. Solving for x:
- Rearranging the equation gives:
30+3x=13.6x
30=13.6x−3x
30=10.6x
x=3010.6≈2.83cm
Final Answer:
The mercury level will rise approximately 2.83cm in the right-hand limb.
- Let the cross-sectional area of the left limb be A.
- Then the cross-sectional area of the right limb is 3A (since it is three times larger).
- The mercury level in the left limb is at a distance l=30cm from the top of the tube.
- When the left limb is filled with water, the pressure at the same height in both limbs must be equal.
- Let hw be the height of the water column in the left limb and hm be the height of the mercury column in the right limb.
- The pressure exerted by the water column is given by:
Pwater=ρwater⋅g⋅hw
- The pressure exerted by the mercury column is:
Pmercury=ρmercury⋅g⋅hm
- The height of the water column in the left limb can be expressed as:
hw=30cm+3x
where x is the rise in the mercury level in the right limb.
- The height of the mercury column in the right limb will be:
hm=x
- Since the pressures must balance out:
ρwater⋅g⋅(30+3x)=ρmercury⋅g⋅x
- We can cancel g from both sides:
ρwater⋅(30+3x)=ρmercury⋅x
- The density of water ρwater=1g/cm3 and the density of mercury ρmercury=13.6g/cm3:
1⋅(30+3x)=13.6⋅x
- Rearranging the equation gives:
30+3x=13.6x
30=13.6x−3x
30=10.6x
x=3010.6≈2.83cm
The mercury level will rise approximately 2.83cm in the right-hand limb.
Topper's Solved these Questions
- FLUID MECHANICSBook:DC PANDEY ENGLISHChapter:FLUID MECHANICSExercise:Subjective Question
Explore 2 Videos
- FLUID MECHANICSBook:DC PANDEY ENGLISHChapter:FLUID MECHANICSExercise:Level 2 Single Correct
Explore 36 Videos
- FLUID MECHANICSBook:DC PANDEY ENGLISHChapter:FLUID MECHANICSExercise:Level 1 Single Correct
Explore 49 Videos
- EXPERIMENTSBook:DC PANDEY ENGLISHChapter:EXPERIMENTSExercise:Subjective
Explore 15 Videos
- GENERAL PHYSICSBook:DC PANDEY ENGLISHChapter:GENERAL PHYSICSExercise:INTEGER_TYPE
Explore 2 Videos
Similar Questions
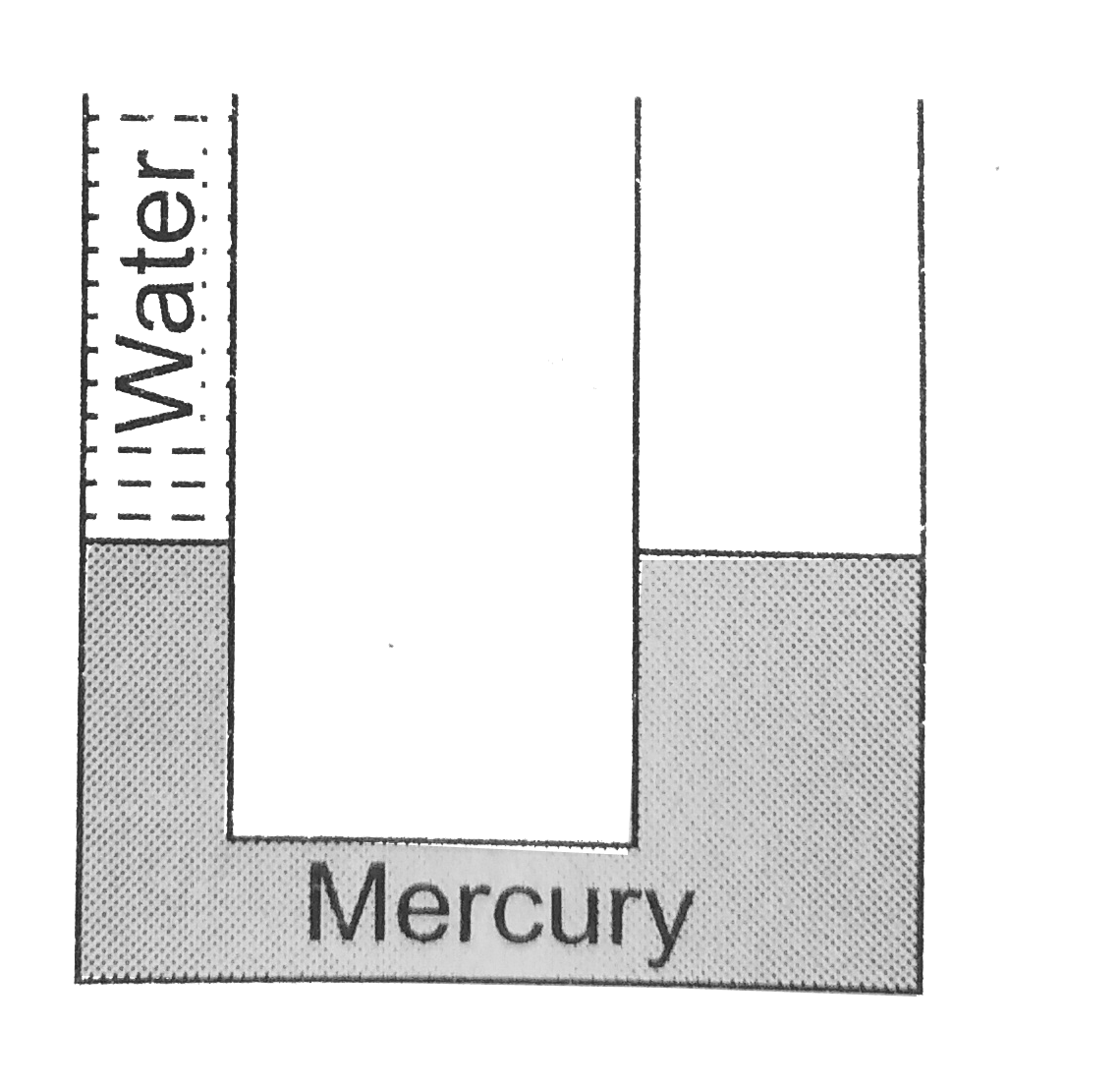
A U -tube in which the cross - sectional area of the limb on the left is one quarter, the limb on the right contains mercury (density13.6g/cm3). The level of mercury in the narrow limb is at a distance of 36 cm from the upper end of the tube. What will be the rise in the level of mercury in the right limb if the left limb is filled to the top with water ?
View SolutionA U-tube in which the cross-sectional area of the limb on the left is one-third of the limb on the right contains mercury (density 13.6g/cm3). The level of mercury in the narrow limb extends to a distance of 30cm from the upper end of the tube. What will be the rise in the level of mercury in the right limb, if the left limb is filled to the top with water (neglect surface tension effects)?

View SolutionA U-shaped tube open to the air at both ends contains some mercury. A quantity of water is carefully poured into the left arm of the U-shaped tube until the vertical height of the water column is 15.0cm.
(a) What is the gauge pressure at the water mercury interface ?
(b) Calculate the vertical distance h from the top of the mercury in the right hand arm of the tube to the top of the water in the left-hand arm.
 .
.
View SolutionAn open U-tube contains mercury. When 11.2 cm of water is poured into one of the arms of the tube, how high does the mercury rise in the other arm from its initial level ?
View SolutionTwo communicating cylindrical tubes contain mercury. The diameter of one vessel is four times large than the diameter of the outer. A column of water of height 70cm is poured into the narrow vessel. How much wil the mercury level rise in the other vessel and how much will it sink in the narow one? How much will the mercury level rise in the narrow vessel, if a column of water of the same height is pured into the broad vessel?

View SolutionA fixed container of height H with large cross-sectional area A is completely filled with water. Two small orifice of cross-sectional area a are made, one at the bottom and the other on the vertical side of the container at a distance H/2 from the top of the container find the time taken by the water level to reach a height of H/2 from the bottom of the container.
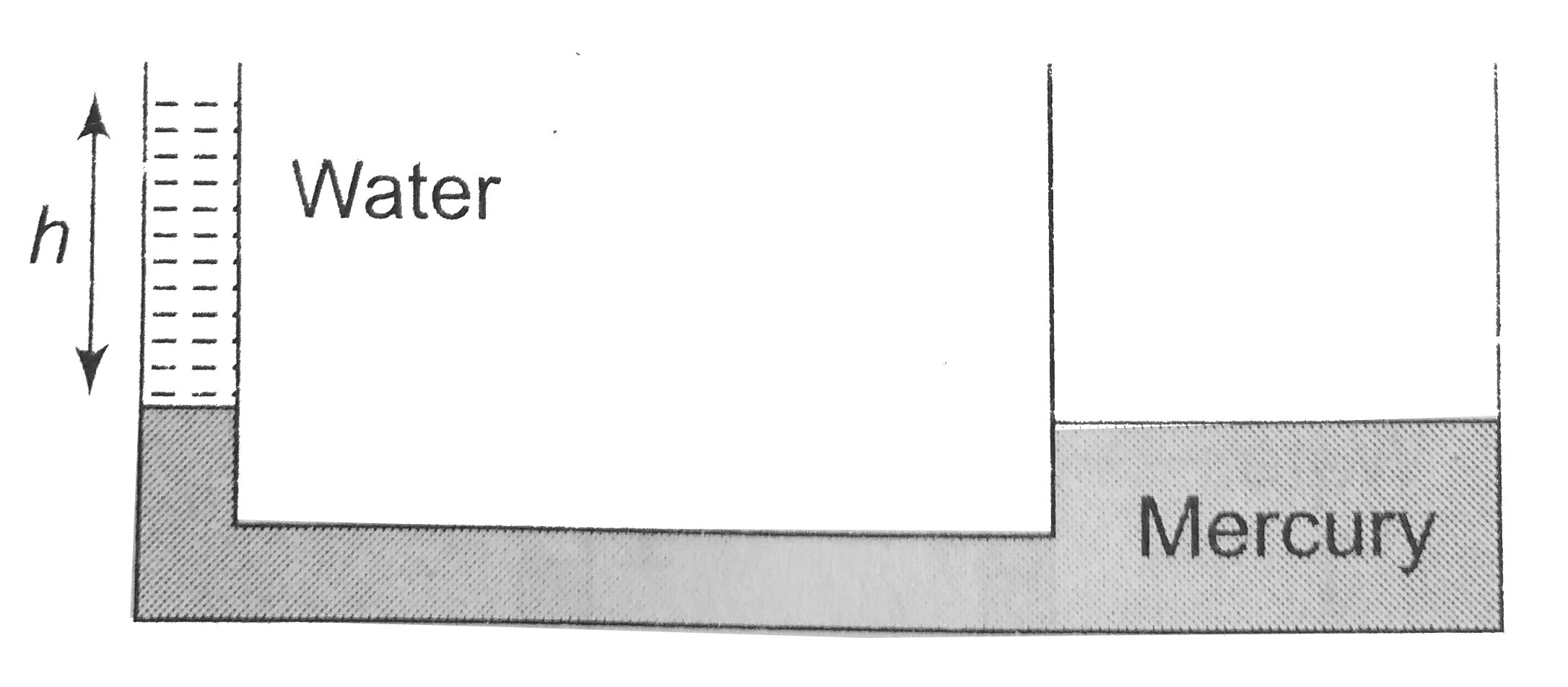
View SolutionTwo communicating vessels contain mercury. The diameter of one vessel in n times larger then the diameter of the other. A column of water of height h is poured into the left vessel. The mercury level will rise in the right hand vessel (s = relative density of mercury and ρ = density of water) by
View SolutionTorricelli was the first do devise an experiment for measuring atmospheric pressure . He took calibrated hard glass tube , 1 m in lengt and of uniform cross section , closed at one end . He filled the whole tube with dry mercury taking care than no air or water droplets remain inside the tube , closed the opposite end of the tube tightly with thumb and inverted it . He put this inverted mercury tube into a mercury through , taking care that the end of the tube remains inside the mercury through , An interesting thing was noticed . Mercury in the tube fell down at first and then stopped at a particular position . The height was 76 cm above the free surface of mercury in the through . When the given tube was inclined or lowered in the mercury trough , the vertical haight of mercury level in the tube was always found constant .
Torricelli explained this by saying that the free surface of mercury in the trough . Hence , the hydrostatic pressure exerted by the trough measures the atmospheric pressure .
If an additional hole is also made at P ' at the top point of the tube , then
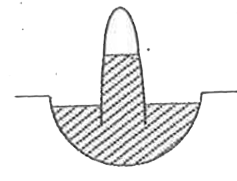
A. mercury will not come out of the tube
B. mercury may come out of the tube after some time .
C. mercury will come out of the tube instantly
D. none of these
View SolutionTorricelli was the first do devise an experiment for measuring atmospheric pressure . He took calibrated hard glass tube , 1 m in lengt and of uniform cross section , closed at one end . He filled the whole tube with dry mercury taking care than no air or water droplets remain inside the tube , closed the opposite end of the tube tightly with thumb and inverted it . He put this inverted mercury tube into a mercury through , taking care that the end of the tube remains inside the mercury through , An interesting thing was noticed . Mercury in the tube fell down at first and then stopped at a particular position . The height was 76 cm above the free surface of mercury in the through . When the given tube was inclined or lowered in the mercury trough , the vertical haight of mercury level in the tube was always found constant .
Torricelli explained this by saying that the free surface of mercury in the trough . Hence , the hydrostatic pressure exerted by the trough measures the atmospheric pressure .

If this expriment uses water instead of mercury , then
A. length of water will be equal to 76 cm
B. length of water will be less than 76 cm
C. length of water will be greater than 76 cm
D. none of the above
View SolutionThe arms of a U shaped tube are vertical. The arm on right side is closed and other arm is closed by light movable piston. There is mercury in the tube and initially the level of the mercury in the arms is the same. Above the mercury, there is an air column of height h in each arm, and initial pressure is the same as atmospheric pressure in both arms. Now pistion is slowly pushed down by a distance of h/2 (see figure)
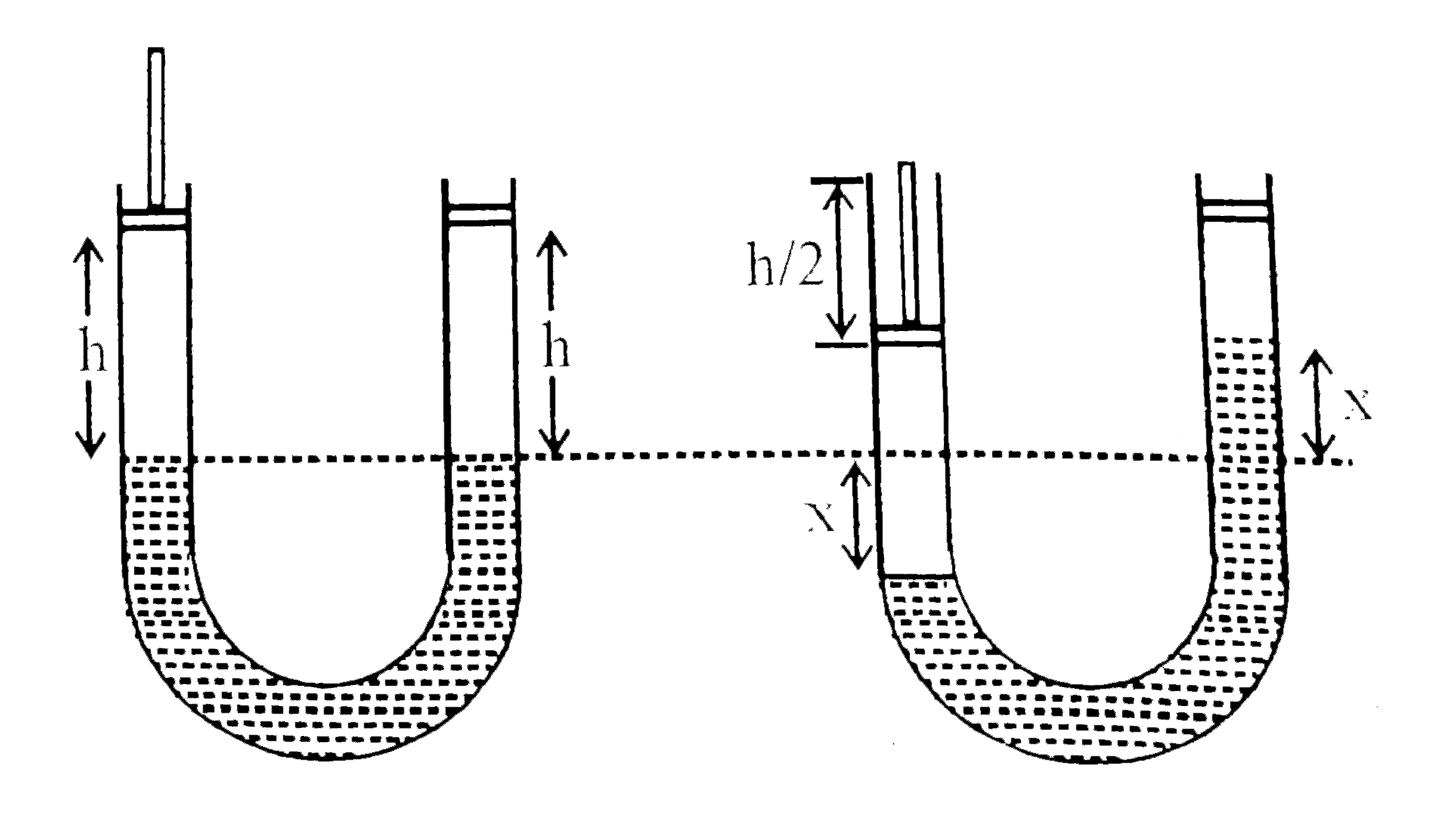
Let x is the displacement of mercury level in one of the stem and P1 is pressure in left column of air after compression, P2 is pressure in right column of air after compression and P0 is atmospheric pressure then
View Solution