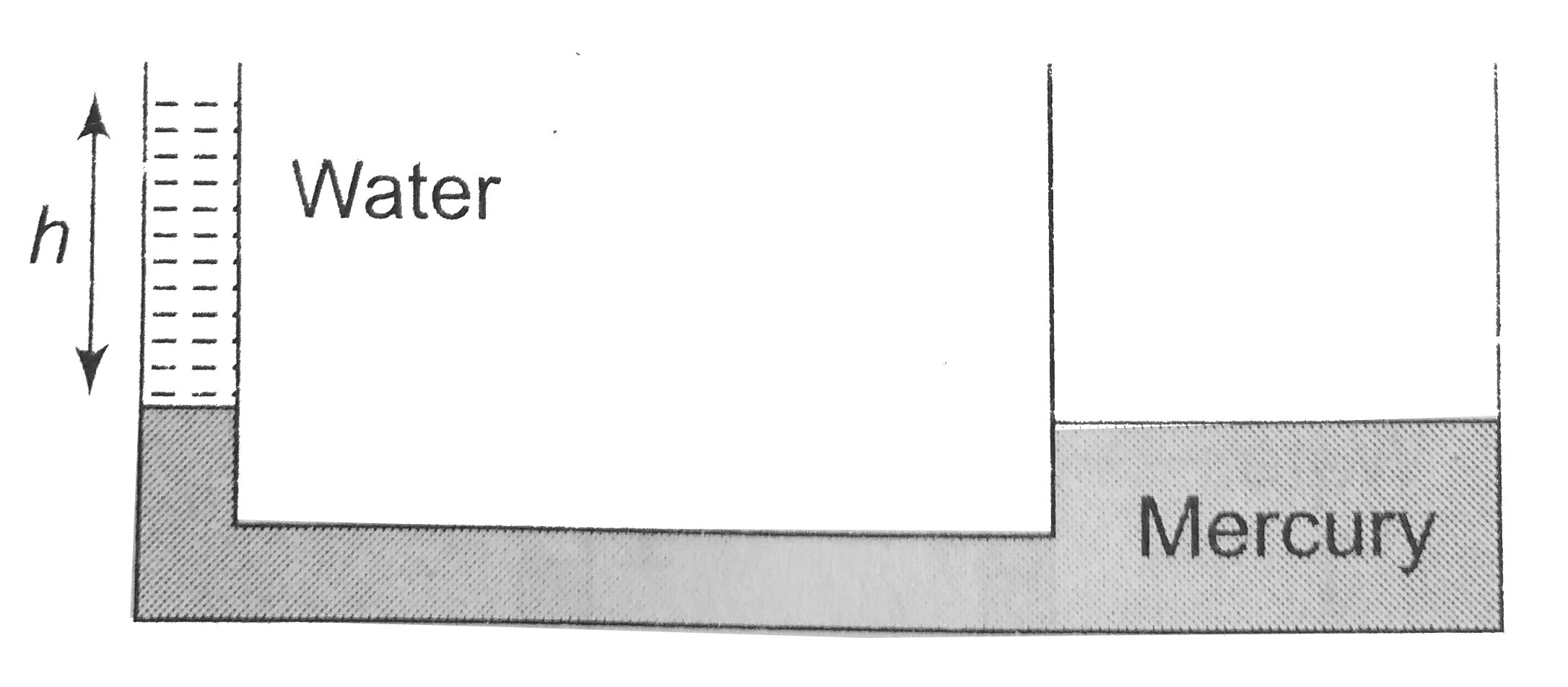
Two communicating cylindrical tubes contain mercury. The diameter of one vessel is four times large than the diameter of the outer. A column of water of height $70 c m$ is poured into the narrow vessel. How much wil the mercury level rise in the other vessel and how much will it sink in the narow one? How much will the mercury level rise in the narrow vessel, if a column of water of the same height is pured into the broad vessel?

Video Solution

Text Solution

Verified by Experts

Let $x =$ rise of $H g$ level in the broad vessel, $y =$ drop of Hg level in the narrow vessel. Then,
$x A_{1} = y A_{2} \Rightarrow 16 x = y$
(because volume displaced will be the same)
Equating pressures at $A$ and $B$ on the same horizontal plane, we get
$70 \times 1 \times g = (x + y) \times 136 \times g \Rightarrow x + y = \frac{70}{13.6}$
Solving the equations, we get $x = 0.3 c m y = 4.8 c m$ . If $70 c m$ water column is pured into the broad vessel, then following the same pattern, we get the equations
$x' = 16 y'$ and $(x' + y') \times 13.6 = 70 \times 1$
$\Rightarrow x' = 4.8 c m$ and $y' = 0.3 c m$

Updated on:21/07/2023

|

Class 11 PHYSICS FLUID MECHANICS

Topper's Solved these Questions

Similar Questions

CENGAGE PHYSICS ENGLISH-FLUID MECHANICS-INTEGER_TYPE

Home
Ask Doubt
Profile