A small bar A resting on a smooth horizontal plane is attached by threads to a point P and by means of weightless pulley, to a weight B possessing the same mass as the bar itself. The bar is also attached to a point O by means of a light non-deformed spring of length l0=50cm and stiffness k=5mg/l0, where m is the mass of the bar. The thread PA having been burned, the bar starts moving to the right. Find its velocity at the moment when it is breaking off the plane.

Let θ be the angle between spring and vertical at the instant when block A breaks off the plane (N=0).
⇒cosθ=l0l0+x (i)
N+kxcosθ=mg
⇒kxcosθ=mg (as N=0) (ii)
Let d is the distance covered by A and B till this instant and V is the speed acquired by A and B.
(same because they are connected)
From (i) and (ii), using k=5mgl0
⇒5mgl0×l0l0+x=mg
⇒x=l4l0⇒d=√(l0+x)2−l20=3l04
Using energy conservation:
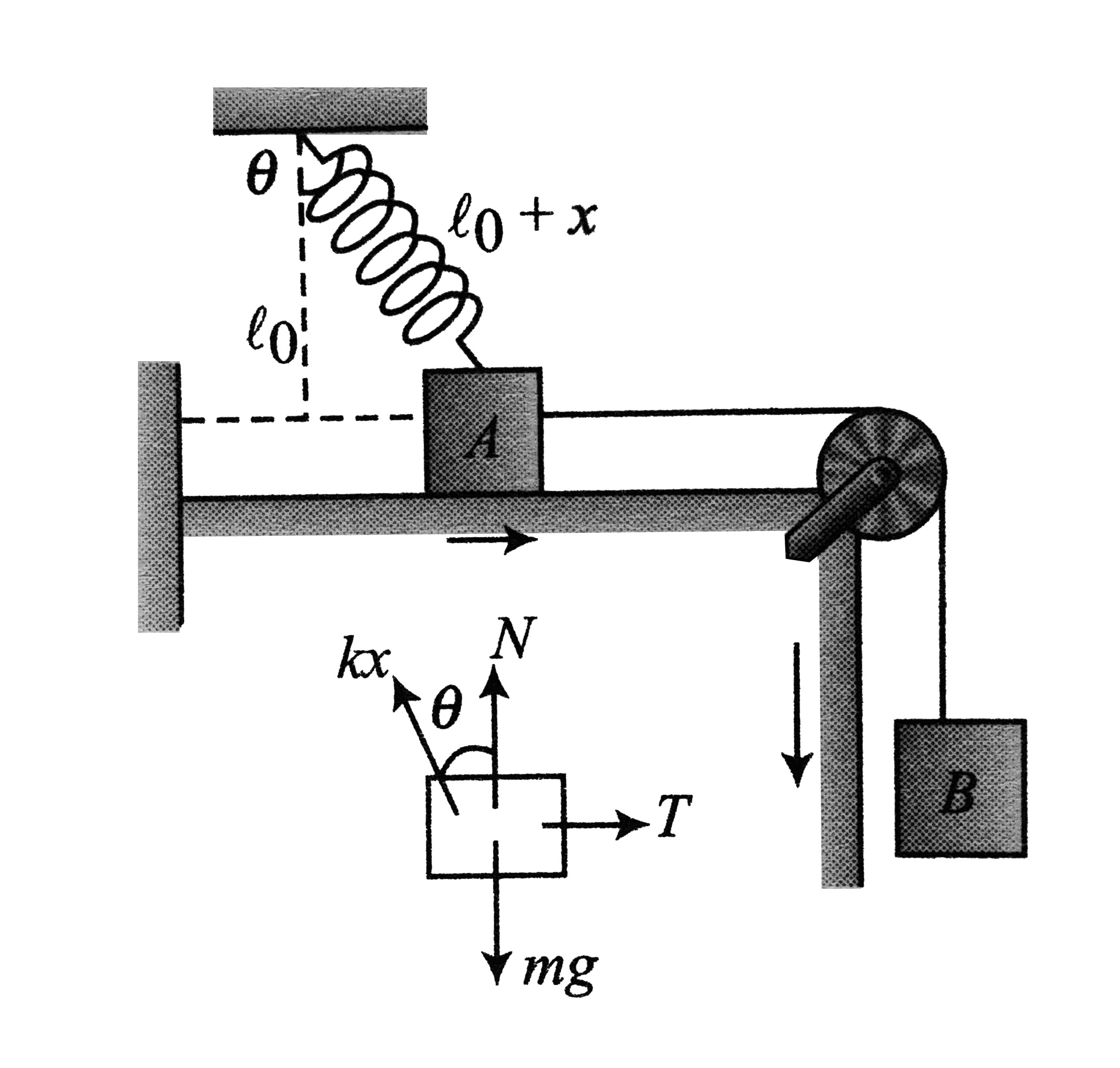
mgd=2(12mv2)+12kx2
⇒mg(3l0)4=mv2+125mgl0l2016
⇒v2=3gl04−532gl0⇒v=√19gl032
Topper's Solved these Questions
- WORK, POWER & ENERGYBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - WORK, POWER & ENERGYEXERCISE - Exercise 8.1
25 Videos
- WORK, POWER & ENERGYBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - WORK, POWER & ENERGYEXERCISE - Exercise 8.2
25 Videos
- WORK, POWER & ENERGYBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - WORK, POWER & ENERGYEXERCISE - Archives (integer)
4 Videos
- VECTORSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - VECTORSEXERCISE - Exercise Multiple Correct
5 Videos
Similar Questions
Choose the correct option:
Two bars of masses m1 and m2 connected by a weightless spring of stiffness k, rest on a smooth horizontal plane. Bar 2 is shifted by a small distance x0 to the left and released. The velocity of the centre of mass of the system when bar 1 breaks off the wall is
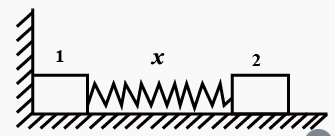
View SolutionTwo bars of masses m1 and m2 connected by a weightless spring of stiffness k, rest on a smooth horizontal plane. Bar 2 is shifted by a small distance x0 to the left and released. The veloicyt of the centre of mass of the system when bar 1 breaks off the wall is

View Solution
Knowledge Check
Give the symbolic meaning of 'bar' in the line, 'no moaning of the bar'.
AHarbour soundsBsand bar in the seaCsounds within the ship yardDrelations and things that bind the soul to the earth
What is the magnitude of the equatorial and axial fields due to a bar manget of length 5⋅0cm at a distance of 50cm from its mid-point? The magnetic moment of the bar magnet is 0⋅40Am2.
View SolutionWhat is the magnitude of the equatorial and axial fields due to a bar manget of length 5⋅0cm at a distance of 50cm from its mid-point? The magnetic moment of the bar magnet is 0⋅40Am2.
View SolutionA particle of mass m attached to a string of length l is descending circular motion on a smooth plane inclined at an angle α with the horizontal. For the particle to reach the highest point its velocity at the lowest point should exceed.
View SolutionA spherical bob of mass m and radius R is attached to a fixed point by means of a massless rigid rod whose length from the point of support up to the centre of bob is l. Find the period of small oscillation.
View SolutionA horizontal plane supports a plank with a bar of mass m placed on it and attached by a light elastic non-deformed cord of length l0, to a point O. The coefficient of friciton between the bar and the plank is equal to m. The plank is slowly shifted to the right until the bar starts sliding over it. It occurs at the moment when the cord derivates from the vertical by an angle θ.
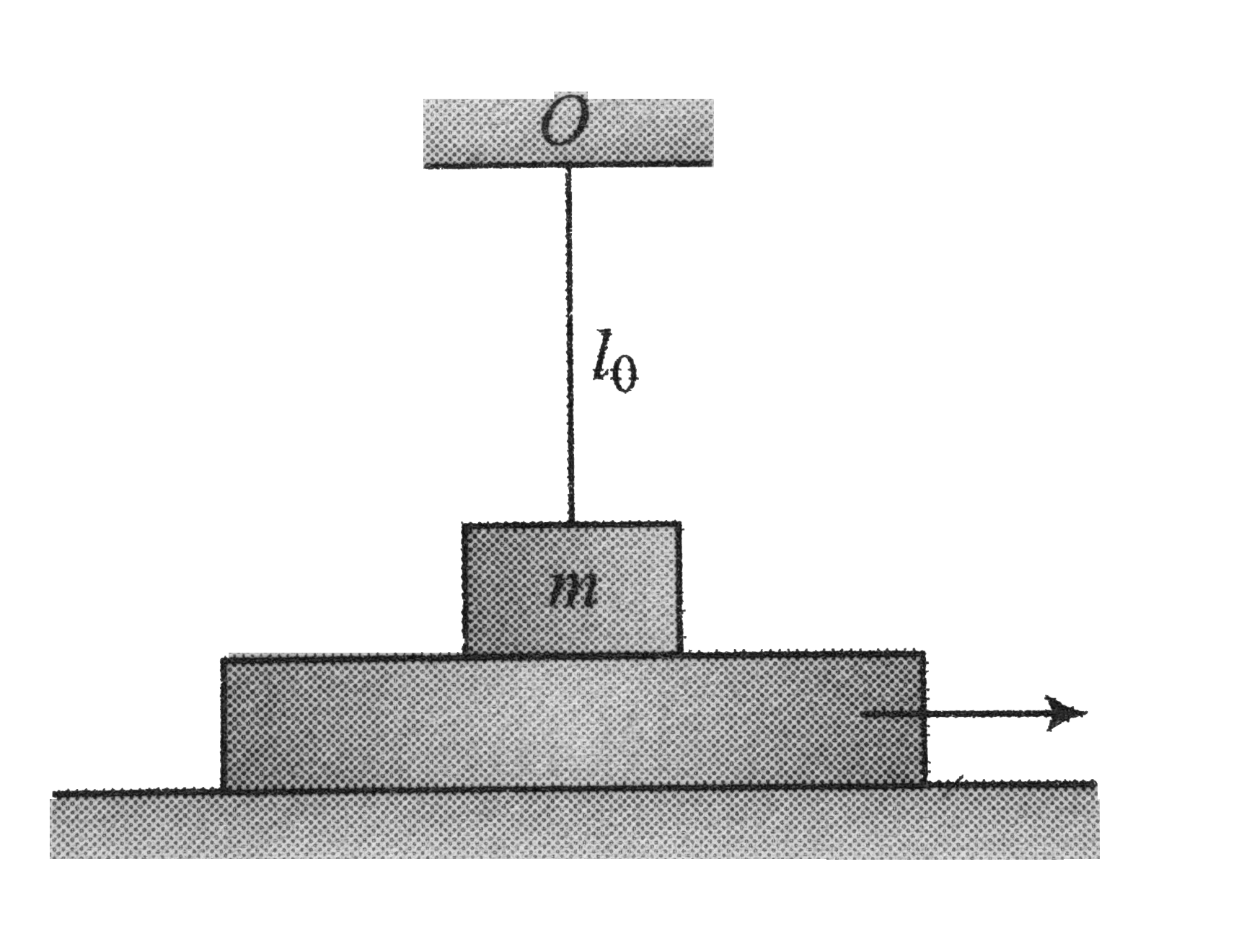
Find the work that has been performed by the moment by the frictional force acting on the bar in the reference frame fixed to the plane.
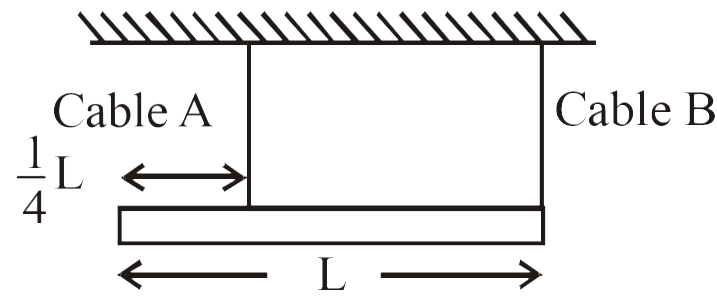
View SolutionA uniform bar of mass M and length L is horizontally suspended from the ceiling by two vertical light cables as shown. Cable A is connected 14th distance from the left end of the bar. Cable B is attached at the far right end of the bar. What is the tension in cable A?
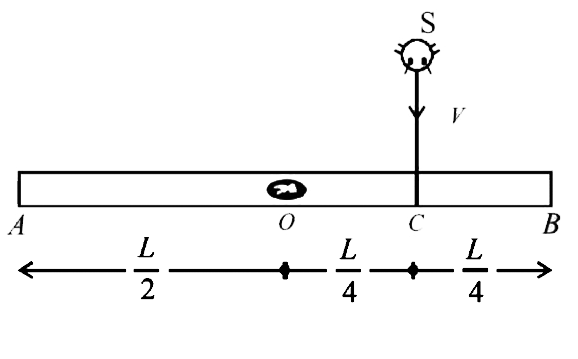
View SolutionA thin uniform bar lies on a frictionless horizonta surface and is free to move in any way on th surface. Its mass is 0.16 kg and length √3meters. Two particless, each of mass 0.08 kg, are moving on the same surface and towards the bar in a direction perpendicular to the bar, one with a velocity of 10 m/s, and other with 6m/s as shown in fig. The first particle strikes the bar at point A and the other at point B. Points A and B are at a distane of 0.5m from the centre of the bar. The particles strike the bar at the same instant of time and stick to the bar on collision. Calculate the loss of the kinetic energy of the system in the above collision process.
View Solution
