Two identical blocks A and B, each of mass m=2kg are connected to the ends of an ideal spring having force constant K=1000Nm−1. System of these blocks and spring is placed on a rough floor. Coefficient of friction between blocks and floor is m=0.5. Block B is passed towards left so that spring gets compressed.
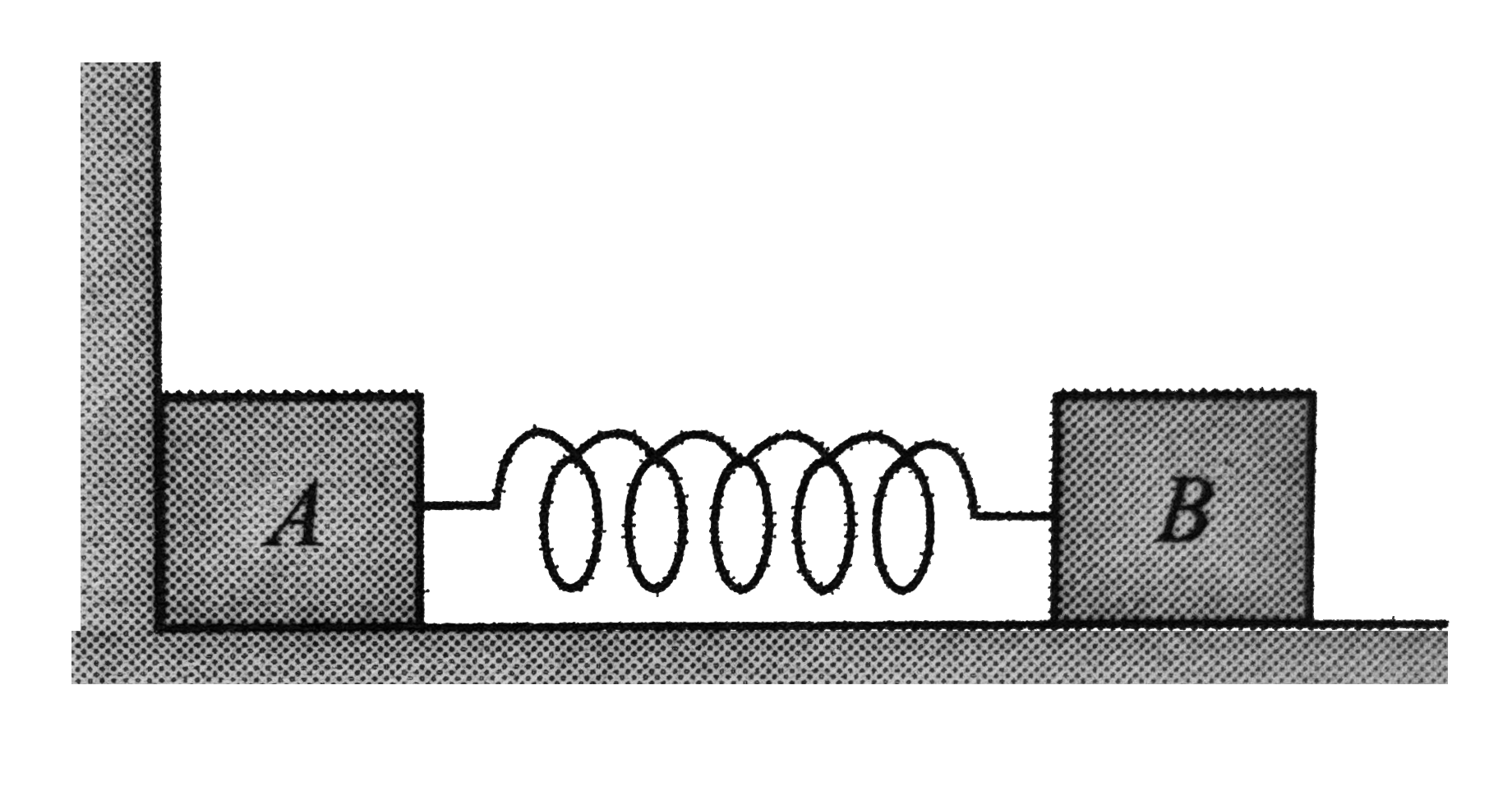
Calculate initial minimum compression x0 of spring such that block A leaves contact with the wall when system is released.
Since, spring is initially compressed, therefore, on releasing the system, block B experiences a resultant force ( to the right) and system, block B experiences a resultant force (to the right) and starts moving to the right.
Block A leaves contact with the wall when rightward force on it applied by spring becomes just equal to the force of friction between this block and floor. Let at that instant, elongation of spring (from its natural length) be x′, then tension in spring is T=Kx′=1000x′ newton. Considering free body diagram of A at that instant.
V1=mg=20N
1000.x′=μ.V1=0.5×20
x′=0.01m
Since spring was initially compressed by x0 and it has an elongation of x′, therefore, displacement of block B (upto this instant)=x0=x′.
According to the law of conservation of energy,
Decrease in energy stored in the spring = Work done by block B against friction
[12Kx20−12K(x′)2]=μmg(x0+x′)
Substituting x′=0.01m, K=1000Nm−1, μ=0.5, n=2kg and x0=0.03cm.
If initial compression of spring is x=2x0=6cm, initial energy stored in spring is
U0=12K(2x0)2=1.80J
When block A loses contanct with the wall, at that instant, elongation of spring (from natural length) is x′=1cm.
At that instant energy stored in the spring is ,
U=12K(x′)2=0.05J
Decrease in energy stored in the spring is,
(U0−U)=1.75J
This energy is used in two ways.
To over come frictional loss during motion of block. But displacement of block B is (2x0+x′)=7cm. Hence, energy lost against friction is
μmg=(2x0+x′)=0.7J
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - WORK, POWER & ENERGYEXERCISE - Exercise 8.125videos
WORK, POWER & ENERGY
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - WORK, POWER & ENERGYEXERCISE - Exercise 8.225videos
WORK, POWER & ENERGY
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - WORK, POWER & ENERGYEXERCISE - Archives (integer)4videos
WORK, POWER & ENERGY
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - VECTORSEXERCISE - Exercise Multiple Correct5videos
VECTORS
Similar Questions
A block of mass 50 kg is projected horizontal on a rough horizontal floor. The coefficient of friction between the block and the floor is 0.1. The block strikes a light spring of stiffness k=100N/m with a velocity 2m/s, the maximum compression of the spring is
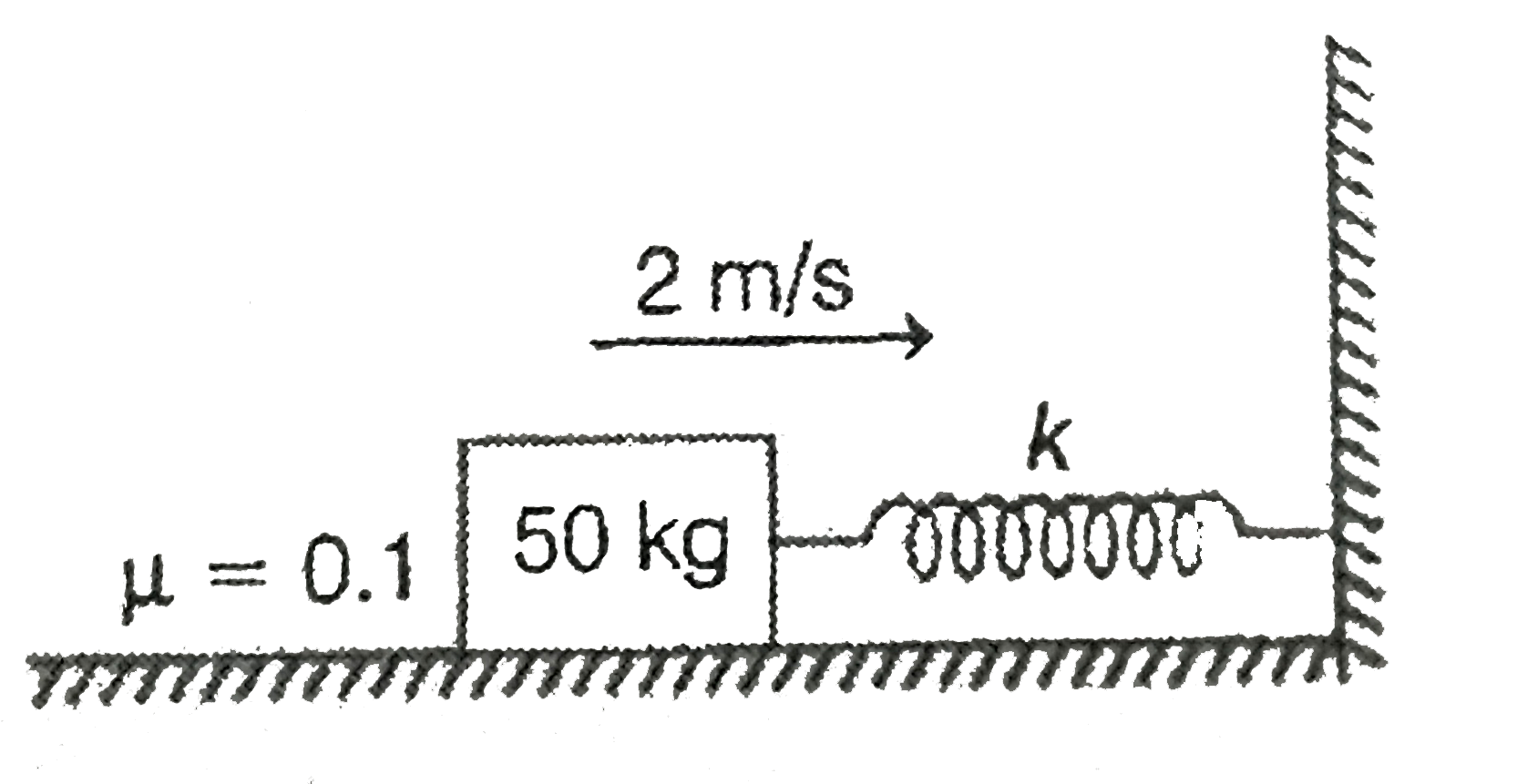 View Solution
View SolutionA block of mass m is attached to one end of a mass less spring of spring constant k. the other end of spring is fixed to a wall the block can move on a horizontal rough surface. The coefficient of friction between the block and the surface is μ then the compession of the spring for which maximum extension of the spring becomes half of maximum compression is .
View SolutionA block of mass m attached with a an ideal spring of force constant k is placed on a rough inclined plane having inclination θ with the horizontal and coefficient of friction μ=1/2tanθ, Initially the block is held stationary with the spring in its relaxed state, find the maximum extension in the spring if the block is released.
 View Solution
View SolutionA block A of mass m=5kg is attached with a spring having force constant K=2000Nm−1. The other end of the spring is fixed to a rough plane, inclined at 37∘ with horizontal and having coefficient of friction m=0.25. Block A is gently placed on the plane such that the spring has no tension. Then block A is released slowly. Calculate elongation of the spring when equilibrium is achieved. Now an inextensible thread is connected with block A and passes below pulley C and over pulley D, as shown in figure. Other end of the thread is connected with another block B of mass 3kg. Block B is resting over a table and thread is loose. If the table collapse suddenly and B falls freely through 80/9cm, the thread becomes taut, calculate combined speed of blocks at that instant, and maximum elongation of spring in the process of motion. (g=10ms−2).
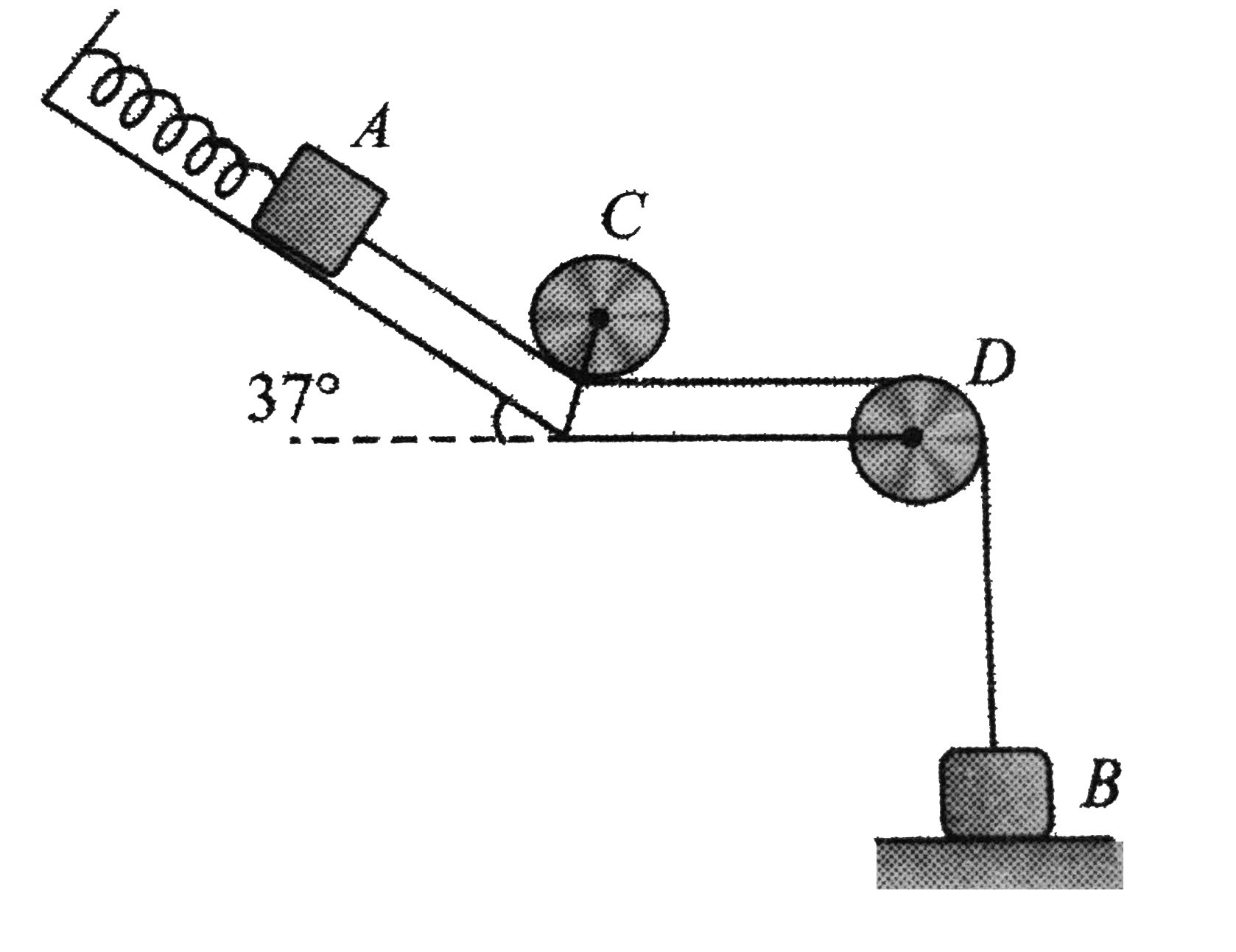 View Solution
View SolutionTwo blocks each having mass m is attached to each other with a spring having force constant k. The system is placed on a rough horizontal surface having coefficient of friction μ. The maximum initial compression, that can be given to the spring so that when released the blocks do not move is
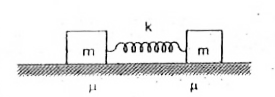 View Solution
View SolutionTwo blocks of masses m1 and m2 are connected by an ideal sprit, of force constant k. The blocks are placed on smooth horizontal surface. A horizontal force F acts on the block m1. Initially spring is relaxed, both the blocks are at rest.

What is acceleration of centre of mass of system at the instant of maximum elongation of springView SolutionA small block of mass 2 kg is placed on a bigger block of mass 4 kg which is attached to horizontal spring of spring constant K=500N/m as shown in figure, coefficient of friction between block is 0.2 .Maximum amplitude of system so that there is no relative slipping between blocks.
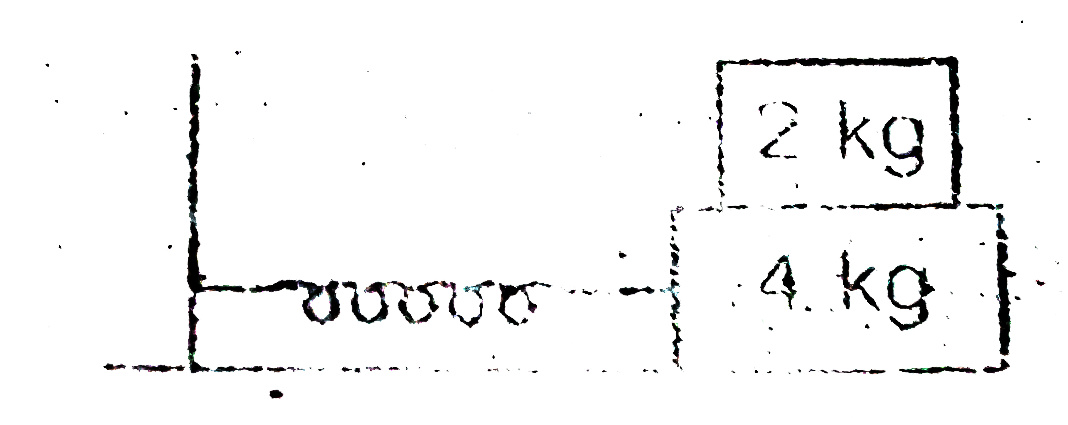 View Solution
View SolutionA block of mass m is connected to another .block of mass M by a massless spring of spring constant k. A constant force f starts action as shown in figure, then:
 View Solution
View SolutionTwo identical blocks A and B of mass m each are connected to each other by spring of spring constant k. Block B is initially shifted to a small distance x0 to the left and then released. Choose the correct statements for this problem, after the spring attains it's natural length.
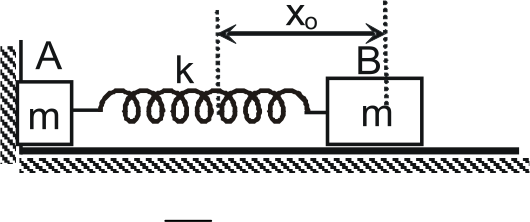 View Solution
View SolutionA block of mass m=2kg is connected to a a spring of force constant k=50N/m. Initially the block is at rest and tlhe spring has natural length. A constant force F=60N is applied horizontally towards, the maximum speed of the block (in m/s) will be (negelect friction).
 View Solution
View Solution
