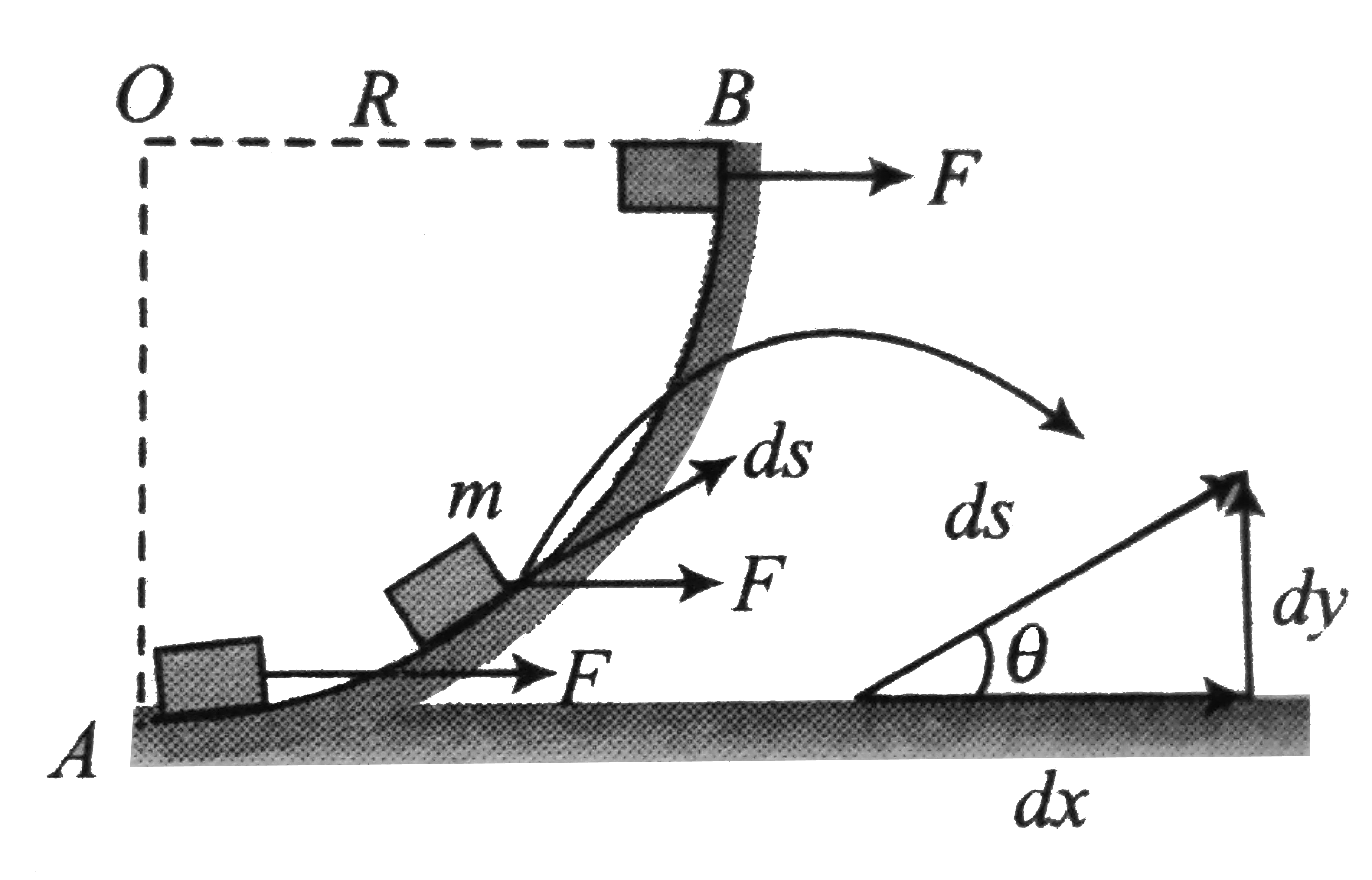
Figure. A smooth circular path of radius R on the horizontal plane which is quarter of a circle A block of mass m is taken from position A to B under the action of a constant force F. Calculate the work done by force F.
a. If it is always directed horizontally
b. If the block is pulled by a force F which is always tangential to the surface
c. Block is pulled with a constant force F which is always directed towards the point B
a.
or
As the block moves from A to B, the displacement of the block in the direction of force is equal to radius R.
Therefore, the work by the constant force is .
b. If the block is pulled by a force F which is always tangential to the surface, in this case, force and displacement are always parallel to each other. The displacement of the block in the direction of force is .
Thus, the work done by the force is
c. Block is pulled with a constant force F which is always directed towards the point B. In this case, angle between force vector and displacement vector is varying.
In figure the angle between and is . Block is at angle from vertical The magnitude of is R. The relation between and is
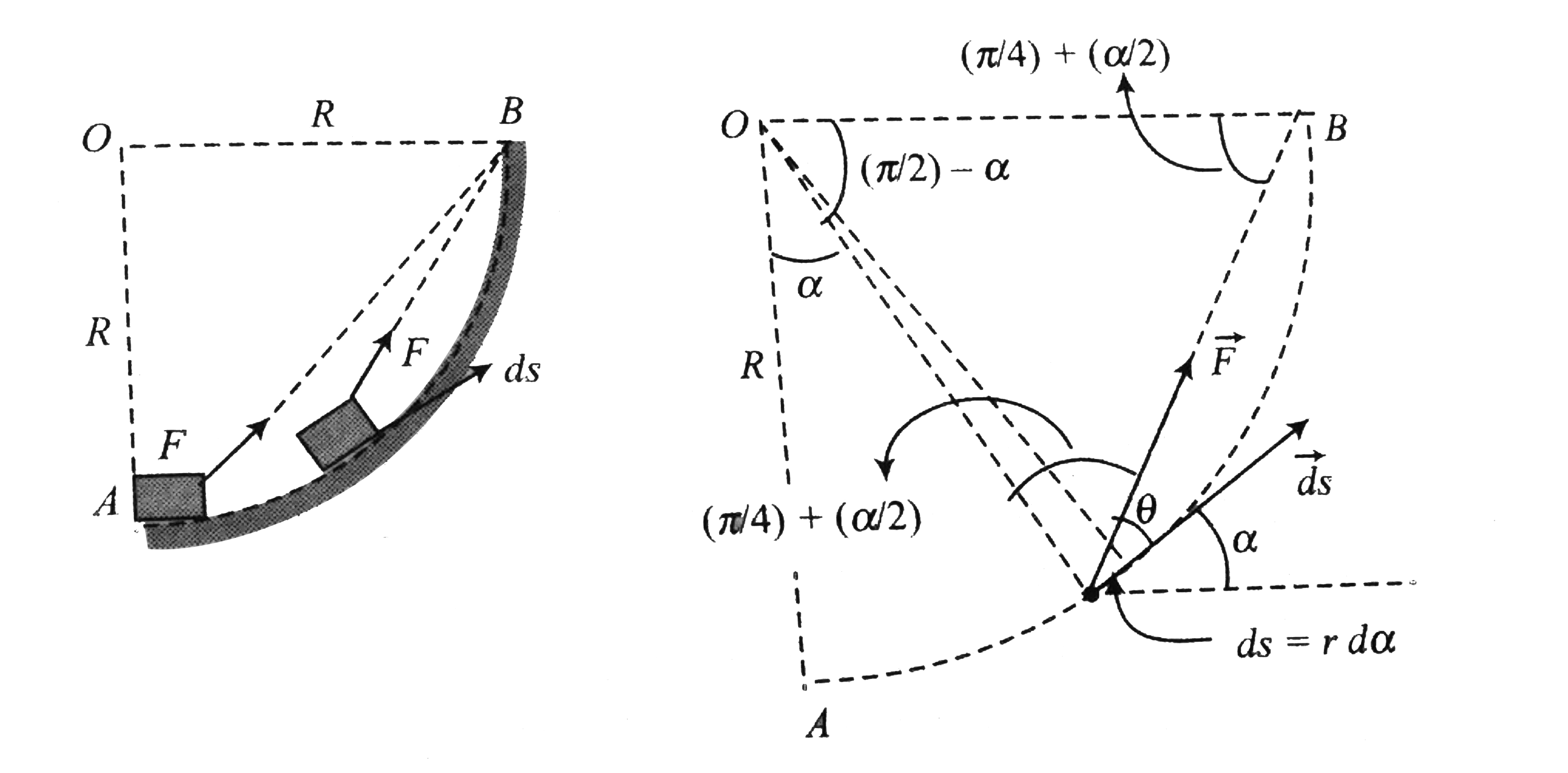
Thus,
or
or
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - WORK, POWER & ENERGYEXERCISE - Exercise 8.125videos
WORK, POWER & ENERGY
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - WORK, POWER & ENERGYEXERCISE - Exercise 8.225videos
WORK, POWER & ENERGY
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - WORK, POWER & ENERGYEXERCISE - Archives (integer)4videos
WORK, POWER & ENERGY
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - VECTORSEXERCISE - Exercise Multiple Correct5videos
VECTORS
Similar Questions
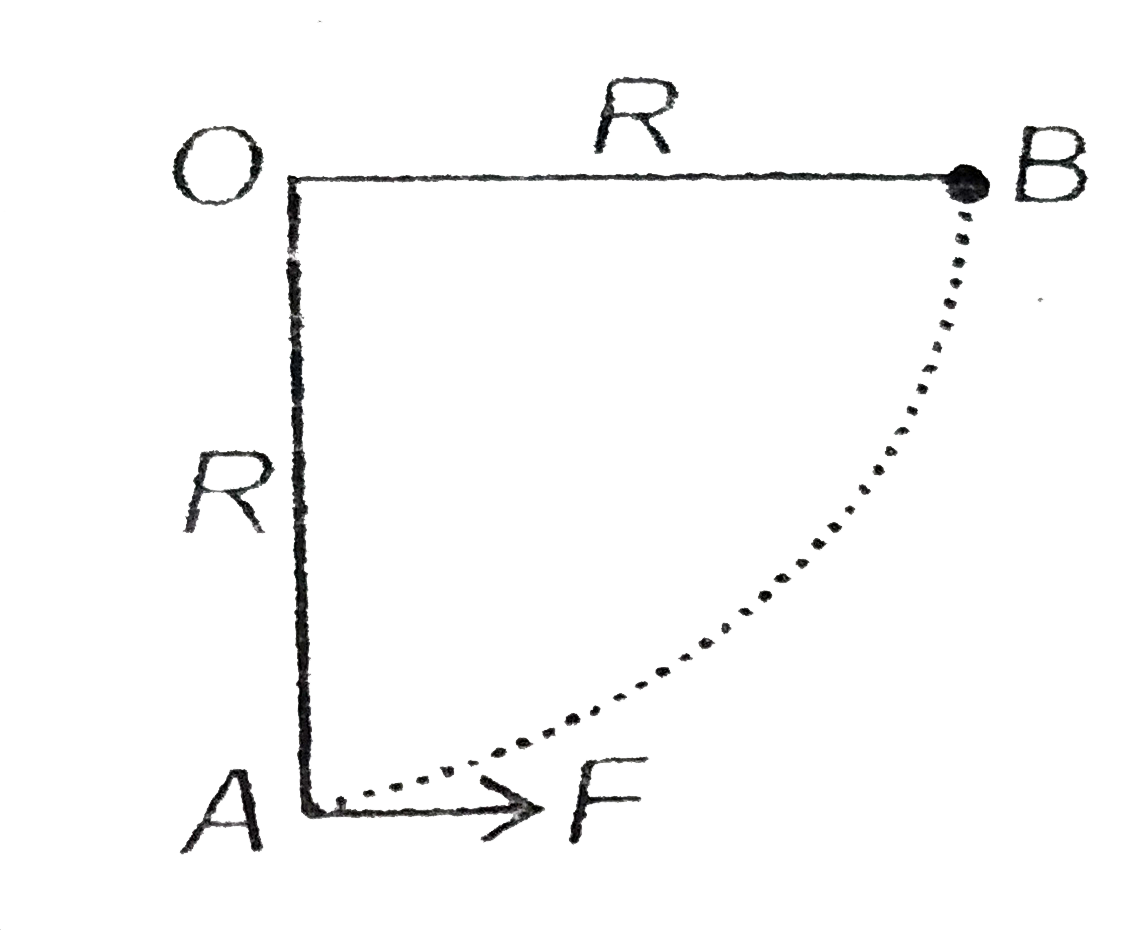
A block of mass m is taken from A to B under the action of a constant force F. Work done by this force is
 View Solution
View SolutionA block of mass m is at rest under the action of force F against a wall as shown in figure. Which of the following statement is incorrect?
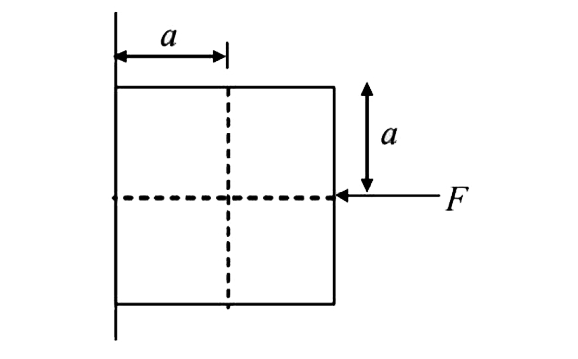 View Solution
View SolutionA horizontal force F pushes wedge of mass M on a smooth horizontal surface. A block of mass m is stationary to the wedge, then:
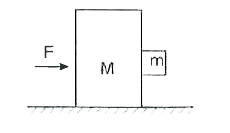 View Solution
View SolutionA particle of mass M moves with constant speed along a circular path of radius r under the action of a force F. Its speed is
View SolutionA block of mass 2 kg is pulled along circular arc from position X to Y as shown in figure. The work done by the horizontal force is pulling the block from X to Y is
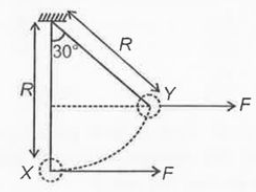 View Solution
View SolutionA block of mass m, lying on a smooth horizontal surface, is attached to a spring (of negligible mass) of spring constant k. The other end of the spring is fixed, as shown in the figure. The block is initally at rest in its equilibrium position. If now the block is pulled withe a constant force F, the maximum speed of the block is :
 View Solution
View SolutionA force F is applied on a block of mass M. The block is displaced through a distance d in the direction of the force. What is the work done by the force on the block? Does the internal energy change because of this work?
View SolutionA bob of mass m is pulled along a circular arc by means of a constant horizontal force P as shown. Work done in lifting the bob from A to B is
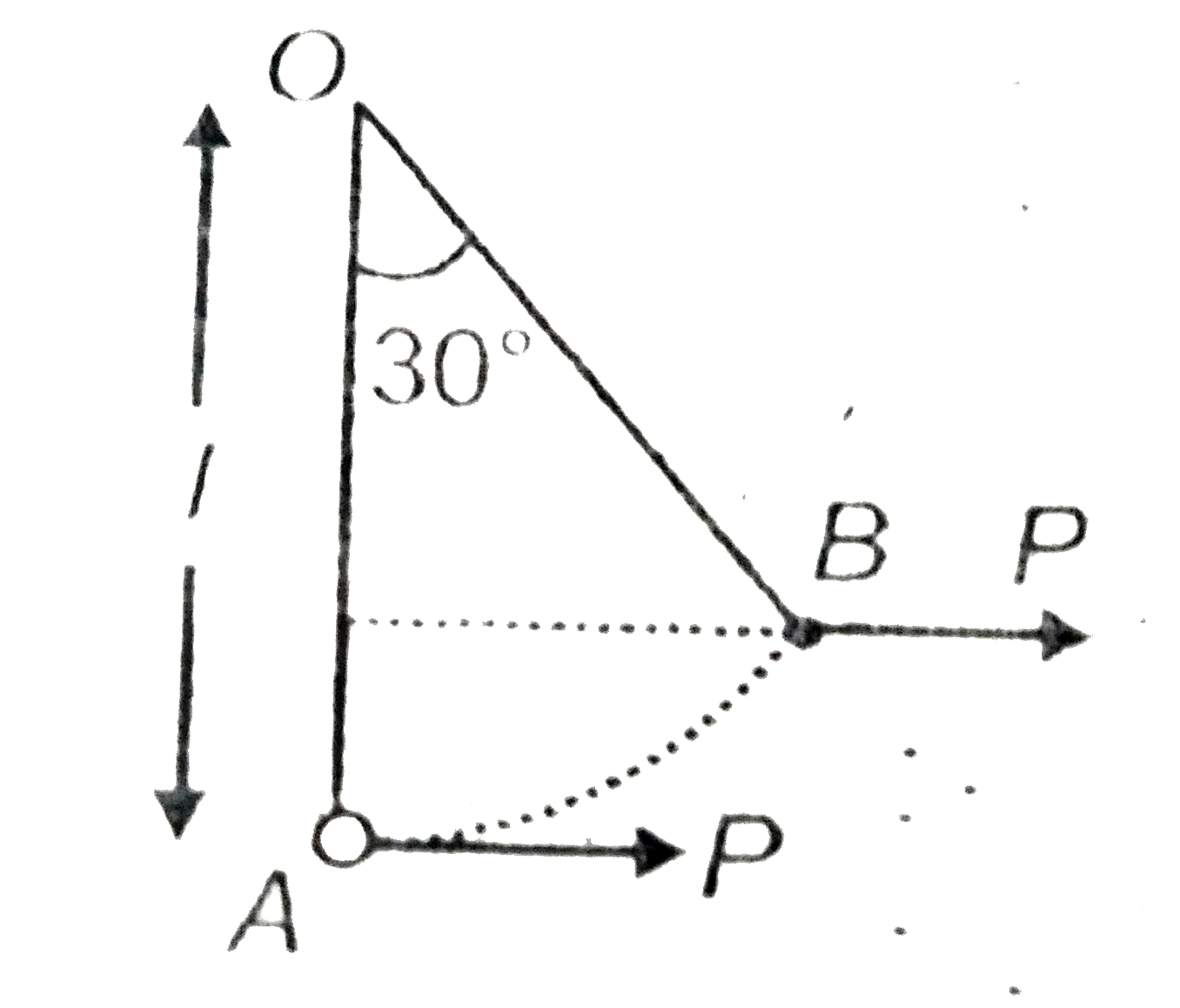 View Solution
View SolutionA block of mass m is placed in contact with one end of a smooth tube of mass M. A horizontal force F acts on the tube in each case (i) and (ii). Then,
 View Solution
View SolutionAn object of mass M and radius R is performing pure rolling motion on a smooth horizontal surface under the action of a constant force F as shown in Fig. The object may be
 View Solution
View Solution
