A spherical balll of mass m is the highest point in the space between two fixed , concentic sphere A and B the smaller the two sphere A has a radius R and the space between the two spheres has a width d . The bell has a disneter very dightly less then d . All surface are frictionless . The bell is a given a gentle push (owards the right in the figure ) The upward vertical is denoted by θ (shown ijn the figure)

(a)Express the total normal reaction force exerted by the sphore on the as a finction of angle θ
(b) Let N_(A)andNBdenote in the magnitubes of the normal reaction force on the bell evered by the sphare A and B repectively Skech the variation of NAandN_(B)asfunctionsofcos theta ∈theran≥0 le theta le pi bydraw∈gtwoseparategraph∈youranswerb∞ktak∈gcos theta an the horizental axas.
The ball is moving in a circulaar motion. The necessary centripetal force is provided by (mgcosθ−N). Therefore,
mgcosθ−NA=mv2[R+(d/2)]2 (i)
According to energy conservation,
12mv2=mg(R+d2)(1−cosθ) (ii)
From Eqs (i) and (ii), we get
NA=mg(3cosθ−2) (iii)
The above equation shows that as θ increases, NA decreases. At a particular value of θ, NA will become zero and the ball will lose contact with sphere A. This condition can be found by putting
NA=0 in Eq. (iii).
0=mg(3cosθ−2)
∴θ=cos−1(23)
The graph between NA and cosθ is shown in figure.
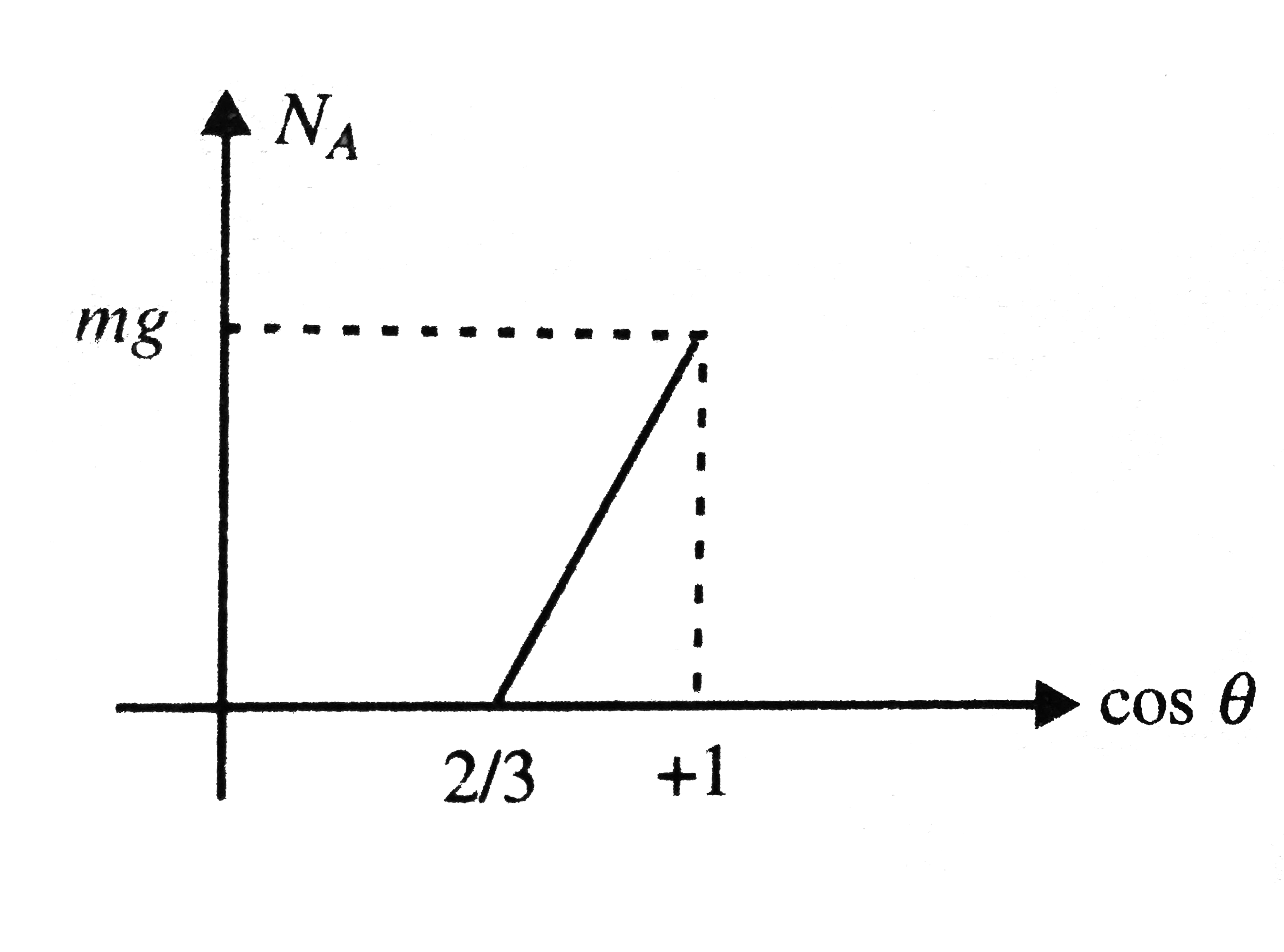
From Eq. (iii), when θ=0, NA=mg.
When θ=cos−1(23), NA=0.
The graph is a straight line as shown in figure.
When θ>cos−1(23)
NB+mgcosθ=mv2(R+d2) (iv)
Using energy conservation, we get
12mv2=mg[(R+d2)−(R+d2)cosθ]
mv2(R+d2)=2mg[1−cosθ]
From Eqs. (iv) and (v), we get
NB+mgcosθ=2mg−2mgcosθ
⇒NB=mg(2−3cosθ)
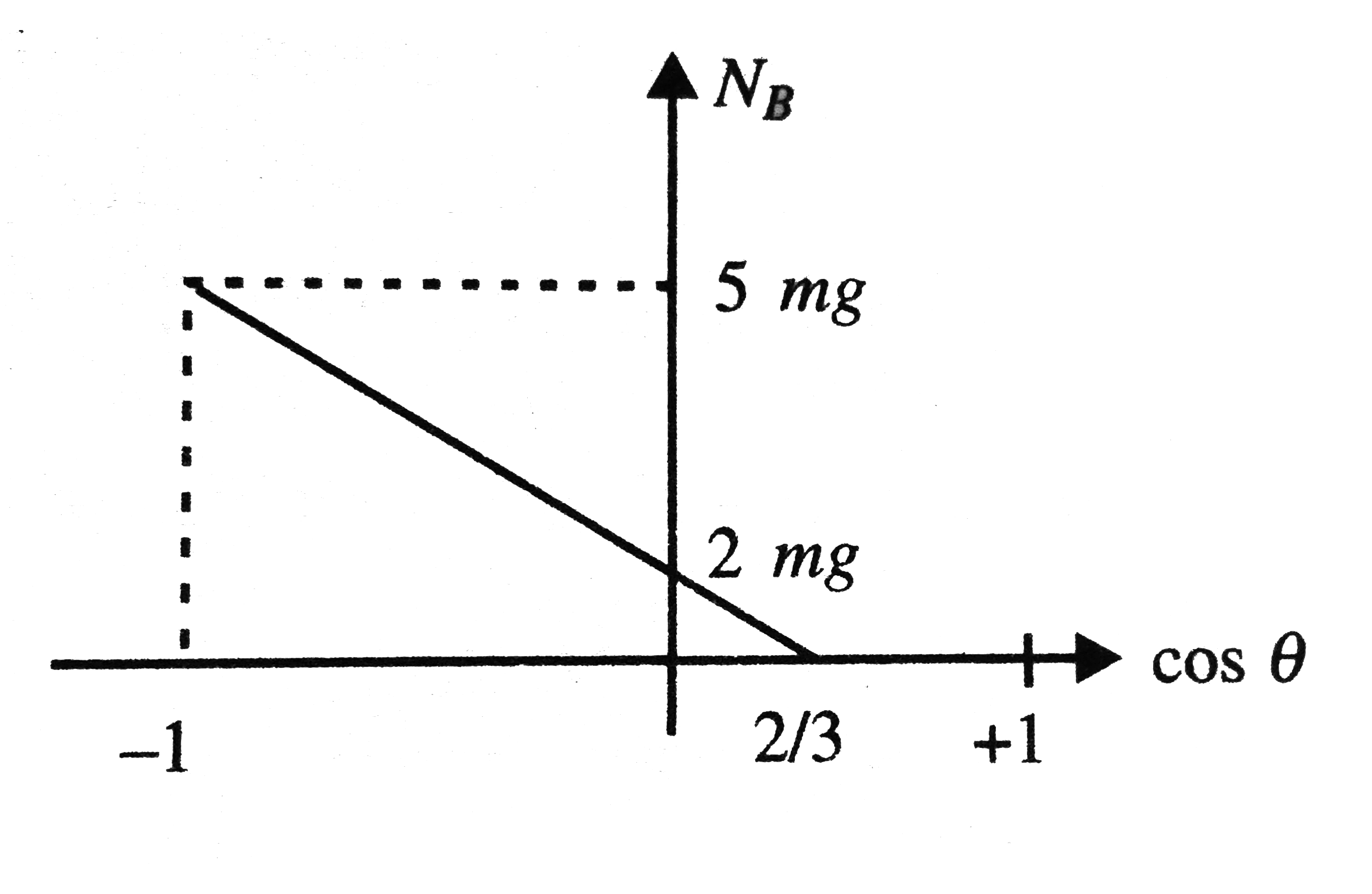
When cosθ=23, NB=0
When cosθ=−1, NB=5mg
Therefore, the graph is as shown in figure.
Topper's Solved these Questions
- WORK, POWER & ENERGYBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - WORK, POWER & ENERGYEXERCISE - Exercise 8.1
25 Videos
- WORK, POWER & ENERGYBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - WORK, POWER & ENERGYEXERCISE - Exercise 8.2
25 Videos
- WORK, POWER & ENERGYBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - WORK, POWER & ENERGYEXERCISE - Archives (integer)
4 Videos
- VECTORSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - VECTORSEXERCISE - Exercise Multiple Correct
5 Videos
Similar Questions
A small spherical ball of mass m is projected from lowest point (point P) in the space between two fixed, concentric spheres A and B (see figure). The smaller sphere A has a radius R and the space between the two spheres has a width d. The ball has a diameter very slightly less than d. All surfaces are frictionless. Speed of ball at lowest point is v. NA and NB represent magnitudes of the normal reaction force on the ball exerted by the spheres A and B respectively. Match the value of v given in column–I with corresponding results in column–II.

View SolutionA sphere with diameter 10 meters is inscribed in a cube .What is the volume of the space between the sphere and the cube ?
View Solution
Knowledge Check
Find the moment of inertia of a sphere about a tangent to the sphere, while the mass of the sphere is M and the radius of the sphere is R.
A25MR2B65MR2C45MR2D75MR2
A sphere of mass m held at a height 2R between a wedge of same m and a rigid wall, is released from, Assuming that all the surfaces are frictionless. Find the speed of the bodies when the sphere hits the ground.
 .
.
View SolutionFind the moment of inertia of a sphere about a tangent to the sphere, while the mass of the sphere is M and the radius of the sphere is R.
View SolutionA sphere of mass M rolls without slipping on rough surface with centre of mass has constant speed v0. If mass of the sphere is m and its radius be R, then the angular momentum of the sphere about the point of contact is.
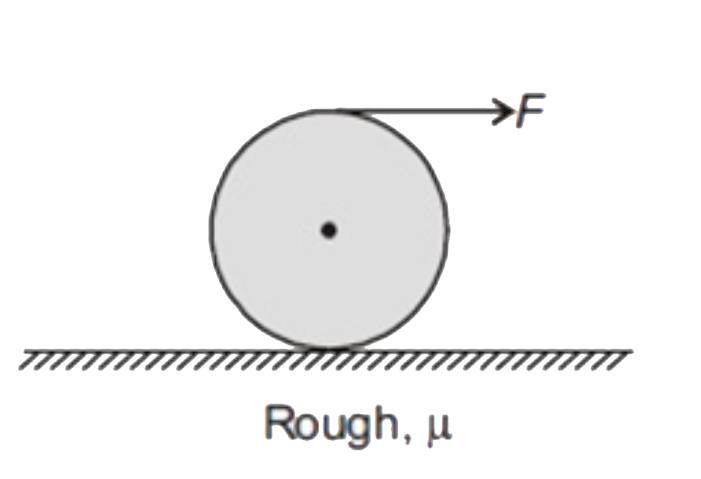
View SolutionA solid sphere of mass M and radius R is pulled by a force F as shown in figure . If the sphere does not slip over the surface , then frictional force acting on the sphere is
View SolutionA spherical condenser has innder and outer spheres of radii a and b respectively. The space between the two is filled with air. The difference between the capacities of two condensers formed when outer sphere is earthed and when inner sphere is earthed will be
View SolutionA solid metal sphere of radius R has a charg +2Q. A hollow spherical shell of radius 3R placed concentric with the frist sphere has net charge -Q.
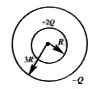
What would be the final distribution of charges if the sphres are joined by a conducting wire
View SolutionA conducting sphere of radius r has a charge . Then .
View Solution
