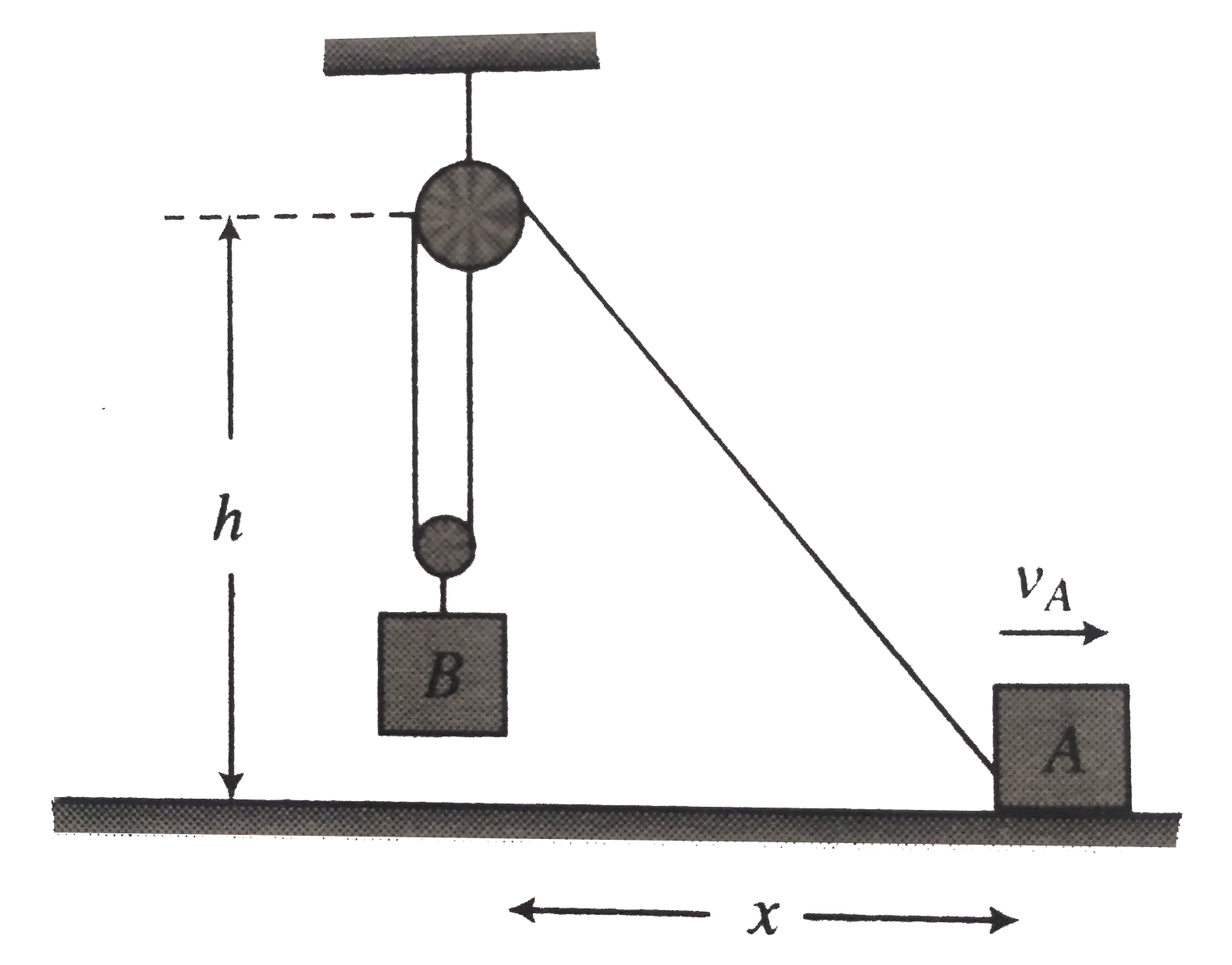
If block A is moving horizontally with velocity vA, then find the velocity of block B at the instant as shown in fig.
hvA2√x2+h2
xvA√x2+h2
xvA2√x2+h2
hvA√x2+h2
The correct Answer is:C
From fig., L=2h−2y+√x2+h2
Differentiating the equation, we get
dydt=x2√h2+x2ddt
⇒VB=xVA2√h2+x2
Topper's Solved these Questions
- NEWTON'S LAWS OF MOTION 1BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - NEWTON'S LAWS OF MOTION 1EXERCISE - Multiple Correct
11 Videos
- NEWTON'S LAWS OF MOTION 1BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - NEWTON'S LAWS OF MOTION 1EXERCISE - Assertion-reasoning
15 Videos
- NEWTON'S LAWS OF MOTION 1BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - NEWTON'S LAWS OF MOTION 1EXERCISE - Subjective
15 Videos
- MISCELLANEOUS VOLUME 2BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - MISCELLANEOUS VOLUME 2EXERCISE - INTEGER_TYPE
10 Videos
- NEWTON'S LAWS OF MOTION 2BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - NEWTON'S LAWS OF MOTION 2EXERCISE - Integer type
1 Videos
Similar Questions
The velocity of the block B is:

View SolutionThe block A is moving downward with constant velocity v0. Find the velocity of the block B. When the string makes an angle θ with the horizontal

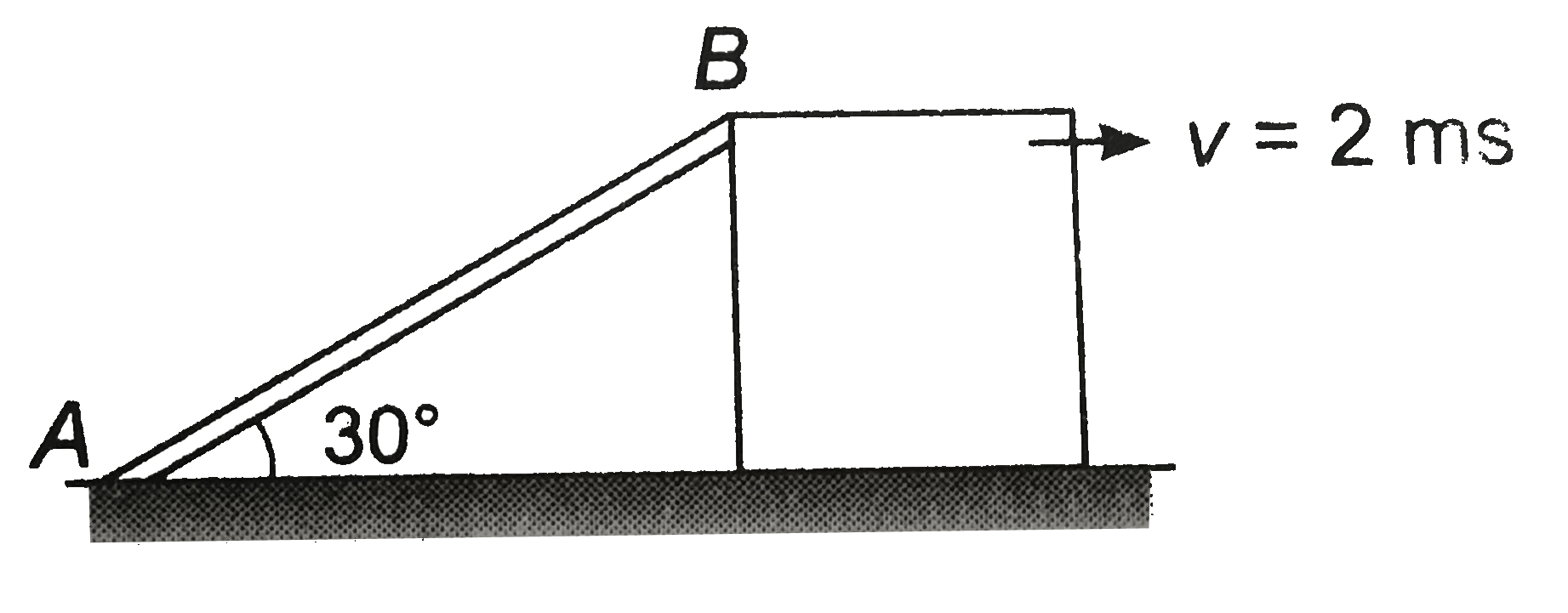
View SolutionA rod AB is shown in figure. End A of the rod is fixed on the ground. Block is moving with velocity 2ms−1 towards right. The velocity of end B of rod at the instant shown in figure is
View SolutionAn inextensible string AB is tied to a block B of negligible dimensions and passes over a small pulley C so that free end A hangs h unit above the ground on which the block B rests. In this initial position shown in fig. The free end A is h unit below C. if now end A moves horizontally with a velocity v0, obtain an expression for the velocity of the block at any time t.

View SolutionA disc of radius R is moving on a rough horizontal surface with velocity v and angular speed ω at an instant as shown in figure. Choose the correct statement.

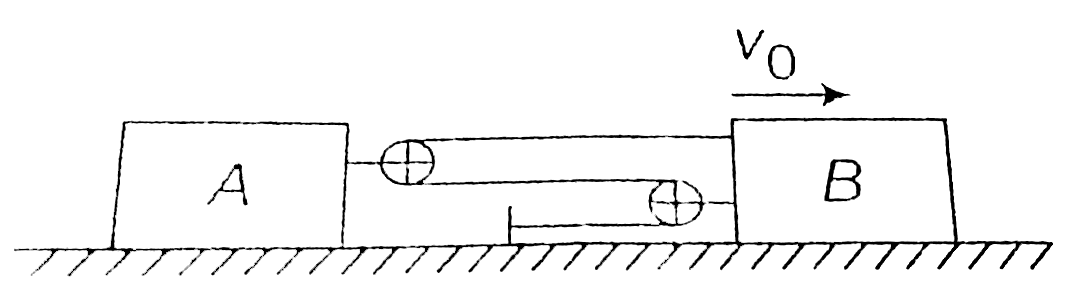
View SolutionBlock B moves to the right with a constant velocity v0. The velocity of body a relative to b is
View SolutionFind the angular velocity of A with respect to O at the instant shown in (Fig. 5.165).
 .
.
View SolutionThe block shown is moving with constant velocity. Find μk between the block and the surface.
View SolutionA block of mass m moving with velocity v0 on a smooth horizontal surface hits the spring of constant k as shown. The maximum compression in spring is

View SolutionIn the system shown, the block A is moving down eith velocity v1 and C is moving up with velocity v3. Express velocity of the block B in terms of velocities of the blocks a and C.

View Solution
