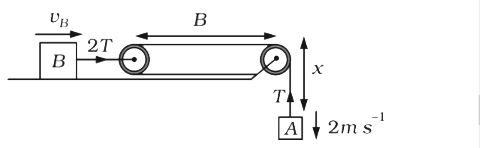
The velocity of the block B is:

2ms−1
3ms−1
1ms−1
6ms−1
The correct Answer is:C
x + 2y = L (length of string)
dxdt+2dydt=0⇒−dydt=12(dxdt)vB=12(2)=1ms−1
Applying tension trick,
2T(VB)−T(2)=0⇒2T(VB)=2T∴VB=1ms−1
Topper's Solved these Questions
- DYNAMICS OF A PARTICLEBOOK - VMC MODULES ENGLISHCHAPTER - DYNAMICS OF A PARTICLEEXERCISE - LEVEL 2
49 Videos
- DYNAMICS OF A PARTICLEBOOK - VMC MODULES ENGLISHCHAPTER - DYNAMICS OF A PARTICLEEXERCISE - LEVEL 2 ( NUMERICAL TYPE FOR JEE MAIN )
16 Videos
- DYNAMICS OF A PARTICLEBOOK - VMC MODULES ENGLISHCHAPTER - DYNAMICS OF A PARTICLEEXERCISE - LEVEL 0 (LONG ANSWER TYPE)
4 Videos
- DC CIRCUITBOOK - VMC MODULES ENGLISHCHAPTER - DC CIRCUITEXERCISE - JEE ADVANCED ARCHIVE
68 Videos
- ELECTROMAGNETIC INDUCTION & ALTERNATING CURRENTBOOK - VMC MODULES ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTION & ALTERNATING CURRENTEXERCISE - IN-CHAPTER EXERCISE-G
10 Videos
Similar Questions
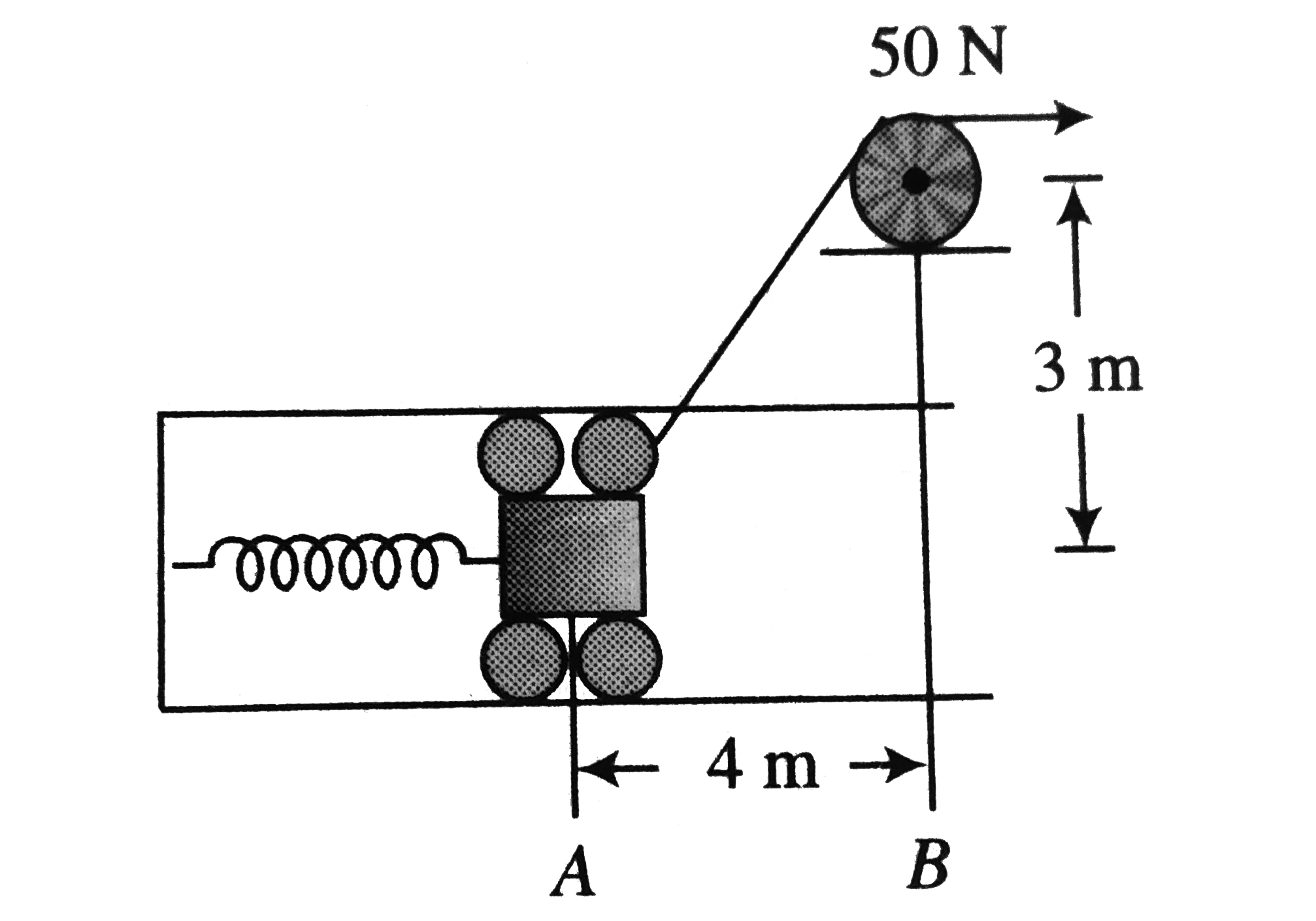
A 20−kg block attached to a spring of spring constant 5Nm−1 is released from rest at A. The spring at this instant is having an elongation of 1m. The block is allowed to move in smooth horizontal slot with the help of a constant force 50N in the rope as shown. The velocity of the block as it reaches B is (assume the rope to be light)
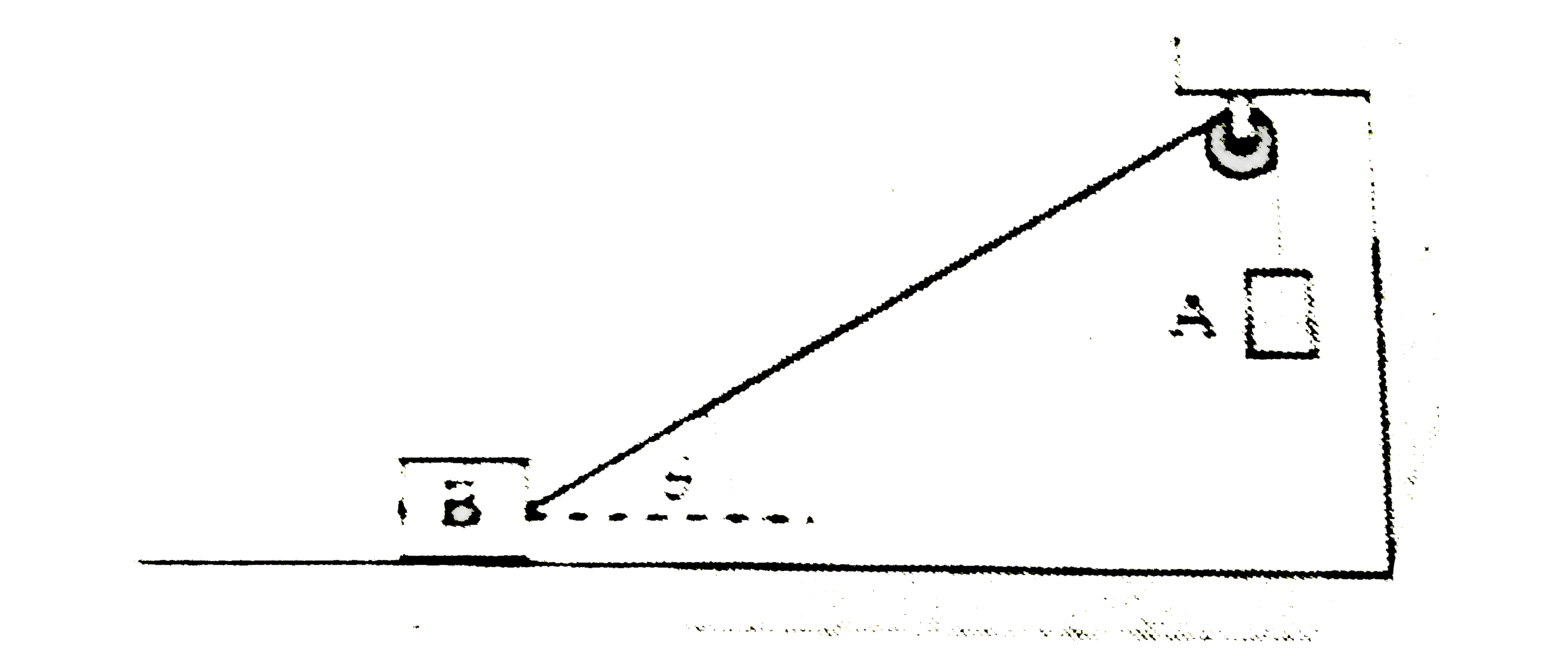
View SolutionThe block A is moving downward with constant velocity v0. Find the velocity of the block B. When the string makes an angle θ with the horizontal
View Solution
Knowledge Check
The figure above shows the two unbalanced forces acting on a block. If the velocity of the block is to the left, then
AThe work done by F1 is positiveBThe work done by F2 is negativeCThe momentum of the block is decreasingDthe net force is in the same direction as the velocityA small block of mass M moves on a friction-less surface of an inclined plane, as shown in the figure. The angle of the incline suddenly changes from 60∘ to 30∘ at point B. The block is initially at rest at A.
If collision between the block and the incline is completely elastic, then the vertical (upward) component of the velocity of the blocks at point B, immediately after it strikes the second incline is
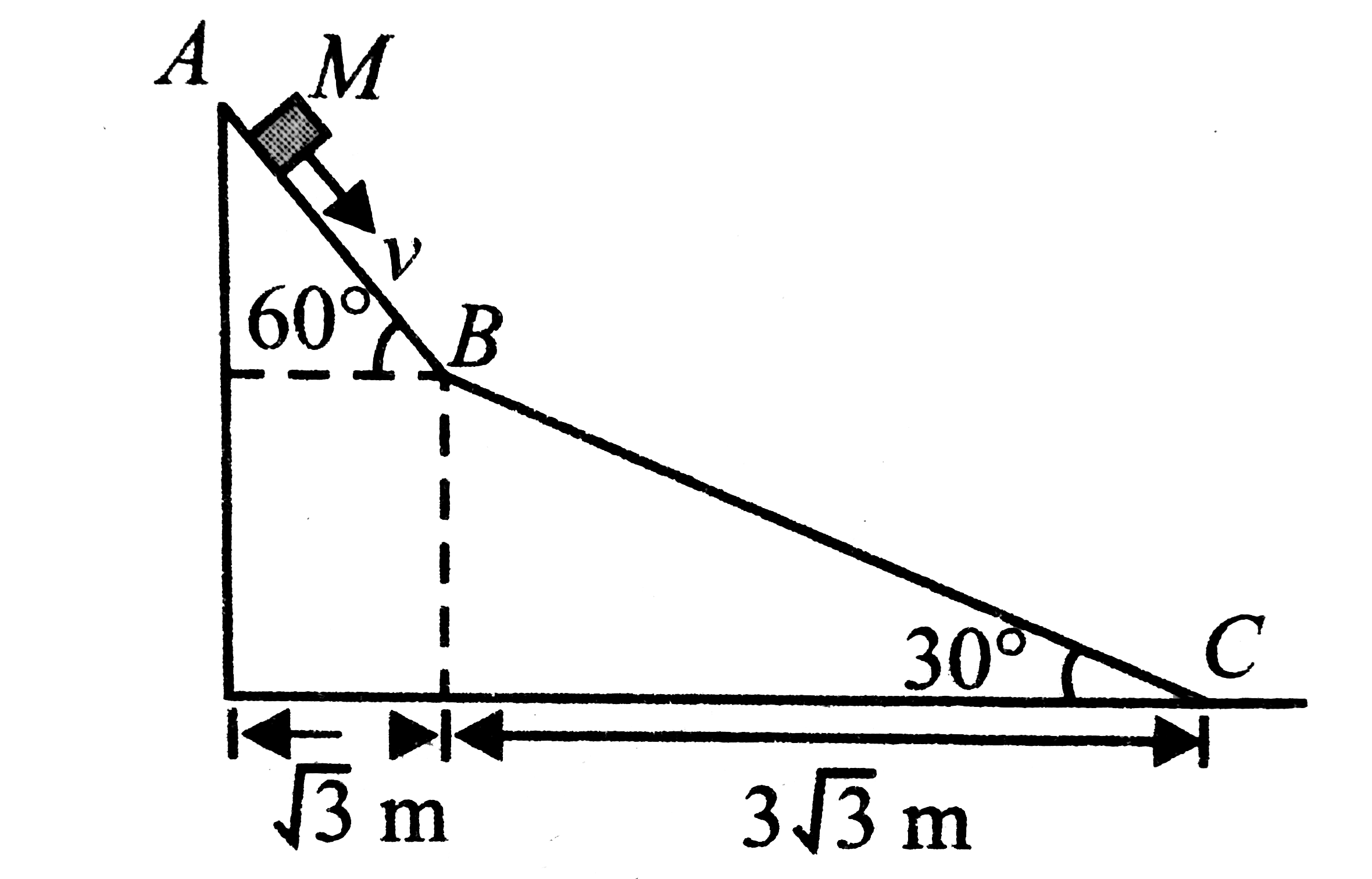 A√30 m/sB√15 m/sC0D−√15 m/s
A√30 m/sB√15 m/sC0D−√15 m/s
In the system shown, the block A is moving down eith velocity v1 and C is moving up with velocity v3. Express velocity of the block B in terms of velocities of the blocks a and C.
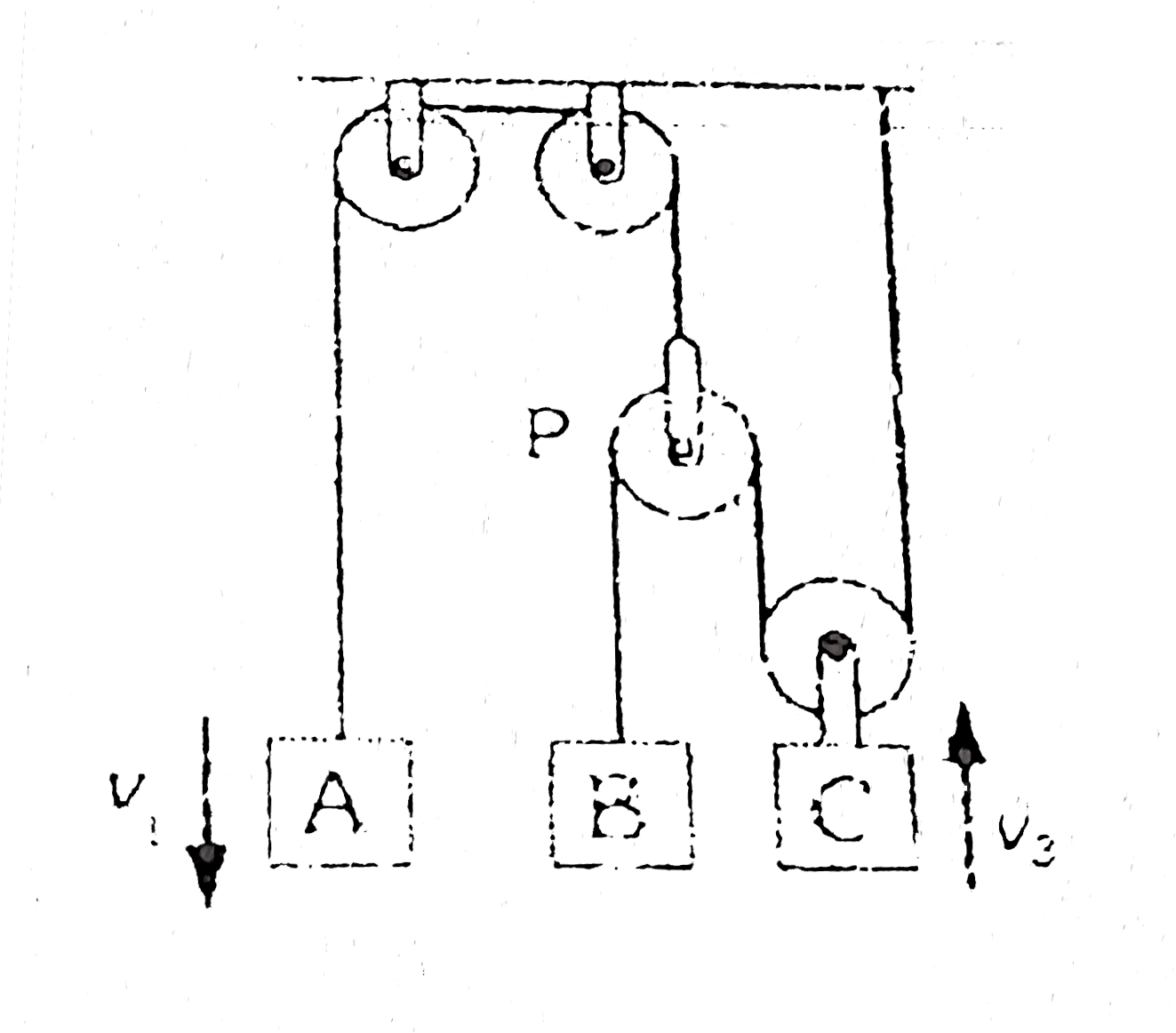
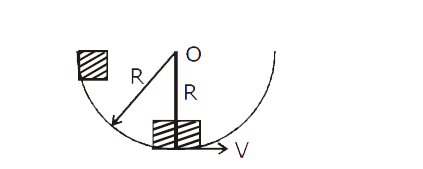
View SolutionA block of mass m slides down along the surface of the bowl from the rim to the bottom as shown in fig. The velocity of the block at the bottom will be-
View SolutionA small block of mass m is released from a fixed smooth wedge in figure. Initial point is marked as A. Bottom of wedge is marked as B and at a point C the block stops because the straight part of floor is rough.
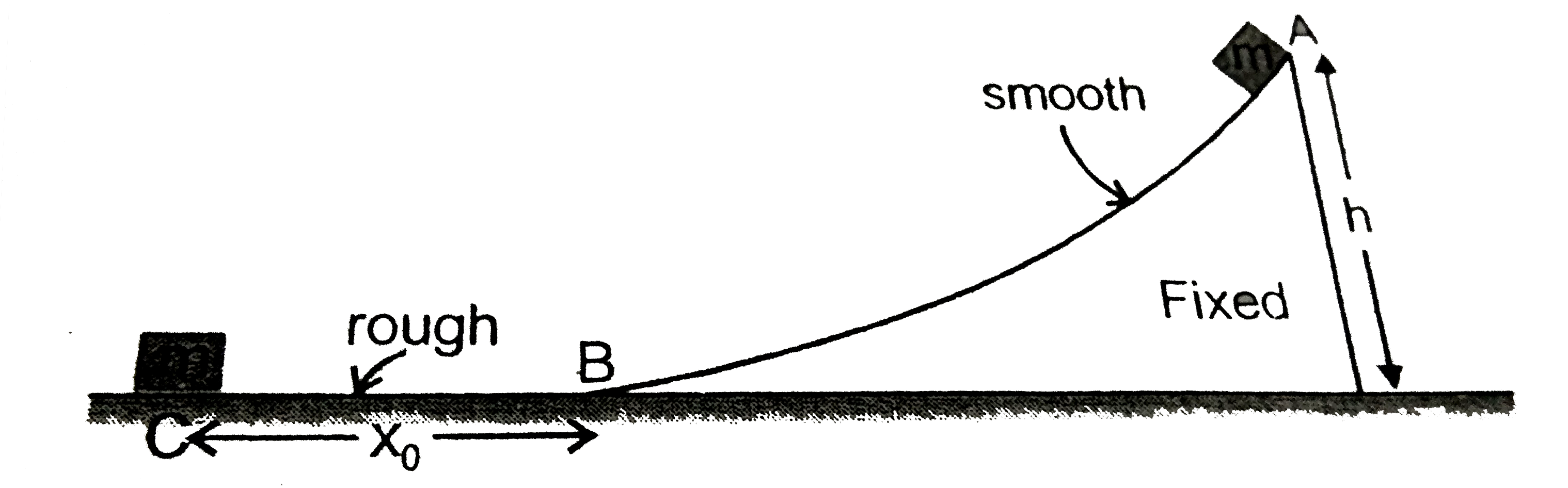
The velocity of the block at the midpoint between B to C will be :
View SolutionA moving block having mass m , collides with another stationary block having mass 4m. The lighter block comes to rest after collision. When the initial velocity of the block is v, then the value of coefficient of restitution (e) will be
View SolutionTwo blocks A and B of mass m and 2m respectively are moving towards a massive (mass>>2m) cliff with velocities 2v and v respectively. The cliff moves with a velocity v. If the coefficient of restitution of collision at the surface of the cliff is e=1/2, find the:

a. velocity of the block B just after colliding with the cliff.
b. work done by the cliff during collision.
c. maximum compression of the spring of stiffness k which is fitted with the block B.
View SolutionA block is gently placed on a conveyor belt moving horizontal with constant speed After t=4s the velocity of the block becomes equal to velocity of the belt If the coefficient of friction between the block and the belt is μ=0.2, then the velocity of the conveyor belt is .
View Solution
