A block is gently placed on a conveyor belt moving horizontal with constant speed After t=4s the velocity of the block becomes equal to velocity of the belt If the coefficient of friction between the block and the belt is μ=0.2, then the velocity of the conveyor belt is .
8ms−1
4ms−1
6ms−1
18ms−1
The correct Answer is:A
To solve the problem, we need to analyze the motion of the block placed on the conveyor belt. Here’s a step-by-step breakdown of the solution:
Step 1: Understanding the Problem
The block is placed on a conveyor belt that is moving with a constant speed. Initially, the block is at rest relative to the ground. The block starts to accelerate due to the friction between it and the conveyor belt until its velocity matches that of the belt after a time t=4seconds.
Step 2: Identify the Forces Acting on the Block
The only horizontal force acting on the block is the frictional force, which provides the necessary acceleration for the block to catch up with the conveyor belt. The frictional force can be expressed as:
\( F_f = \mu \cdot m \cdot g \)
where:
- \( \mu = 0.2 \) (coefficient of friction)
- \( m \) is the mass of the block (which we will see cancels out)
- \( g = 10 \, \text{m/s}^2 \) (acceleration due to gravity)
Step 3: Calculate the Acceleration of the Block
The acceleration \( a \) of the block can be calculated from the frictional force:
\( a = \frac{F_f}{m} = \frac{\mu \cdot m \cdot g}{m} = \mu \cdot g \)
Substituting the values:
\( a = 0.2 \cdot 10 = 2 \, \text{m/s}^2 \)
Step 4: Use the Kinematic Equation
Since the block starts from rest, we can use the kinematic equation to find the final velocity \( v \) of the block after time \( t = 4 \, \text{s} \):
\( v = u + at \)
where:
- \( u = 0 \) (initial velocity of the block)
- \( a = 2 \, \text{m/s}^2 \)
- \( t = 4 \, \text{s} \)
Substituting the values:
\( v = 0 + (2 \cdot 4) = 8 \, \text{m/s} \)
Step 5: Conclusion
The final velocity of the block after 4 seconds is equal to the velocity of the conveyor belt, which is:
\( v = 8 \, \text{m/s} \)
Thus, the velocity of the conveyor belt is 8 m/s.
---
The block is placed on a conveyor belt that is moving with a constant speed. Initially, the block is at rest relative to the ground. The block starts to accelerate due to the friction between it and the conveyor belt until its velocity matches that of the belt after a time t=4seconds.
The only horizontal force acting on the block is the frictional force, which provides the necessary acceleration for the block to catch up with the conveyor belt. The frictional force can be expressed as:
\( F_f = \mu \cdot m \cdot g \)
where:
- \( \mu = 0.2 \) (coefficient of friction)
- \( m \) is the mass of the block (which we will see cancels out)
- \( g = 10 \, \text{m/s}^2 \) (acceleration due to gravity)
The acceleration \( a \) of the block can be calculated from the frictional force:
\( a = \frac{F_f}{m} = \frac{\mu \cdot m \cdot g}{m} = \mu \cdot g \)
Substituting the values:
\( a = 0.2 \cdot 10 = 2 \, \text{m/s}^2 \)
Since the block starts from rest, we can use the kinematic equation to find the final velocity \( v \) of the block after time \( t = 4 \, \text{s} \):
\( v = u + at \)
where:
- \( u = 0 \) (initial velocity of the block)
- \( a = 2 \, \text{m/s}^2 \)
- \( t = 4 \, \text{s} \)
\( v = 0 + (2 \cdot 4) = 8 \, \text{m/s} \)
The final velocity of the block after 4 seconds is equal to the velocity of the conveyor belt, which is:
\( v = 8 \, \text{m/s} \)
Topper's Solved these Questions
- LAWS OF MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - LAWS OF MOTIONEXERCISE - Chapter exercises (A) Taking it together
71 Videos
- LAWS OF MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - LAWS OF MOTIONEXERCISE - Match the columns
7 Videos
- LAWS OF MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - LAWS OF MOTIONEXERCISE - Check point 5.3
20 Videos
- KINEMATICS 1BOOK - DC PANDEY ENGLISHCHAPTER - KINEMATICS 1EXERCISE - INTEGER_TYPE
15 Videos
- LAWS OF THERMODYNAMICSBOOK - DC PANDEY ENGLISHCHAPTER - LAWS OF THERMODYNAMICSEXERCISE - Level 2 Subjective
18 Videos
Similar Questions
A block is gently placed on a conveyor belt moving horizontally with constant speed. After t = 4s, the velocity of the block becomes equal to the velocity of the belt. If the coefficient of friction between the block and the belt is μ=0.2, then the velocity of the conveyor belt is (g=10ms−2)
View SolutionA block of mass m is placed at rest on an inclination θ to the horizontal. If the coefficient of friction between the block and the plane is μ, then the total force the inclined plane exerts on the block is
View Solution
Knowledge Check
A block slides with a velocity of 10 m/sec. on a rough horizontal surface. It comes to rest after covering of 50 m. If g is 10 m/sec2, then the coefficient of dynamic friction between the block and surface is
A1B10C2D0.1
A block of mass m is gently placed over a massive plank moving horizontal over a smooth surface with velocity 10ms−1. The coefficient of friction between the block and the plank is 0.2. The distance travelled by the block till it slides on the plank is [g=10ms−2]
View SolutionA block of mass 4kg is placed on a rough horizontal plane A time dependent force F=kt2 acts on the block where k=2N/s2 Coefficient of friction μ=0.8 force of friction between the block and the plane at t=2s is
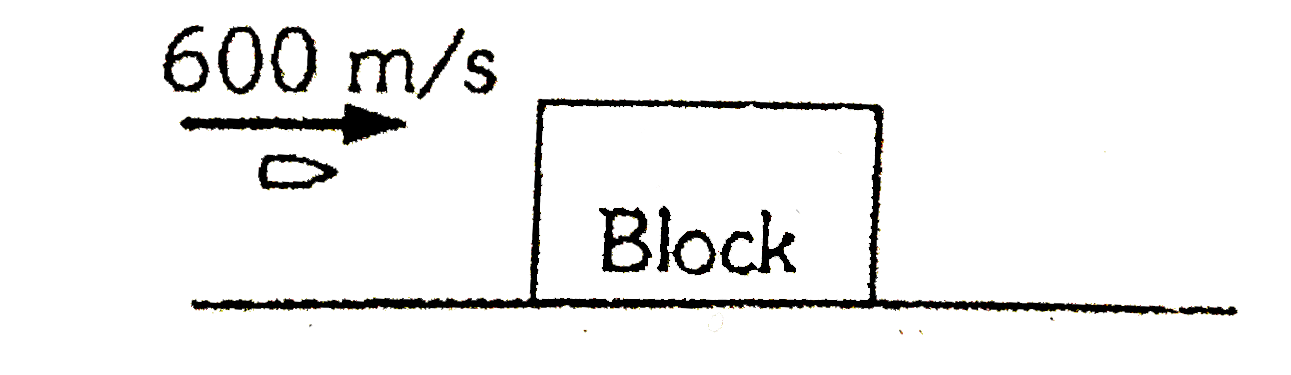
View SolutionA bullet of mass 50g moving with velocity 600m/s hits block of mass 1.0kg placed on a rough horizontal ground and comes out of the block with a velocity of 400m/s. The coefficient of friction between the block and the ground is 0.25. Neglect loss of mass of the block as the bullet pierces through it.
(a) In spite of the fact that friction acts a an external force, can you apply principle of conservation of momentum during interaction of the ullet with the block?
(b) Find velocity of the block immediately after the bullet pierces through it. (c)FInd the distance the block will travel before it stops.
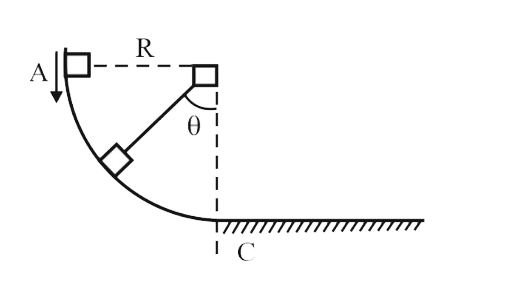
View SolutionA block of mass m is placed on a vertical fixed circular track and then it is given velocity v along the track at position A on track. The coefficient of friction between the block and the track varies with the angle θ . If the block moves on track with constant speed then the coefficient of friction is
View SolutionA block of mass m slides 0n a frictionless table. It is constrained to move inside a ring of radius R . At time t=0 , block is moving along the inside of the ring (i.e. in the tangential direction) with velocity v0 . The coefficient of friction between the block and the ring is μ . Find the speed of the block at time t .

View SolutionA block of mass m is moving on a rough horizontal surface. μ is the coefficient of kinetic friction between the block and the surface. What is the net force exerted by the surface on the block?
View SolutionA block of mass 9 kg is lying on a rough horizontal surface. A particle of mass 1kg strikes the block with a speed of 50m/s at an angle of 37∘ with the vertical and sticks to it. The frictional coefficient between the ground and the block is μ=0.4. Find the velocity of the combined system just after the collision assuming limiting friction coefficient between the block and the ground after the collision ?
View Solution
