A block of mass 4kg is placed on a rough horizontal plane A time dependent force F=kt2 acts on the block where k=2N/s2 Coefficient of friction μ=0.8 force of friction between the block and the plane at t=2s is
8 N
4 N
2 N
32 N
The correct Answer is:A
To solve the problem step by step, we will follow these calculations:
Step 1: Calculate the applied force at t=2s
The applied force F is given by the equation:
F=kt2
where k=2N/s2 and t=2s.
Substituting the values:
F=2×(22)=2×4=8N
Step 2: Calculate the normal force acting on the block
The normal force N acting on the block is equal to the weight of the block, which can be calculated using:
N=mg
where m=4kg and g=10m/s2.
Substituting the values:
N=4×10=40N
Step 3: Calculate the maximum (limiting) frictional force
The maximum frictional force fmax can be calculated using the formula:
fmax=μN
where μ=0.8.
Substituting the values:
fmax=0.8×40=32N
Step 4: Compare the applied force with the maximum frictional force
Now we compare the applied force F=8N with the maximum frictional force fmax=32N.
Since F<fmax, the block will not slide, and the frictional force will equal the applied force.
Step 5: Determine the frictional force acting on the block
Since the block is in equilibrium and the applied force is less than the maximum frictional force, the frictional force f will be equal to the applied force:
f=F=8N
Final Answer
The force of friction between the block and the plane at t=2s is 8N.
---
F=kt2
where k=2N/s2 and t=2s.
F=2×(22)=2×4=8N
N=mg
where m=4kg and g=10m/s2.
N=4×10=40N
fmax=μN
where μ=0.8.
fmax=0.8×40=32N
f=F=8N
Topper's Solved these Questions
- LAWS OF MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - LAWS OF MOTIONEXERCISE - Chapter exercises (A) Taking it together
71 Videos
- LAWS OF MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - LAWS OF MOTIONEXERCISE - Match the columns
7 Videos
- LAWS OF MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - LAWS OF MOTIONEXERCISE - Check point 5.3
20 Videos
- KINEMATICS 1BOOK - DC PANDEY ENGLISHCHAPTER - KINEMATICS 1EXERCISE - INTEGER_TYPE
15 Videos
- LAWS OF THERMODYNAMICSBOOK - DC PANDEY ENGLISHCHAPTER - LAWS OF THERMODYNAMICSEXERCISE - Level 2 Subjective
18 Videos
Similar Questions
A block of mass 4kg is placed on a rough horizontal force plane. A time dependent horizontal force F=kt acts on the block. Here k=2Ns−1. The frictional force between the block and plane at time t=2s is (μ=0.2) a) 4 N b) 8 N c) 12 N d) 10 N
View SolutionA block is placed on a rough horizontal plane. A time dependent horizontal force F=K t acts on the block K is a postive constant. Accelration-time graph of the block is
View Solution
Knowledge Check
A block of mass 2 kg is placed on the floor. The coefficient of static friction is 0.4. A force F of 3 N is applied on the block as shown in figure. The force of friction between the block and the floor is (Take g=10ms−2)
 A3 NB8 NC4 ND6 N
A3 NB8 NC4 ND6 NA block of mass 2 kg is placed on the floor. The coefficient of static friction is 0.4. A force F of 2.5 N is applied on the block as shown in Fig. 15.4.4. The force of friction between the block and the floor is (g=9.8m/s2)
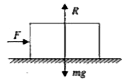 A1.5 NB0.5 NC2.5 NDNone of the above
A1.5 NB0.5 NC2.5 NDNone of the above
A block of mass 20kg is placed on a rough horizontal plane and a horizontal force of 12N is applied. If coefficient of friction is 0.1 the frictional force acting on it is,
View SolutionA block of mass 10 kg is placed on the rough horizontal surface. A pulling force F is acting on the block which makes an angle θ above the horizontal. If coefficient of friction between block and surface is 43 then minimum value of force required to just move the block is (g=10ms2)
View SolutionA block is sliding on a rough horizontal surface. If the contact force on the block is √2 times the frictional force, the coefficient of friction is
View SolutionA block of mass 4 kg is kept on a rough horizontal surface. The coefficient of static friction is 0.8. If a forace of 19 N is applied on the block parallel to the floor, then the force of friction between the block and floor is
View SolutionA block of mass 2 kg is kept on a rough horizontal floor an pulled with a force F. If the coefficient of friction is 0.5. then the minimum force required to move the block is :-

View SolutionA block of mass 2 kg is placed on the floor. The coefficient of static friction it 0.4. A force F of 2.5 N is applied on the block, as shown. calculate the force of friction between the block and the floor. (g=9.8m/s2).
View Solution
