A mass placed on an inclined place is just in equilibrium. If μ is coefficient of friction of the surface, then maximum inclination of the plane with the horizontal is
tan−1μ
tan−1(μ/2)
sin−1μ
cos−1μ
The correct Answer is:A
To solve the problem of finding the maximum inclination of an inclined plane with the horizontal when a mass is just in equilibrium, we can follow these steps:
1. Identify Forces Acting on the Mass:
- The weight of the mass (W = mg) acts vertically downward.
- This weight can be resolved into two components:
- Perpendicular to the inclined plane: W⊥=mgcosθ
- Parallel to the inclined plane: W∥=mgsinθ
2. Determine the Normal Force:
- The normal force (N) acting on the mass is equal to the perpendicular component of the weight:
N=mgcosθ
3. Calculate the Frictional Force:
- The frictional force (f) acting on the mass, which opposes the motion down the incline, is given by:
f=μN=μ(mgcosθ)
4. Set Up the Equilibrium Condition:
- For the mass to be in equilibrium, the net force acting parallel to the inclined plane must be zero. Therefore, we can set up the equation:
W∥−f=0
- Substituting the expressions for W∥ and f:
mgsinθ−μ(mgcosθ)=0
5. Simplify the Equation:
- Cancel mg from both sides (assuming m≠0):
sinθ=μcosθ
6. Rearrange to Find the Relationship:
- Dividing both sides by cosθ:
tanθ=μ
7. Find the Maximum Inclination Angle:
- To find the angle θ, take the inverse tangent:
θ=tan−1(μ)
Final Result:
Thus, the maximum inclination of the plane with the horizontal is:
θ=tan−1(μ)
- The weight of the mass (W = mg) acts vertically downward.
- This weight can be resolved into two components:
- Perpendicular to the inclined plane: W⊥=mgcosθ
- Parallel to the inclined plane: W∥=mgsinθ
- The normal force (N) acting on the mass is equal to the perpendicular component of the weight:
N=mgcosθ
- The frictional force (f) acting on the mass, which opposes the motion down the incline, is given by:
f=μN=μ(mgcosθ)
- For the mass to be in equilibrium, the net force acting parallel to the inclined plane must be zero. Therefore, we can set up the equation:
W∥−f=0
- Substituting the expressions for W∥ and f:
mgsinθ−μ(mgcosθ)=0
- Cancel mg from both sides (assuming m≠0):
sinθ=μcosθ
- Dividing both sides by cosθ:
tanθ=μ
- To find the angle θ, take the inverse tangent:
θ=tan−1(μ)
Thus, the maximum inclination of the plane with the horizontal is:
θ=tan−1(μ)
Topper's Solved these Questions
- LAWS OF MOTIONBook:DC PANDEY ENGLISHChapter:LAWS OF MOTIONExercise:Chapter exercises (A) Taking it together
Explore 71 Videos
- LAWS OF MOTIONBook:DC PANDEY ENGLISHChapter:LAWS OF MOTIONExercise:Match the columns
Explore 7 Videos
- LAWS OF MOTIONBook:DC PANDEY ENGLISHChapter:LAWS OF MOTIONExercise:Check point 5.3
Explore 20 Videos
- KINEMATICS 1Book:DC PANDEY ENGLISHChapter:KINEMATICS 1Exercise:INTEGER_TYPE
Explore 15 Videos
- LAWS OF THERMODYNAMICSBook:DC PANDEY ENGLISHChapter:LAWS OF THERMODYNAMICSExercise:Level 2 Subjective
Explore 18 Videos
Similar Questions
A cylinder of mass m radius R is spined to a clockwise angular velocity ωo and then gently placed on an inclined plane for which coefficient of friction μ=tanθ,θ is the angle of inclined plane with the horizontal. The centre of mass of cylinder will remain stationary for time

View SolutionAn inclined plane of angule a is fixed onto a horizontal turntable with its line of greater slope in same plane as a diameter of forntable .A small block is placed on the inclined plane a distance r from the axis the coefficient of fraction between the block and the inclined plane is μ The turntable along with incline plane spins about its axis with constant minimum angular velocity ω
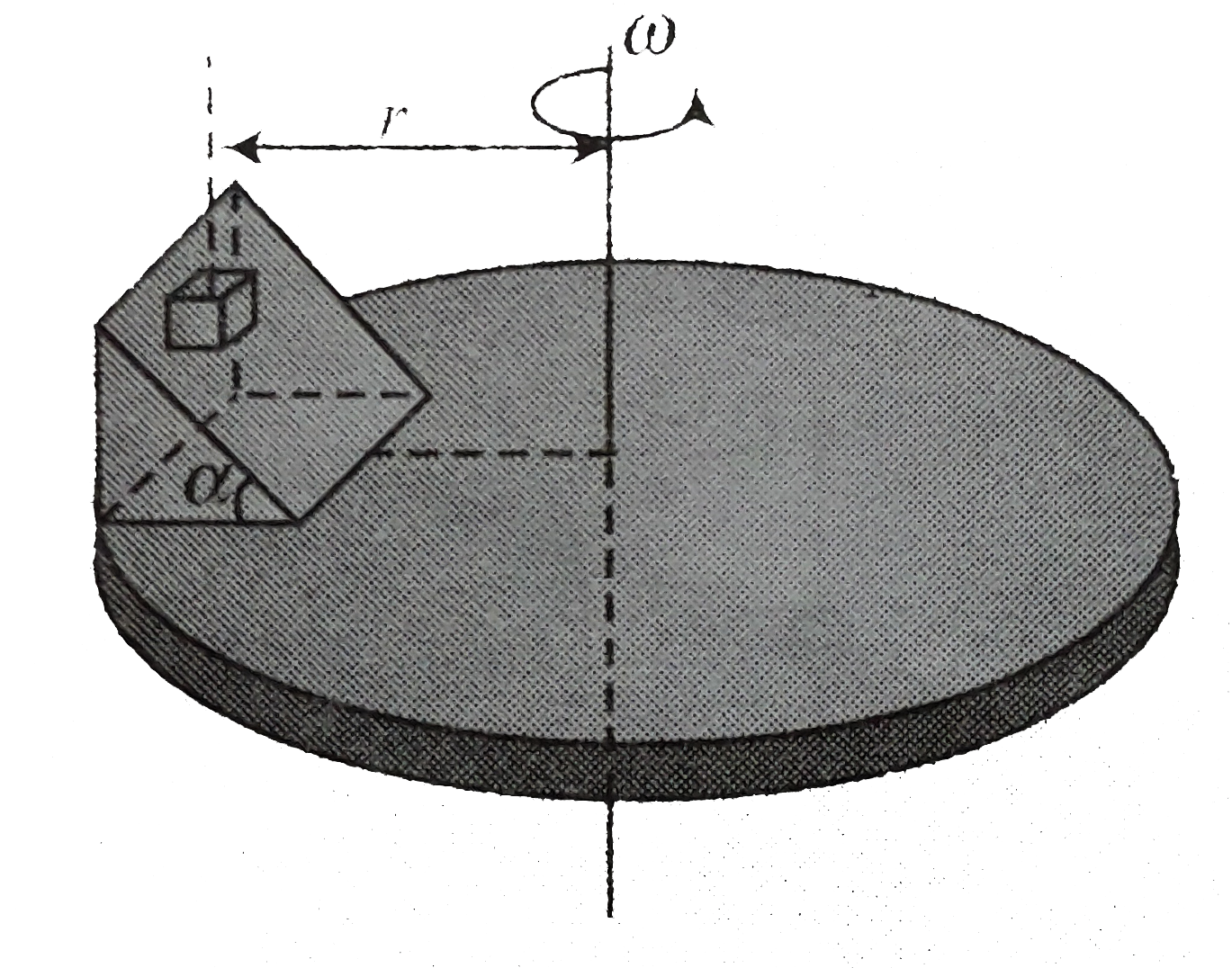
a. Find an capression for the minimum angular velocity ω to prevent the block from sliding down the plane in term of g,r,μ and the plane ω
b. Now a block of mass but having coefficient friction (with inclined plane)2μ is kept instead of the original block . find the radius of friction force acting between block and incline now to the friction force active in part (a)
View Solution
Knowledge Check
A block of mass m rests on a rough inclined plane. The coefficient of friction between the surface and the block is µ. At what angle of inclination θ of the plane to the horizontal will the block just start to slide down the plane?
Aθ=tan−1μBθ=cos−1μCθ=sin−1μDθ=sec−1μ
A block of mass m is placed at rest on an inclination θ to the horizontal. If the coefficient of friction between the block and the plane is μ, then the total force the inclined plane exerts on the block is
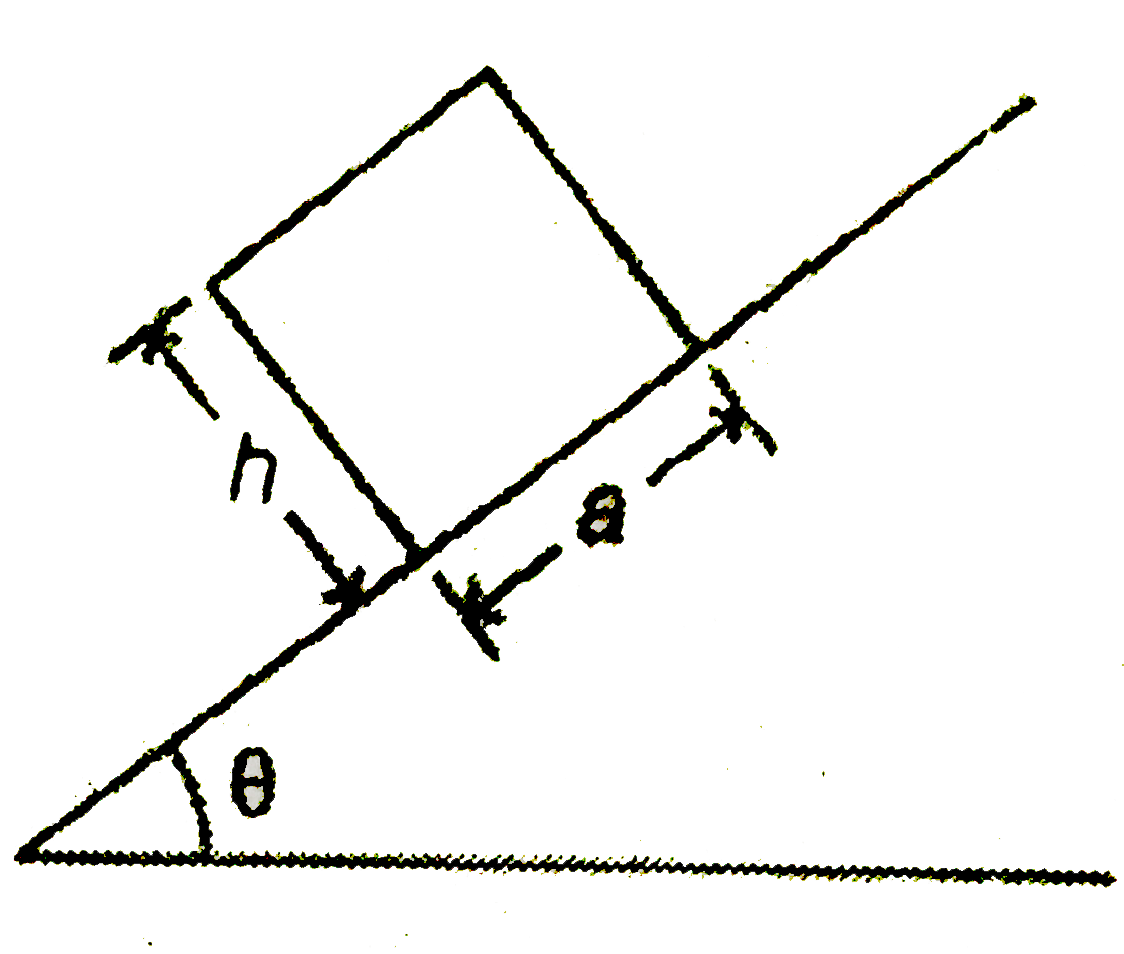
View SolutionA block with a square base measuring a×a and height h, is placed on an inclined plane. The coefficient of friction is μ. The angle of inclination (θ) of the plane is gradually increased. The block will
View SolutionA block of mass m is pulled on an incline surface having coefficient of friction μ=1& angle of inclination θ=30∘, with the horizontal, such that required external force is minimum. The angle made by this force with the incline is :
View SolutionA block of mass m is at rest on a rough inclined plane of angle of inclination θ. If coefficient of friction between the block and the inclined plane is μ, then the minimum value of force along the plane required to move the block on the plane is
View SolutionA block of mass m slides down an inclined plane of inclination θ with uniform speed. The coefficient of friction between the block and the plane is μ. The contact force between the block and the plane is
View SolutionA solid sphere of mass m is placed on a rough incline plane as shown in figure. The coefficient of friction (μ) is insufficient to start pure rolling. The sphere slides length l on incline from rest and its kinetic energy becomes k. Then work done by friction will be

View SolutionA block of mass m is placed on a rough plane inclined at an angle θ with the horizontal. The coefficient of friction between the block and inclined plane is μ . Ifθ<tan−1(μ) , then net contact force exerted by the plane on the block is :
View Solution
