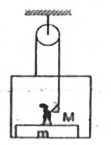
In fig. man A is standing on a movable plank while man B is standing on a stationary platform. Both are pulling the string down such that the plank moves slowly up. As a result of this the string slops through the hands of the men, find the ratio of length of the string that slips through the hands of A and B.

3/2
3/4
4/3
2/3
The correct Answer is:C
Let the plank move up by x, then pulley 2 will move down by x. Let the end of string C moves down by a distance y.
Let the initial length of string passing over pulley 2,
l1+l2…(i)
After displacements x and y mentioned above, the lengths become
(l1−2x)+(l2+y−x) ..(ii)
Equating Eqs. (i) and (ii), we get y=3x
Length of string that slips through A is y+x=4x and through B is y=3x.
Required ratio=4x3x=43

Topper's Solved these Questions
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - NEWTON'S LAWS OF MOTION 1EXERCISE - Multiple Correct11videos
NEWTON'S LAWS OF MOTION 1
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - NEWTON'S LAWS OF MOTION 1EXERCISE - Assertion-reasoning15videos
NEWTON'S LAWS OF MOTION 1
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - NEWTON'S LAWS OF MOTION 1EXERCISE - Subjective15videos
NEWTON'S LAWS OF MOTION 1
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - MISCELLANEOUS VOLUME 2EXERCISE - INTEGER_TYPE10videos
MISCELLANEOUS VOLUME 2
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - NEWTON'S LAWS OF MOTION 2EXERCISE - Integer type1videos
NEWTON'S LAWS OF MOTION 2
Similar Questions
A man of mass M stands at one end of a stationary plank of length L, lying on a smooth surface. The man walks to the other end of the plank. If the mass of the plank is M/3, the distance that the man moves relative to the ground is
View SolutionA man of mass M stands at one end of a stationary plank of length L, lying on a smooth surface. The man walks to the other end of the plank. If the mass of the plank is M/3, the distance that the man moves relative to the ground is
View SolutionA string of negligible thicknes is wrapped several times around a cylinder kept on a rough horizontal surface. A man standing at a distance l from the cylinder holds one end of the sitting an pulls the cylinder towards him figure. There is no slipping anywhere. The length of the string passed through the hand of the man whicle the cylinder reaches his hands is
 View Solution
View SolutionA man of mass M is standing on a plank kept in a box. The plank and box as a whole has mass m. A light string passing over a fixed smooth pulley connects the man and box. If the box remains stationary, find the tension in the string and the force exerted by the man on the plank.
 View Solution
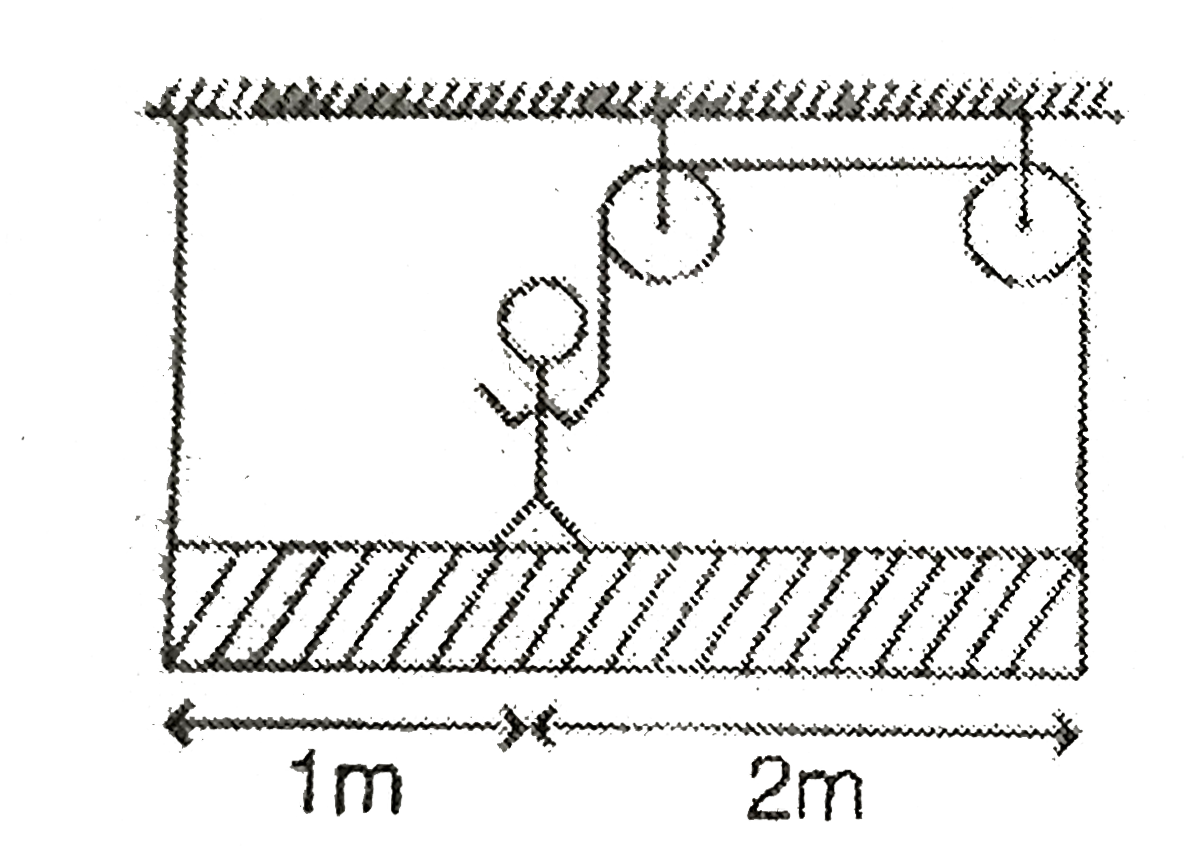
View SolutionA system consisting of a man on platfrom is in equilibrium. Masses of man and platiform are equal. The platform is in equilibrium due to two massless string is pulled by man resting on platform. Find the ratio of tension in left string to the tension in right string.
 View Solution
View SolutionA man of mass 62 kg is standing on a stationary boat of mass 238 kg. The man is carrying a sphere of mass 0.5 kg in his hands. If the man throws the sphere horizontally with a velocity of 12 ms−1, find the velocity with which the boat will move (in magnitude)
View SolutionFigure shows a mass m placed on a frictionless horizontal table and attached toa string passing through a mall hole in the surface. Initially, themas movesin a circle of radius r0 with a speed v0 and the ree end of the string is held by a person. The person pulls on the string slowly to decrease the radius of th circle of r. a. Find the tension in the string when the mass moves in the circle of radius r. b. Calculate the chasnge in the kinetic energy of the mass
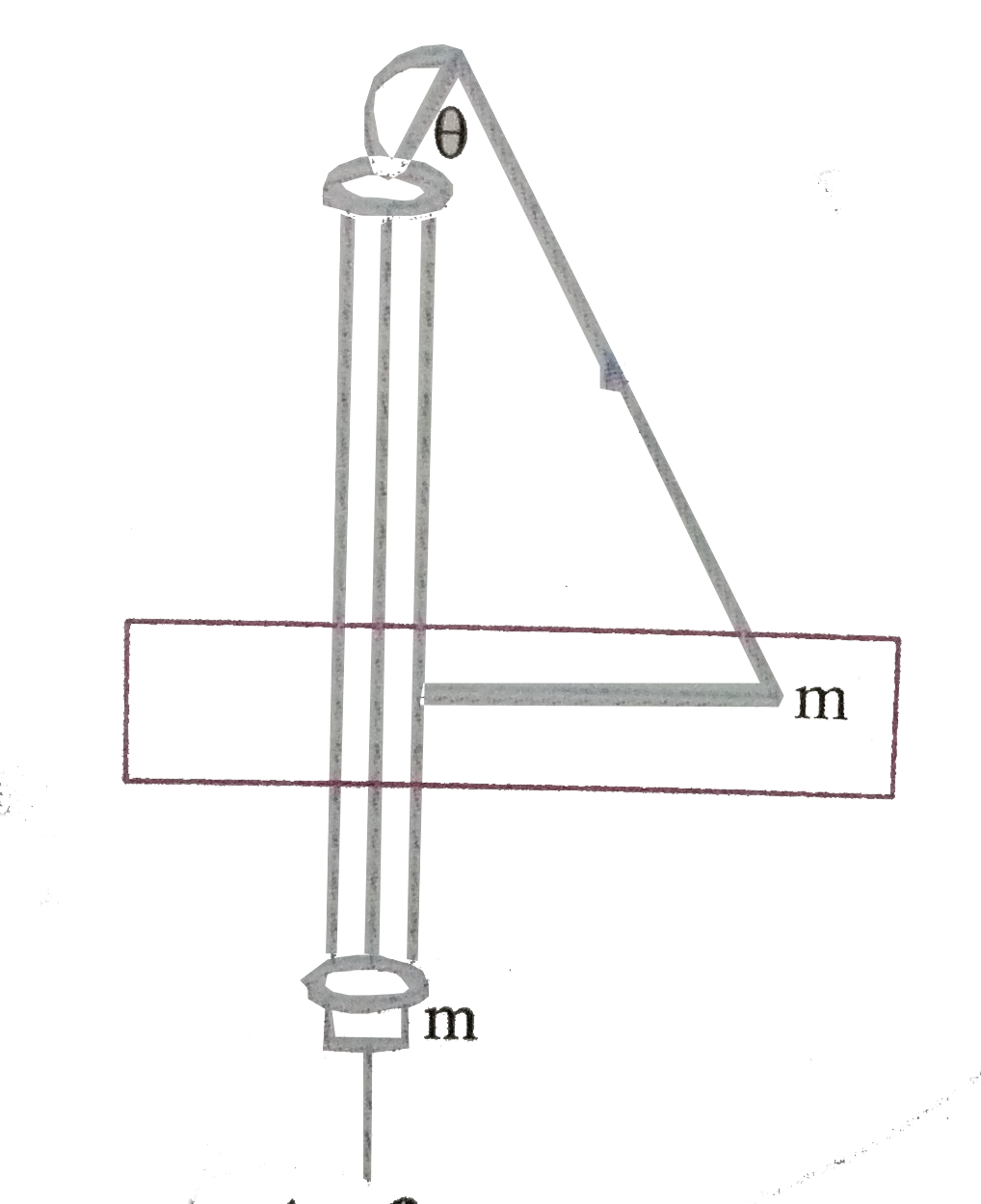
View SolutionA large mass M and a small mass m hang at the two ends of string that passes through a smooth tube as shown in fig. The mass m moves around in a circular path which lies in a horizantal plane. The length of the string from the mass m to the top of the tube is of length l and θ is the angle this length makes with the vertical, what should be the frequency of rotation of the mass m so that M remains stationary if M=16kg,m=4kg,l=1m and g=π2m/s2
 View Solution
View SolutionTwo men 'A' and 'B' are standing on a plank. 'B' is at the middle of the plank and 'A' is at the left end of the plank. Lower surface of the plank is smooth. System is initially at rest and masses are as shown in Fig. 'A' and 'B' start moving such that the position of 'B' remains fixed with respect to ground, then 'A' meets 'B'. Then the point where A meets B is located at
 View Solution
View SolutionA plank of mas M and length L is at rest on as frictionless floor. The top surface of the plank has friction. At one end of it a man of mass m is standing as shown in figure. If the man walks towards the other end the find the distance, which the plank moves a till the man reaches the centre of the plank. b. till the man reaches the other end of the plank.
 View Solution
View Solution
