Inside a horizontal moving box, an experimenter finds that when an object is placed on a smooth horizontal table and is released, it moves with an acceleration of , in this box. If 1-kg body is suspended with a light string. The tension in the string in equilibrium position. (w.r.t. experimenter) will be (take )
Zero
The correct Answer is:B
To solve the problem, we need to analyze the forces acting on the 1-kg body suspended by a light string inside the moving box.
1. Identify the Forces Acting on the Suspended Body:
- The body experiences two main forces: the gravitational force acting downward and the tension in the string acting upward.
- The gravitational force (weight) can be calculated using the formula:
Fg=m⋅g
where m=1kg and g=10m/s2.
2. Calculate the Weight of the Body:
Fg=1kg⋅10m/s2=10N
3. Consider the Pseudo Force:
- Since the box is accelerating horizontally with an acceleration a=10m/s2, a pseudo force acts on the suspended body in the opposite direction of the box's acceleration.
- The pseudo force Fp can be calculated as:
Fp=m⋅a=1kg⋅10m/s2=10N
4. Set Up the Equation for Tension:
- In the equilibrium position, the tension T in the string must balance both the gravitational force and the pseudo force. The forces can be represented in a right triangle where:
- One leg is the gravitational force (10 N downwards).
- The other leg is the pseudo force (10 N horizontally).
- Using Pythagoras theorem, the tension can be calculated as:
T=√F2g+F2p=√(10N)2+(10N)2
5. Calculate the Tension:
T=√100+100=√200=10√2N
Final Answer:
The tension in the string in the equilibrium position with respect to the experimenter is 10√2N.
- The body experiences two main forces: the gravitational force acting downward and the tension in the string acting upward.
- The gravitational force (weight) can be calculated using the formula:
Fg=m⋅g
where m=1kg and g=10m/s2.
Fg=1kg⋅10m/s2=10N
- Since the box is accelerating horizontally with an acceleration a=10m/s2, a pseudo force acts on the suspended body in the opposite direction of the box's acceleration.
- The pseudo force Fp can be calculated as:
Fp=m⋅a=1kg⋅10m/s2=10N
- In the equilibrium position, the tension T in the string must balance both the gravitational force and the pseudo force. The forces can be represented in a right triangle where:
- One leg is the gravitational force (10 N downwards).
- The other leg is the pseudo force (10 N horizontally).
- Using Pythagoras theorem, the tension can be calculated as:
T=√F2g+F2p=√(10N)2+(10N)2
T=√100+100=√200=10√2N
The tension in the string in the equilibrium position with respect to the experimenter is 10√2N.
Topper's Solved these Questions
- NEWTON'S LAWS OF MOTION 1Book:CENGAGE PHYSICS ENGLISHChapter:NEWTON'S LAWS OF MOTION 1Exercise:Multiple Correct
Explore 11 Videos
- NEWTON'S LAWS OF MOTION 1Book:CENGAGE PHYSICS ENGLISHChapter:NEWTON'S LAWS OF MOTION 1Exercise:Assertion-reasoning
Explore 15 Videos
- NEWTON'S LAWS OF MOTION 1Book:CENGAGE PHYSICS ENGLISHChapter:NEWTON'S LAWS OF MOTION 1Exercise:Subjective
Explore 15 Videos
- MISCELLANEOUS VOLUME 2Book:CENGAGE PHYSICS ENGLISHChapter:MISCELLANEOUS VOLUME 2Exercise:INTEGER_TYPE
Explore 10 Videos
- NEWTON'S LAWS OF MOTION 2Book:CENGAGE PHYSICS ENGLISHChapter:NEWTON'S LAWS OF MOTION 2Exercise:Integer type
Explore 1 Video
Similar Questions
Find the tension in the horizontal string PQ and the string QR in the given figure. [Take g=10m/s2]
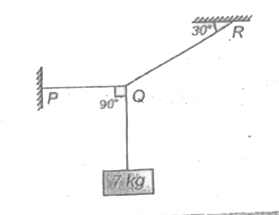
View SolutionFind the tension in the horizontal string PQ and the string QR in the given figure [ Take g =10m/s2]

View SolutionA body of weight 2 kg is suspended as shown in the figure. The tensionT1 in the horizontal string (in kg wt ) is
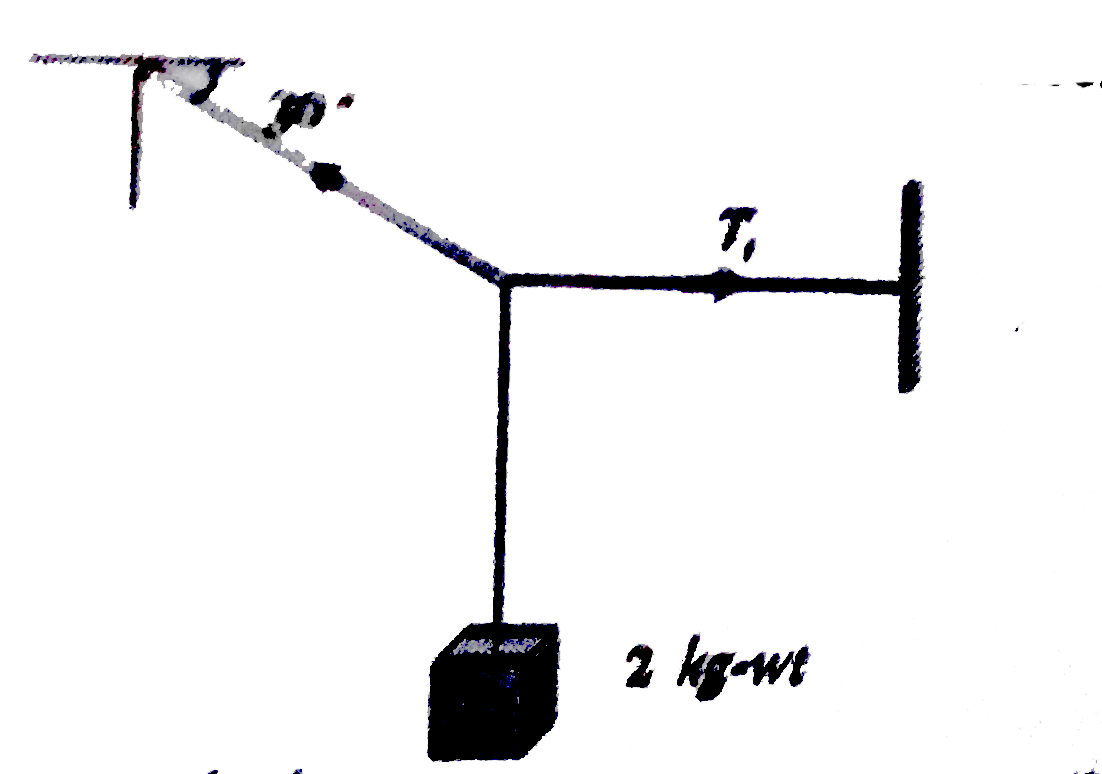
View SolutionA body of weight 2 kg is suspended as shown in the figure. The tension T2 in the horizontal string (in kg wt) is :-
View SolutionAn elevator weighing 6000 kg is pulled upward by a cable with an acceleration of 5ms−2 . Taking g to be 10ms−2 , then the tension in the cable is
View SolutionA lift of mass 200 kg is moving upward with an acceleration of 3m/s2 . If g=10m/s2 then the tension of string of the lift will be :
View SolutionA car is moving on a plane inclined at 30∘ to the horizontal with an acceleration of 10m/s2 parallel to the plane upward. A bob is suspended by a string from the roof. The angle in degrees which the string makes with the vertical is: (Assume that the bob does not move relative to car) [g=10m/s2]
View SolutionTwo bodies A (30 kg) and B (50 kg) tied with a light string are placed on a friction less table. A force F acting at B pulls this system with an acceleration of 2ms−2. The tension in the string is:
View SolutionThe normal reaction on a body placed in a lift moving up with constant acceleration 2ms−1 is 120 N. Mass of the body is (Take g=10ms−2)
View SolutionA block of mass 1kg is tied to a string of length 1m the other end of which is fixed The block is moved on a smooth horizontal table with constant speed 10ms−1. Find the tension in the string
View Solution