A plank is held at an angle α to the horizontal on two fixed supports A and B. The plank can slide against the supports (without friction) because of the weight Mg sinα. The acceleration and direction in which a man of mass m should move so that the plank does not move are

a. gsinα(1+mM) down the incline
b. gsinα(1+Mm) down the incline
c. gsinα(1+mM) up the incline
d. gsinα(1+Mm) up the incline
The correct Answer is:B
Free-body diagram of man and plank is given below.

For plank to be at rest, applying Newton's second law to plank along the incline
Mgsinα=f ..(i)
And applying Newton's second law to man along the incline,
mgsinα+f=ma...(ii)
⇒a=gsinα(1+Mm) down the incline.
Topper's Solved these Questions
- NEWTON'S LAWS OF MOTION 1BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - NEWTON'S LAWS OF MOTION 1EXERCISE - Multiple Correct
11 Videos
- NEWTON'S LAWS OF MOTION 1BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - NEWTON'S LAWS OF MOTION 1EXERCISE - Assertion-reasoning
15 Videos
- NEWTON'S LAWS OF MOTION 1BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - NEWTON'S LAWS OF MOTION 1EXERCISE - Subjective
15 Videos
- MISCELLANEOUS VOLUME 2BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - MISCELLANEOUS VOLUME 2EXERCISE - INTEGER_TYPE
10 Videos
- NEWTON'S LAWS OF MOTION 2BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - NEWTON'S LAWS OF MOTION 2EXERCISE - Integer type
1 Videos
Similar Questions
A solid uniform disc of mass m rolls without slipping down a fixed inclined plank with an acceleration a. The frictional force on the disc due to surface of the plane is
View SolutionA solid uniform disc of mass m rols without slipping down a fixed inclined plank with an acceleration a. The frictional force on the disc due to surface of the plane is
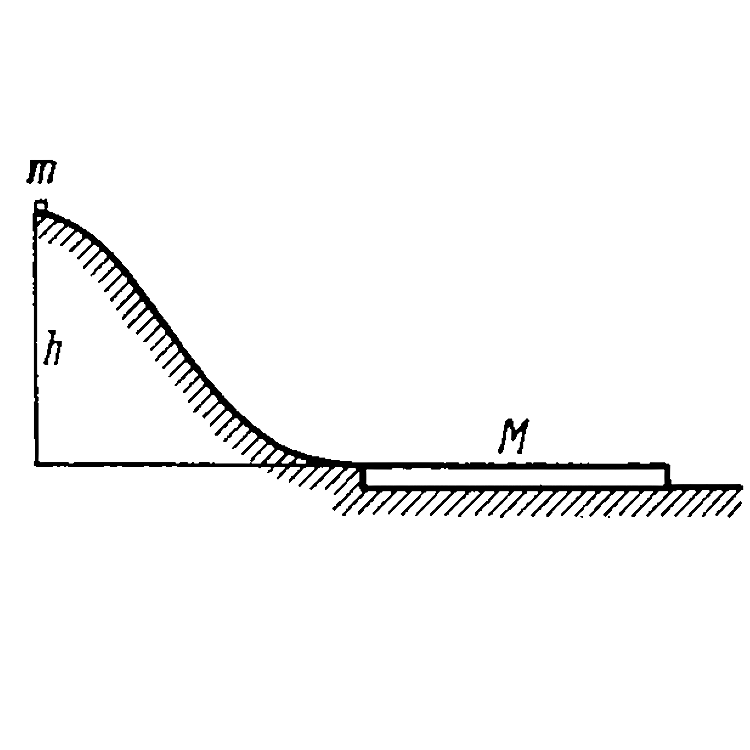
View SolutionA small disc of mass m slides down a smooth hill of height h without initial velocity and gets onto a plank of mass M lying on the horizontal plane at the base of the hill. (figure). Due to friction between the disc and the plank the disc slows down and, beginning with a certain moment, moves in one piece with the plank.
(1) Find the total work performed by the friction forces in this process.
(2) Can it be stated that the result of obtained does not depend on the choice of the reference frame?
View SolutionA block of mass 2 kg rests on an inclined plane which makes an angle of 30∘ with the horizontal. The coefficient of friction between the block and the surface is √3/2. (i) What force should be applied on the block so that it moves down without any acceleration ? (ii) What force should be applied on the block so that it moves up without any acceleration ? (iii) Calculate the ratio of the powers in the above two cases if the block moves with uniform speed in both the cases.
View SolutionA plank of mass M is placed on a rough horizontal surface and a contant horizontal force F is applied on it . A man of mass m runs on the plank find the range of acceleration of the man that the plank does not move on the surface is μ .Assume that the does not slip on the plank

View SolutionA plank A of mass M rests on a smooth horizontal surface over which it can move without friction A cabe B of mass m lies on the plank at one edge .The coefficient of friction between the plank and the cube is μ The size of cube is very small in comparison to the plank.

At what force F applied to the plank in the horizontal direction will be cube begin to slide towards the other end of the plank?
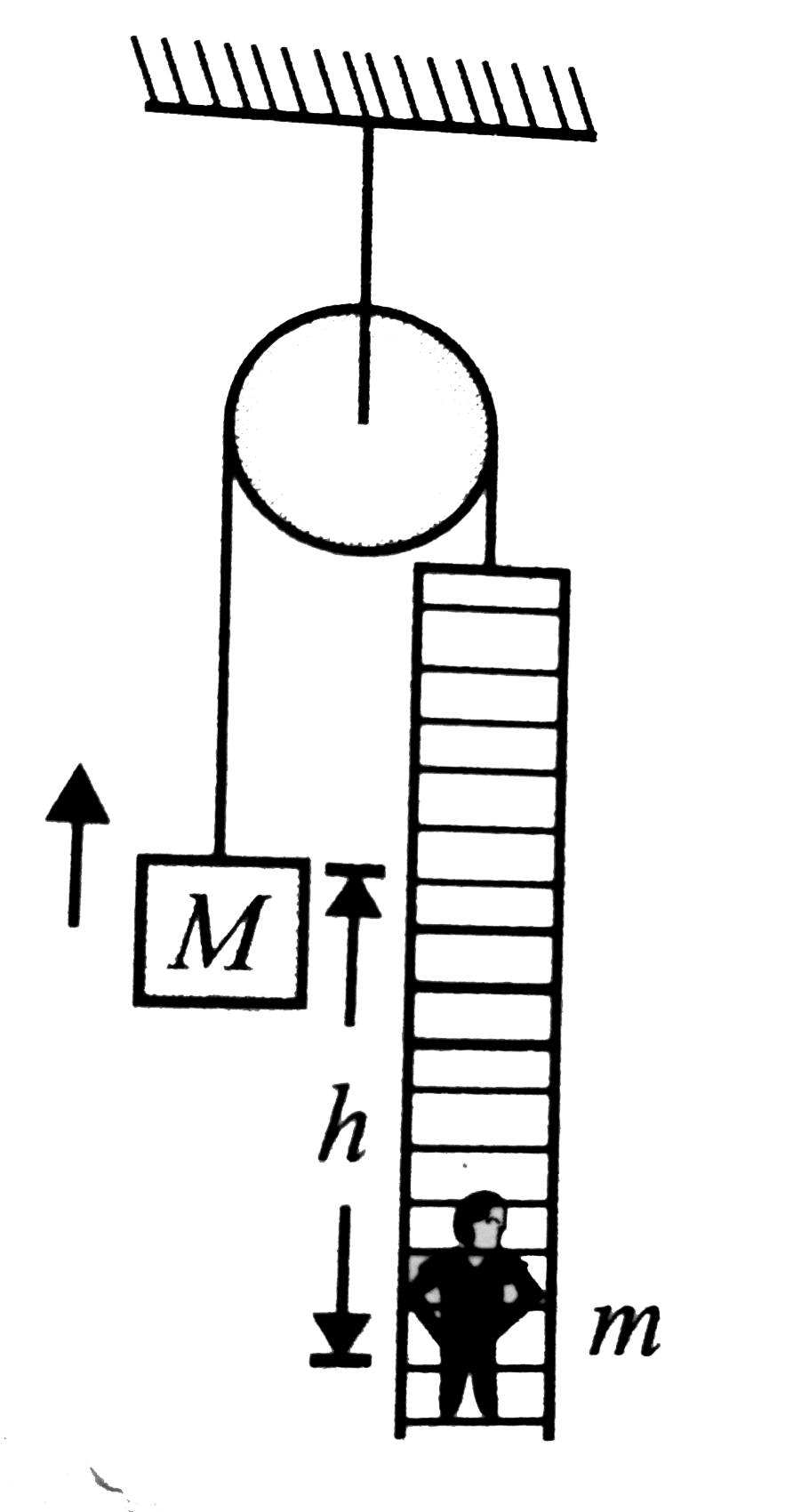
View SolutionA stationary light, smooth pulley can rotate without friction about a fixed horizontal axis. A light rope passes over the pulley. One end of the rope supports a ladder with man and the other end supports a counterweight of mass M. Mass of the man is m. initially, the centre of mass of the counterweight is at a height h from that of man as shown in Fig.
If the man starts to climb up the ladder slowly, calculate work done by him to reach his centre of mass in level with that of the counterweight.
View SolutionA plank of mass M is placed on a rough horizontal surface. A man m walks on the plank with an acceleration 'a' while the plank is also acted upon by a horizontal force F whose magnitude and direction can be adjusted to keep the plank at rest.
The coefficient of friction between plank and surface is μ. Choose the correct options.
 .
.
View SolutionA plank of mass m rests symmetrically on two wedges B and C of mass M. What is the acceleration of the plank? Neglect friction between all the contact surfaces.

View SolutionA uniform disc of mass M and radius R initially stands vertically on the right end of a horizontal plank of mass M and length L, as shown,
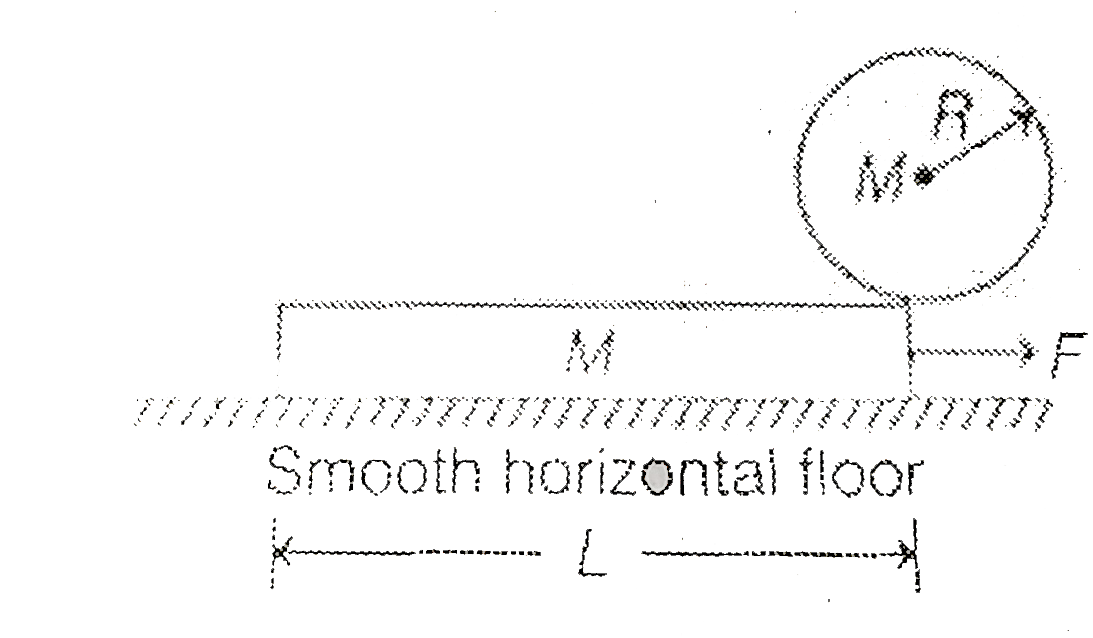
The plank rests on a smooth horizontal floor and friction between disc and plank is sufficiently high such that disc rolls on plank without slipping . The plank is pulled to right with a constant horizontal force of magnitude F.
The magnitude of acceleration of plank is
F/ 6 M
F/ 4 M
3 F/ 2 M
3 F/ 4 M
View Solution
