An inextensible string AB is tied to a block B of negligible dimensions and passes over a small pulley C so that free end A hangs h unit above the ground on which the block B rests. In this initial position shown in fig. The free end A is h unit below C. if now end A moves horizontally with a velocity , obtain an expression for the velocity of the block at any time t.

In time t, the end A moves to the position so that distance . The block B moves upwards to the position . Let .
Then length
In the
or
or
After solving eq. (i) we get
This is the equation for the displacement y of the block.
For velocity of the block differentiating equation (i) w.r.t. time
.

Topper's Solved these Questions
- NEWTON'S LAWS OF MOTION 1BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - NEWTON'S LAWS OF MOTION 1EXERCISE - Exercise 6.4
13 Videos
- NEWTON'S LAWS OF MOTION 1BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - NEWTON'S LAWS OF MOTION 1EXERCISE - Subjective
15 Videos
- NEWTON'S LAWS OF MOTION 1BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - NEWTON'S LAWS OF MOTION 1EXERCISE - Exercise 6.2
35 Videos
- MISCELLANEOUS VOLUME 2BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - MISCELLANEOUS VOLUME 2EXERCISE - INTEGER_TYPE
10 Videos
- NEWTON'S LAWS OF MOTION 2BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - NEWTON'S LAWS OF MOTION 2EXERCISE - Integer type
1 Videos
Similar Questions
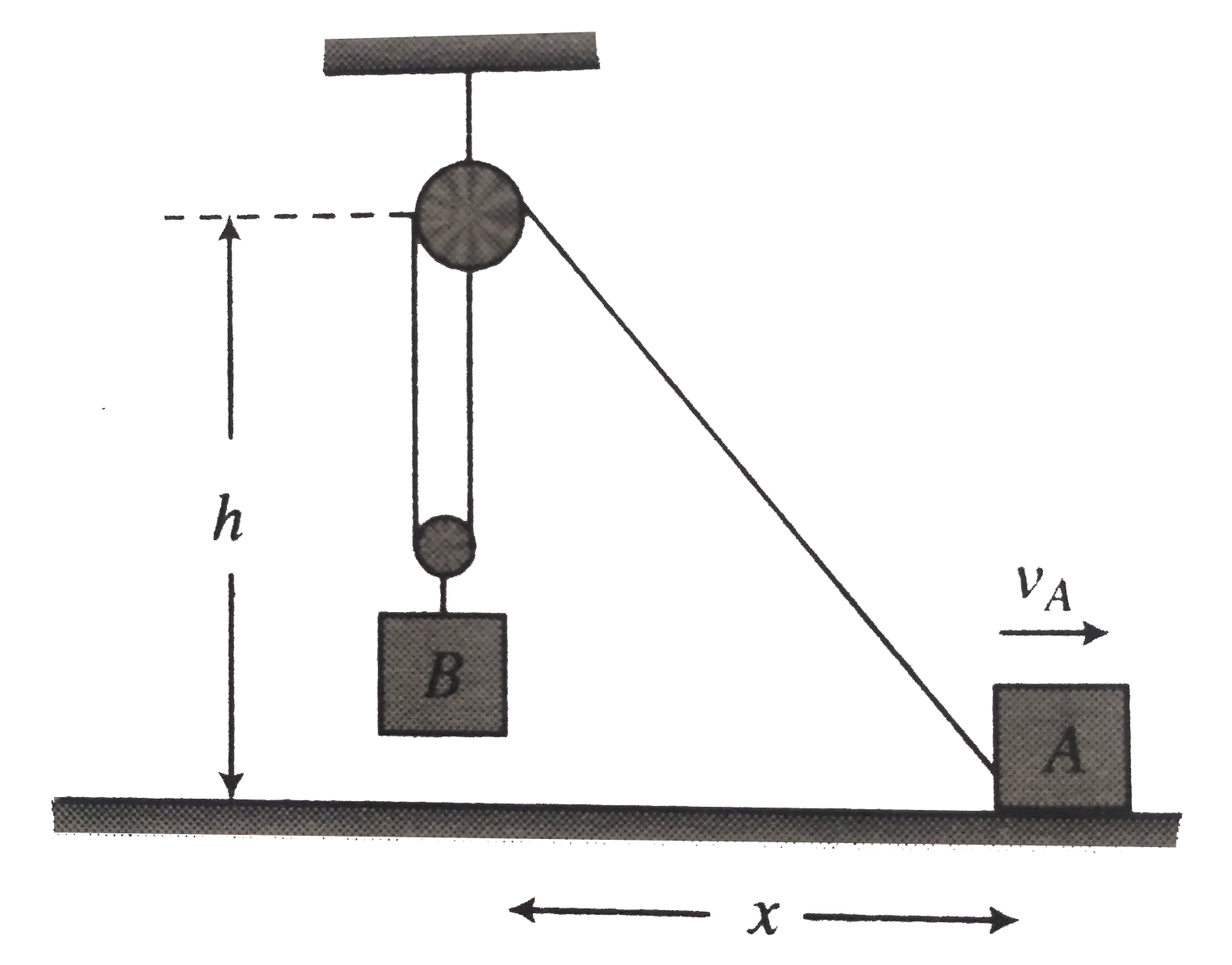
If block A is moving horizontally with velocity vA, then find the velocity of block B at the instant as shown in fig.
View SolutionA block is dragged on a smooth plane with the help of a rope which moves with a velocity v as shown in figure. The horizontal velocity of the block is :

View SolutionIn the system shown, the block A is moving down eith velocity v1 and C is moving up with velocity v3. Express velocity of the block B in terms of velocities of the blocks a and C.

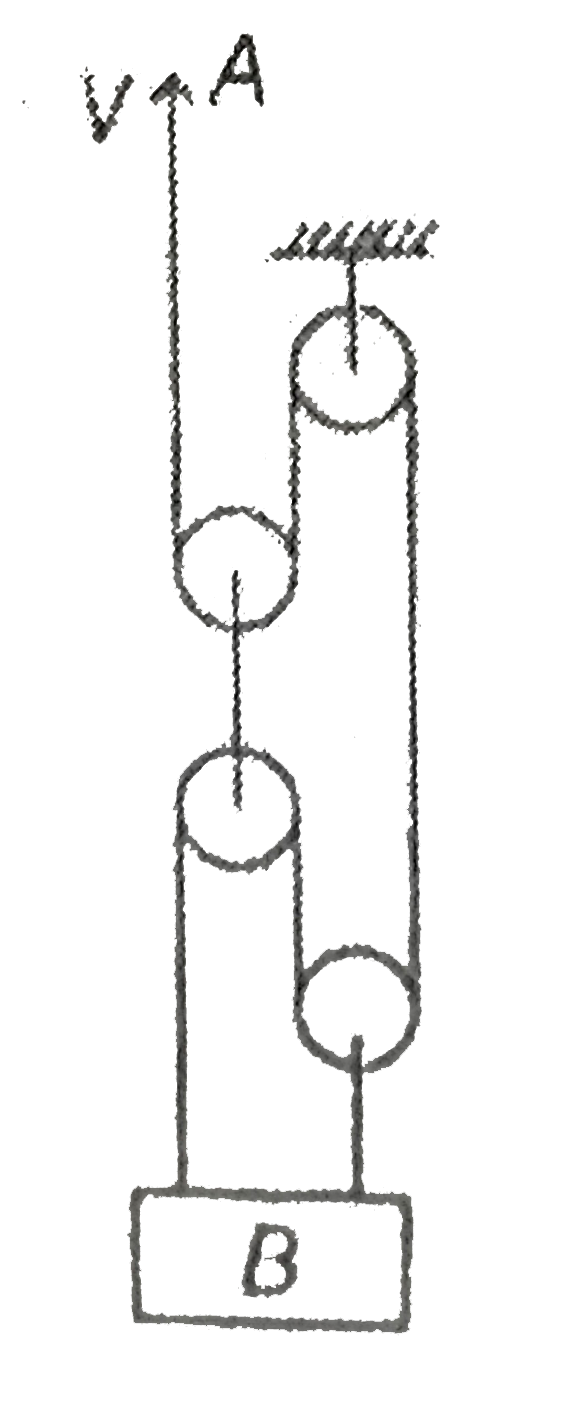
View SolutionIn the arrangement shown, end A of light intextensible string is pulled with constant velocity v. the velocity of block B is
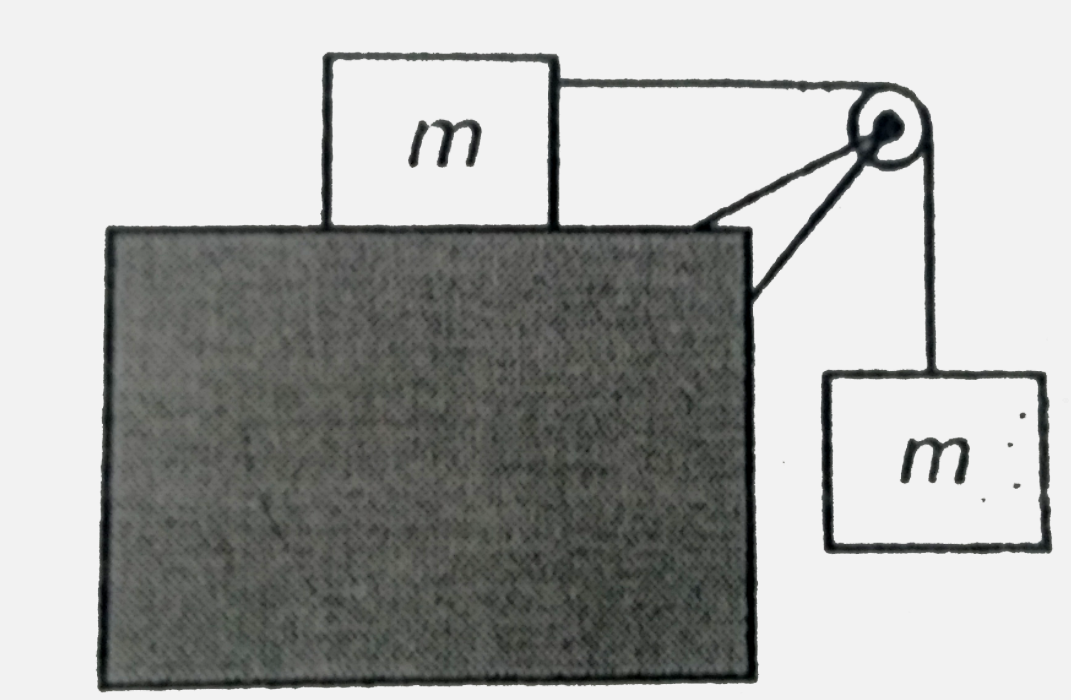
View SolutionTwo identical masses are attached by a light string that passes over a small pulley, as shown . The table and the pulley are frictionless. The hanging block is moving
View SolutionThe block A is moving downward with constant velocity v0. Find the velocity of the block B. When the string makes an angle θ with the horizontal

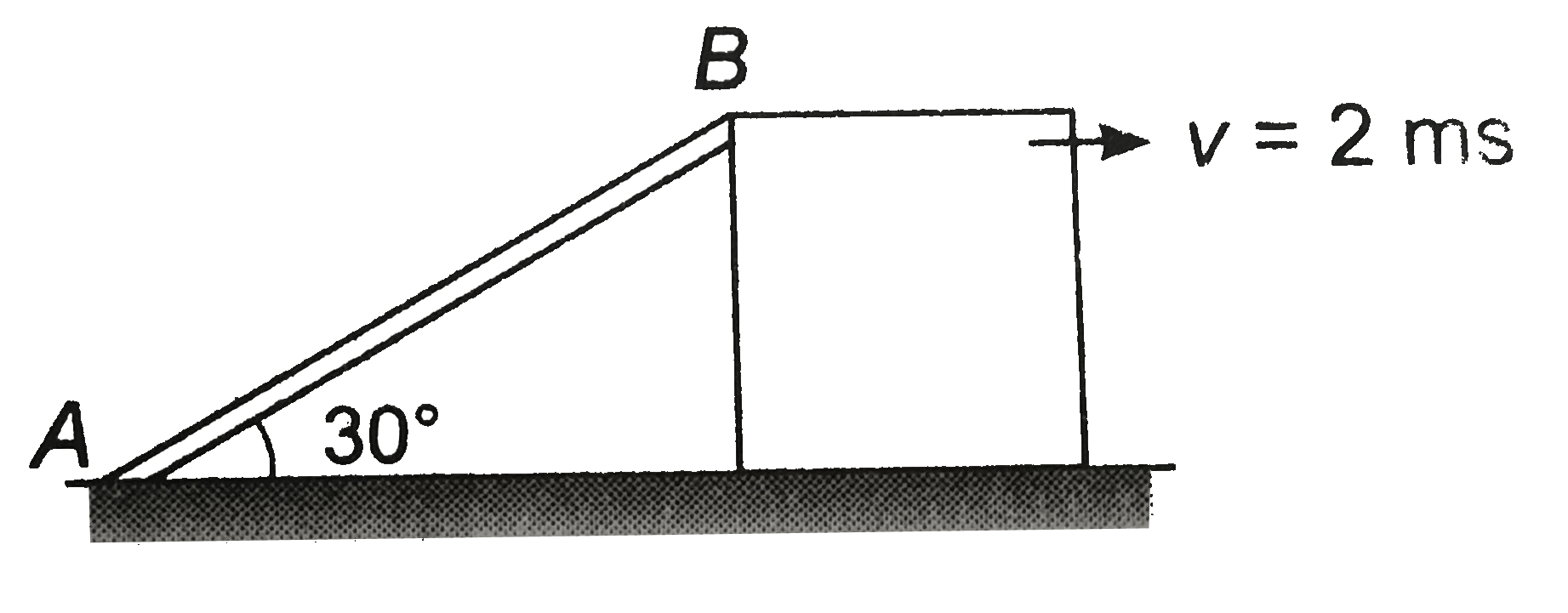
View SolutionA rod AB is shown in figure. End A of the rod is fixed on the ground. Block is moving with velocity 2ms−1 towards right. The velocity of end B of rod at the instant shown in figure is
View SolutionWhen a stick is released (as shown in fig.). Its free end velocity when it strikes the ground is

View SolutionA block of mass m is tied to a string of length L and the assembly is kept on a smooth horizontal table as shown in the figure. Now the other end of the string is moved with a constant velocity v0ˆj. (xy plane is the plane of the table) Then

View SolutionA string of negligible mass passes over a pulley of mass m which is clamped. It supports a block of mass M at its lower free end. What is force exerted on pulley by the support ?
View Solution
