A ring A which can slide on a smooth wire is connected to one end of a string as shown in fig. Other end of the string is connected to a hanging mass B. Find the speed of the ring when the string makes an angle θ with the wire and mass B is going down with a velocity v.
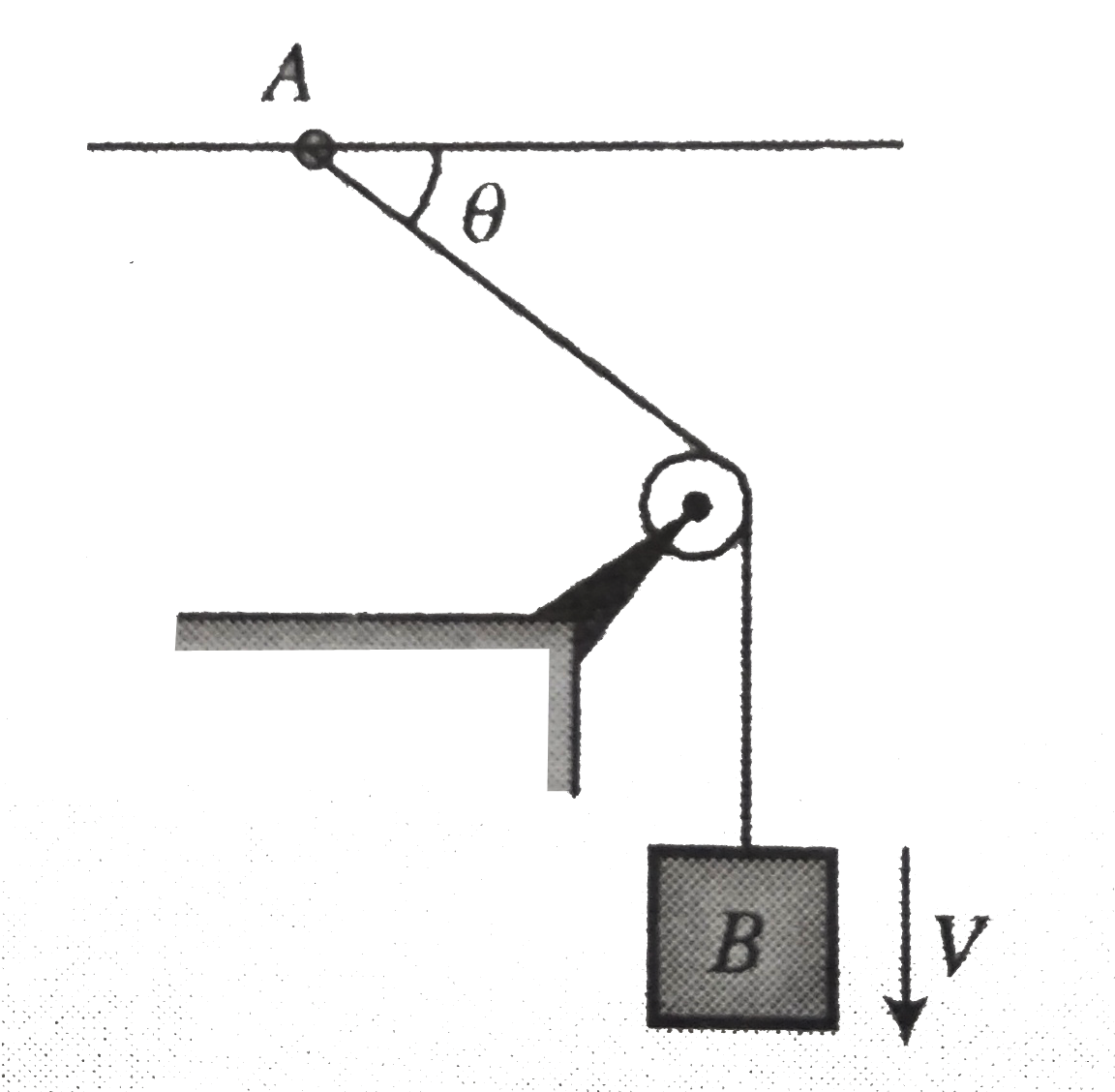
Let the speed of the ring is u, then ucosθ=v.Because components of velocity along the string should be same.
⇒u=v/cosθ=vsecθ.

Topper's Solved these Questions
- NEWTON'S LAWS OF MOTION 1BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - NEWTON'S LAWS OF MOTION 1EXERCISE - Exercise 6.4
13 Videos
- NEWTON'S LAWS OF MOTION 1BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - NEWTON'S LAWS OF MOTION 1EXERCISE - Subjective
15 Videos
- NEWTON'S LAWS OF MOTION 1BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - NEWTON'S LAWS OF MOTION 1EXERCISE - Exercise 6.2
35 Videos
- MISCELLANEOUS VOLUME 2BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - MISCELLANEOUS VOLUME 2EXERCISE - INTEGER_TYPE
10 Videos
- NEWTON'S LAWS OF MOTION 2BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - NEWTON'S LAWS OF MOTION 2EXERCISE - Integer type
1 Videos
Similar Questions
The block A is moving downward with constant velocity v0. Find the velocity of the block B. When the string makes an angle θ with the horizontal

View Solution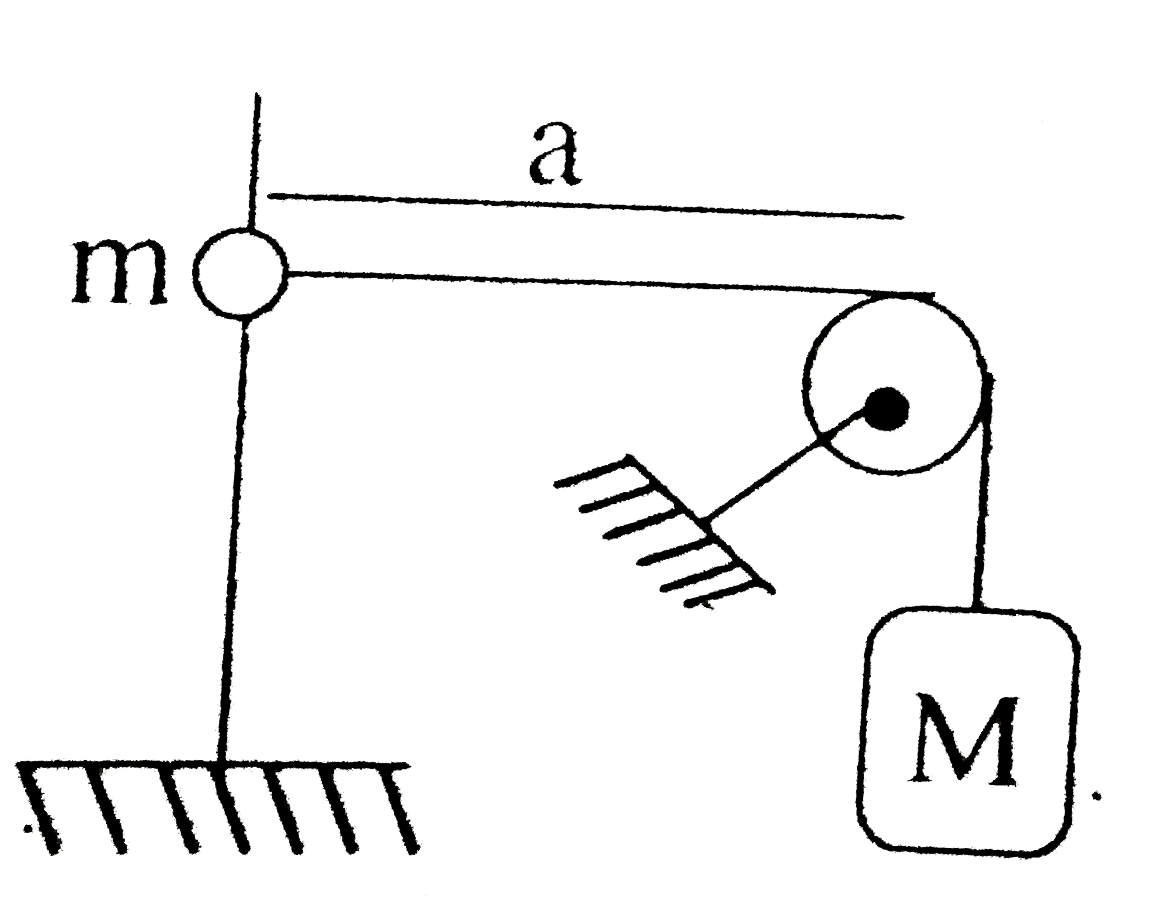
A ring of mass m can slide on the vertical smooth rod. Ring is connected by block with string as shown in figure. Pulley is of mass-less and smooth the system is released from reast. Initial tension in string is
View SolutionA particle is rotated in a vertical circle by connecting it to a string of length l and keeping the other end of the string fixed. The minimum speed of the particle when the string is horizontal for which the particle will complete the circle is
View SolutionA bead can slide on a smooth straight wire and a particle of mass m attached to the bead by a light string of length L. The particle is held in contact with the wire and with the string taut and is then let fall. If the bead has mass 2m then when the string makes an angle θ with the wire, the bead will have slipped a distance.

View SolutionA block of mass m can slide freely in a slot made in a bigger of mass M as shown in fig. There is no friction anywhere in the system.

The block m is connected to one end of a string whose other end is fixed at point P. system is released from rest when the string at P makes an angle θ with horizontal. Find the acceleration of m and M after release.
View SolutionA stone of mass m tied to a string of length l is rotated in a circle with the other end of the string as the centre. The speed of the stone is v. If the string breaks, the stone will move
View SolutionA simple pendulum is constructed by attaching a bob of mass m to a string of length L fixed at its upper end. The bob oscillates in a vertical circle. It is found that the speed of the bob is v when the string makes an angle θ with the vertical. Find the tension in the string at this instant.
View SolutionA disk is fixed at its centre O and rotating with constant angular velocity ω. There is a rod whose one end is connected at A on the disc and the other end is connected with a ring which can freely moce along the fixed vertical smooth rod. At an instant when the rod is making an angle 30∘ with the vertical the ring is found to have a velocity v in the upward direction. Find ω of the disk. Given that the point A is R/2 distance above point O and length of the rod Ab is l
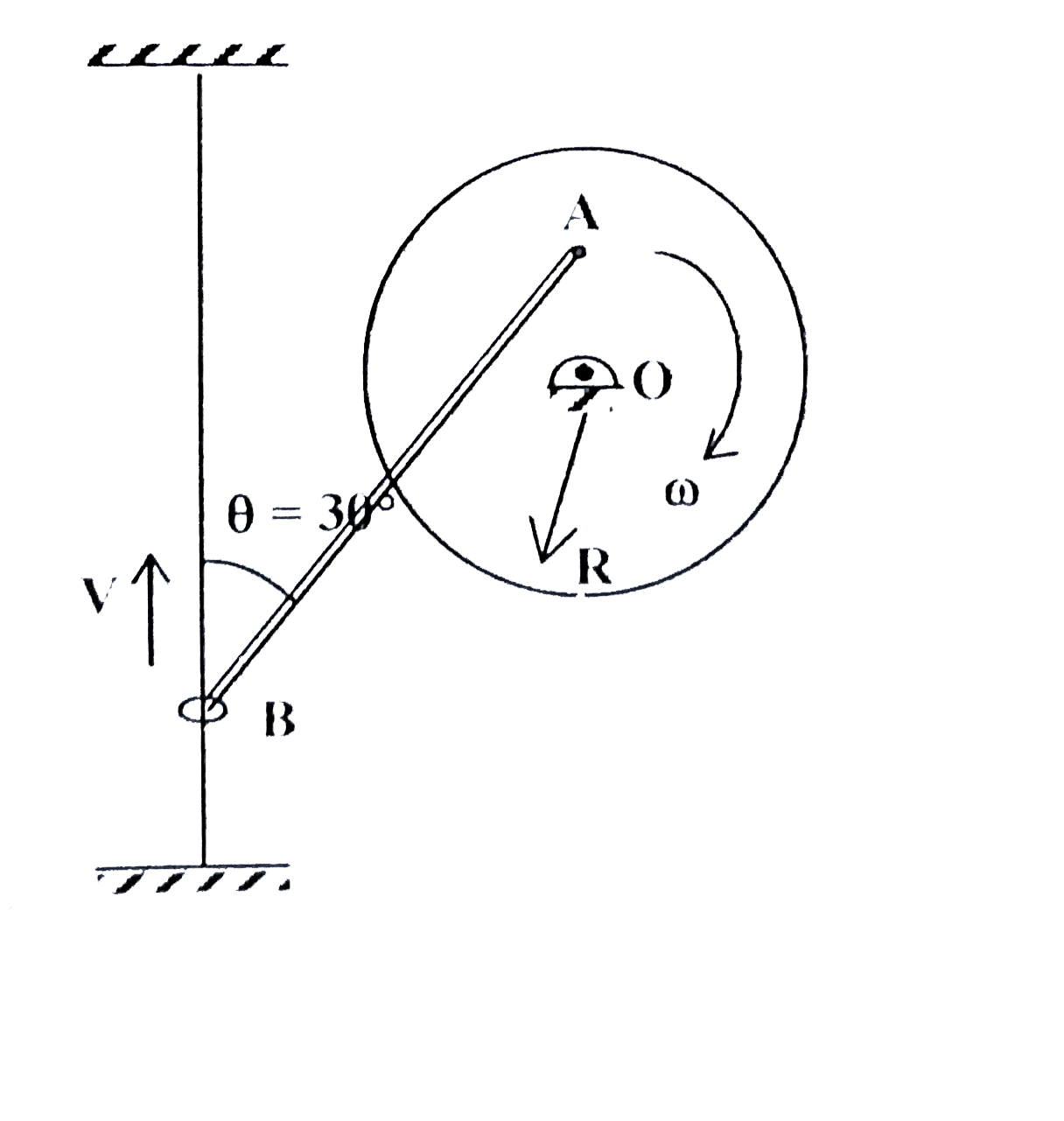
View SolutionA sphere of mass M is held at rest on a horizontal floor. One end of a light string is fixed at a point that is vertically above the centre of the sphere. The other end of the string is connected to a small particle of mass m that rest one the sphere. The string makes an angle α=30∘ with the vertical. Then the acceleration of the spherer immediately after it is released is : (There is no frication anywhere and string is tangene to the sphere) :

View SolutionA system of men and trolley is shown in Fig. To the left, end of the string, a trolley of mass M is connected on which a man of mass m is standing. To the right end of the string another trolley of mass m is connected on which a man of mass M is standing. Initially, the system is at rest. All of a sudden both the men leap upwards simultaneously with the same velocity u w.r.t. ground.

Find the impulse generated in the string connecting the trolleys during this process.
View Solution
