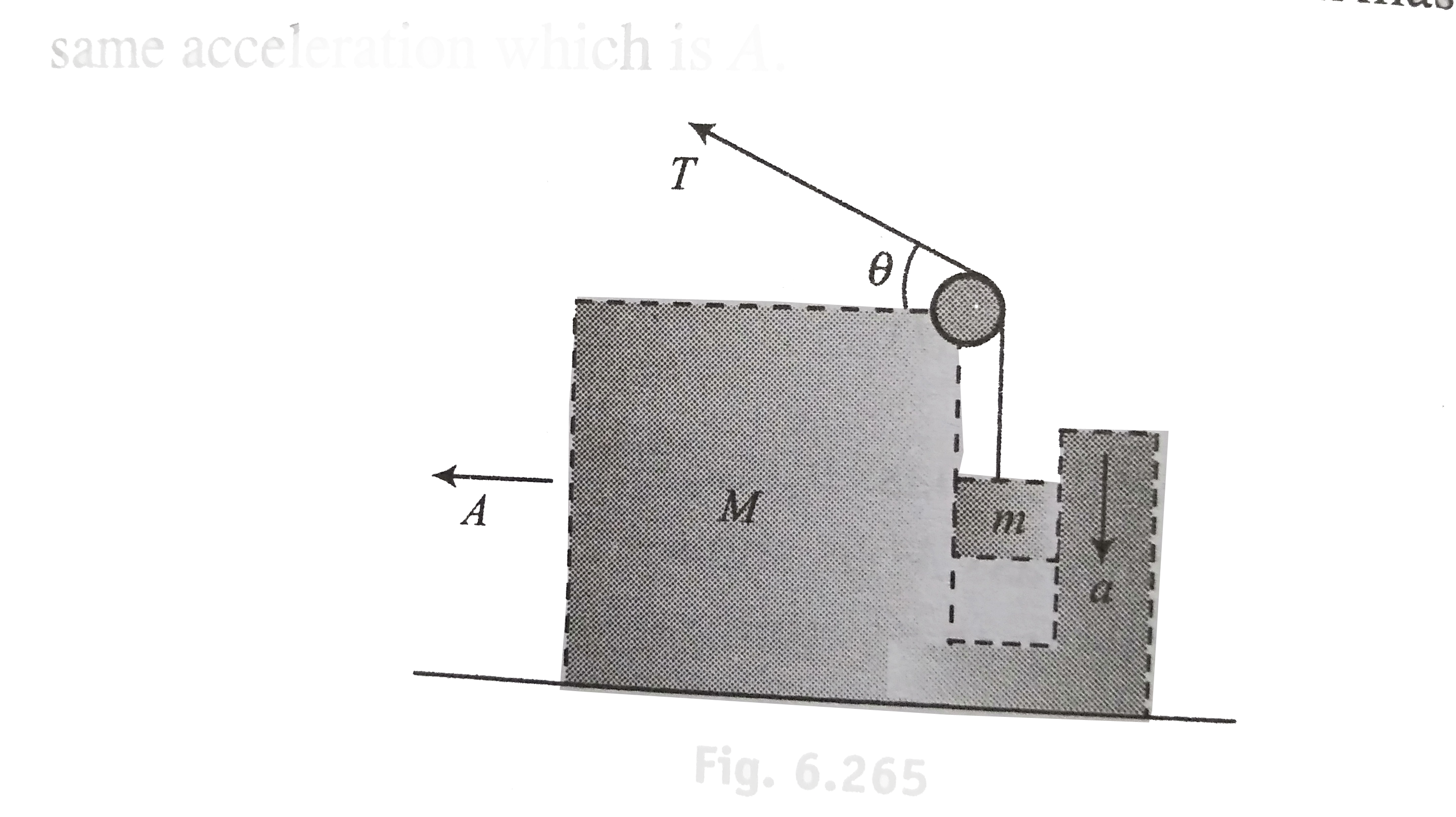
A block of mass m can slide freely in a slot made in a bigger of mass M as shown in fig. There is no friction anywhere in the system.

The block m is connected to one end of a string whose other end is fixed at point P. system is released from rest when the string at P makes an angle θ with horizontal. Find the acceleration of m and M after release.
Method 1: Just after the release of system, block M will move towards left (say with acceleration A) and block m will move down with respect ot M (say with acceleration a). As there is no motion of M is vertical direction, hence the acceleration of m in verticle direction will be same as that of M, i.e. A, because horizontal both move together.
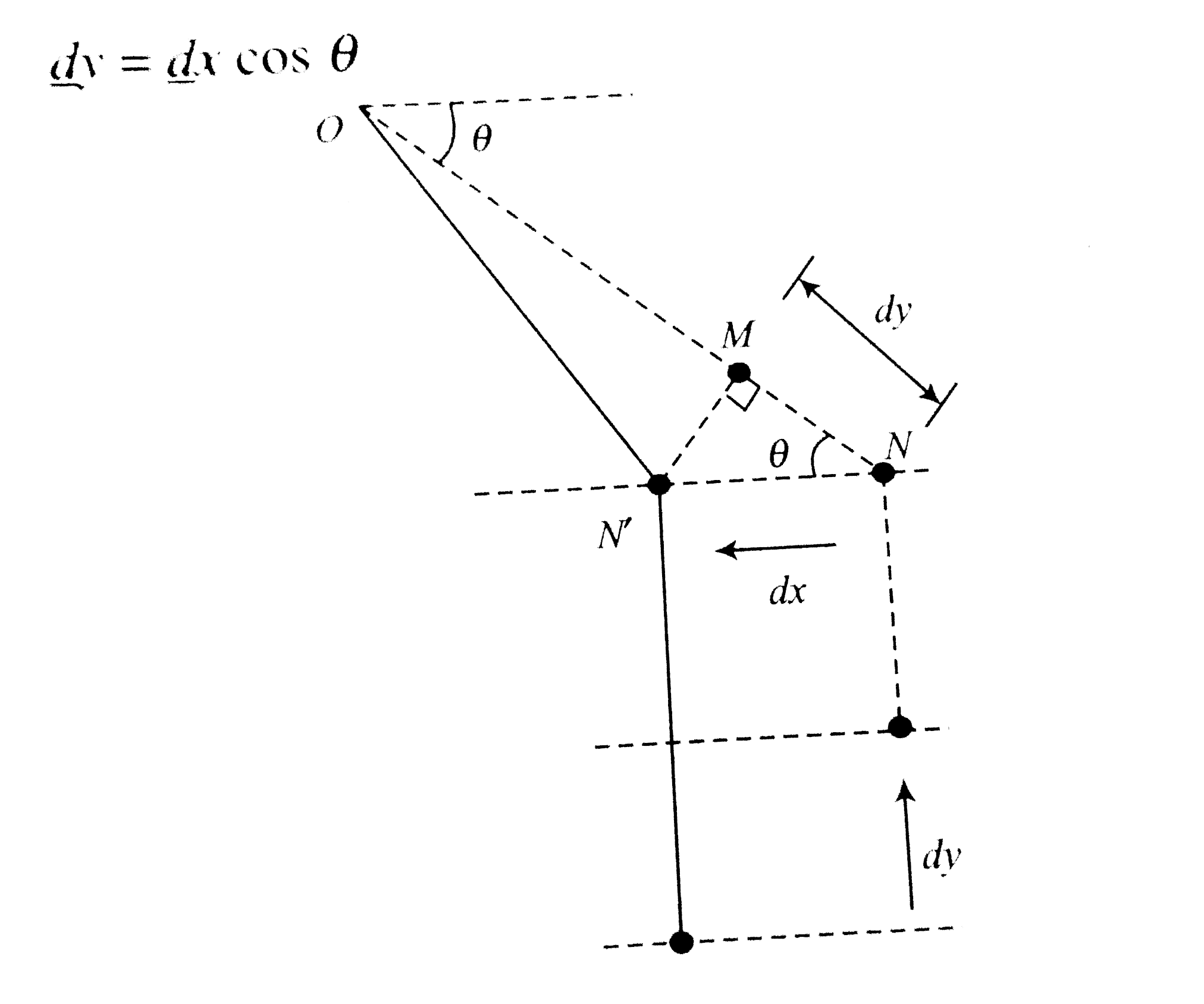
Finding constraint Method 1: Let just after release, during a small time dt, the displacement of m(w.r.t. M) is dy downwards and that of M is dx horizontally as shown in fig.
Decreases in the length of segment I=d¯xcosθ
Increases in the length of segment II' d¯y
As the total length of the string is constant , so
d¯=d¯xcosθ ..(i)
Divinding both sides by dt, we get
dydt=dxdtcosθ⇒v=Vcosθ ..(ii)
differenting w.r.t. t=dvdt=V(−sinθ)dθdt+dVdtcosθ
But initially V=0, as a=Acosθ ...(iii)
(∴dvdt=a,dVdt=A)
Method 2: we can obtain (i) in the following way.
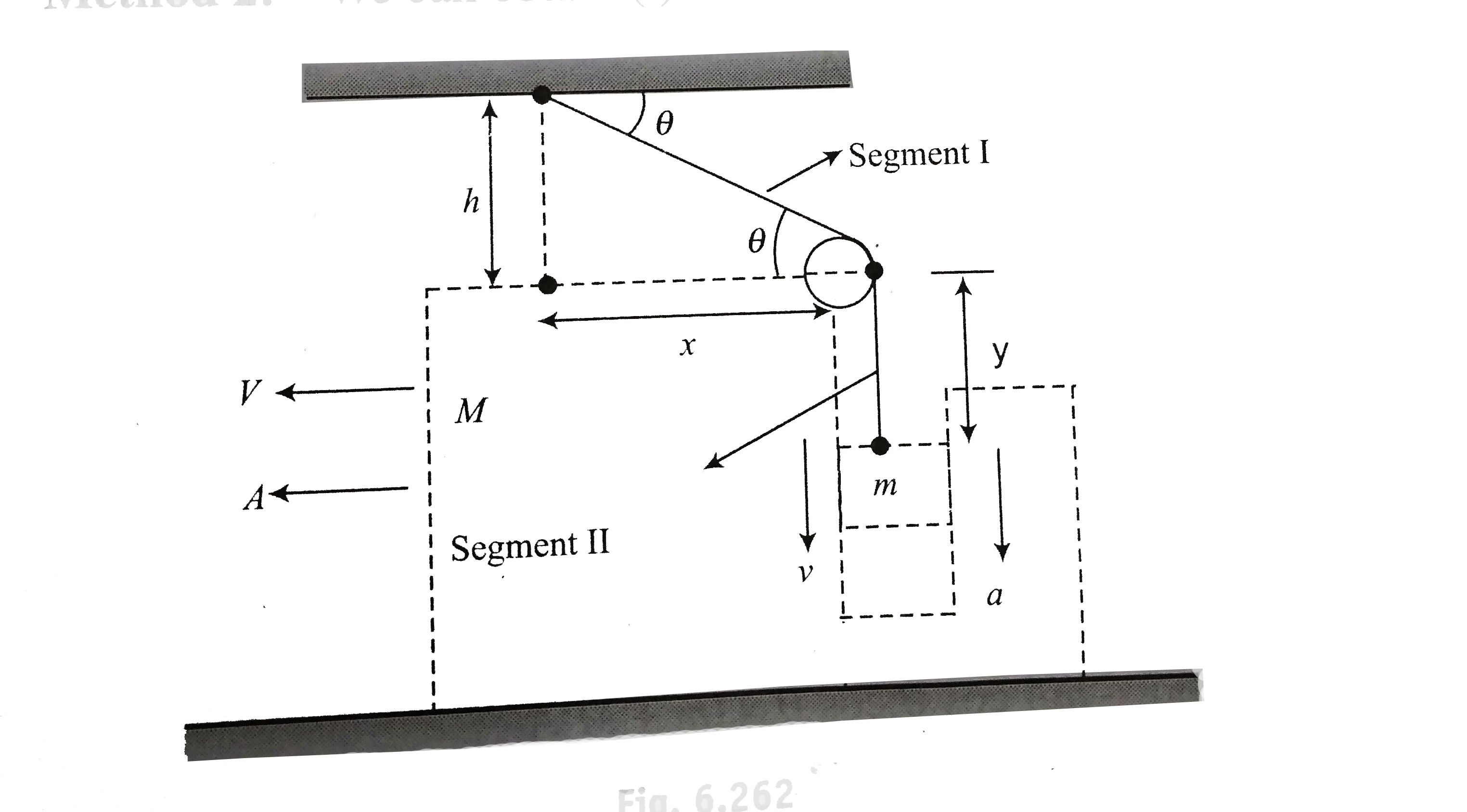
The displacment of M towards left is dx, then its component along AP is dxcosθ should be decreased in the length of segment I and this should be equal to increases in the length of segment II which is dy. Hence, dy=dxcosθ.
⇒a=Acosθ
Method 3:
Total length of string : l=√h2+y2+x
differentiating w.r.t. t=dldt=d(h2+x2)1/2dt+dxdt
⇒0=2ydydt2√h2+y2+dxdt⇒0=cosθ(−V)+r
(∵dxdt=v,dydt=−V (as y decreases with time)
and cosθ=y√h2+y2
⇒v=Vcosθ which is same as (ii)
Now finding acceleration of blocks
We can use any of the following method to find the value of A and a .

Method 1: From FBD of M:
Tcosθ−N=MA ...(iv)
From FBD of m: N=mA ..(v)
mg−t=ma ..(vi)
Combining (iv) and (v) we get
Tcosθ=(m+M)A ...(vii)
Putting a=Acosθ in (iv) we get
mg−T=mAcosθ ..(viii)
Put the value of T form (viii) into (vii) we get
(mg−mAcosθ)cosθ=(m+M)A
⇒A=mgcosθM+m(1+cos2θ)
and a=Acosθ=mgcos2θM+m(1+cos2θ)
The net acceleration of m is
√A2+a2=A√1+cos2θ=mgcosθ√1+cos2θM+m(1+cos2θ)
Method 2: Analyzing the block with w.r.t. wedge

W.r.t M, m has only vertcal acceleration which is a downwards. Here we have to apply pseudo force because M is a non inertial frame.
FBD of m w.r.t. M:
N=mA,mg−T=ma
These equation are same as (v) and (vi). Now solve to get answer.
Method 3: Analyzing the block and wedge together
Analyzing the system of (M+m), i.e. , block and wedge together in horizontal direction, in horizontal direction both masses have same acceleration which is A.
Tcosθ=(M+m)A ...(ix)
Analyzing the motion of blcok in vertical direction
mg−T=ma ..(x)

Solving (ix) and (x) , we get
A=mgcosθM+m(1+cos2θ)
and a=mgcos2θM+m(1+cos2θ)
Topper's Solved these Questions
- NEWTON'S LAWS OF MOTION 1BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - NEWTON'S LAWS OF MOTION 1EXERCISE - Exercise 6.1
11 Videos
- NEWTON'S LAWS OF MOTION 1BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - NEWTON'S LAWS OF MOTION 1EXERCISE - Exercise 6.2
35 Videos
- NEWTON'S LAWS OF MOTION 1BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - NEWTON'S LAWS OF MOTION 1EXERCISE - Integer
5 Videos
- MISCELLANEOUS VOLUME 2BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - MISCELLANEOUS VOLUME 2EXERCISE - INTEGER_TYPE
10 Videos
- NEWTON'S LAWS OF MOTION 2BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - NEWTON'S LAWS OF MOTION 2EXERCISE - Integer type
1 Video
Similar Questions
A block of mass m can slide freely along the verticle surface of a bigger block of mass M as shown in fig. There is no friction anywhere in the system. The block m is connected to one end is fixed at point P.
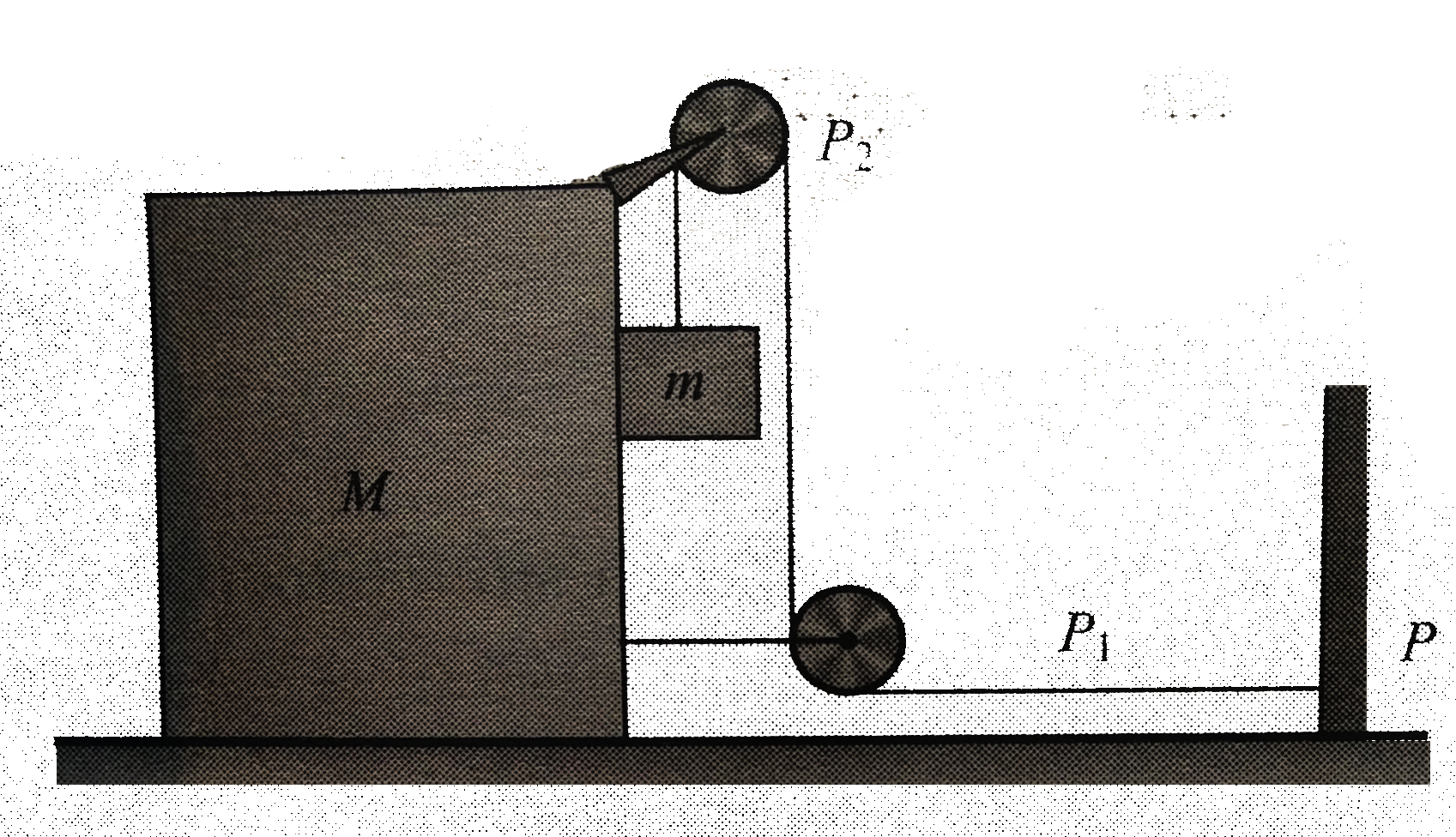
The string between P1 and P is horizontal and other parts of the string are vertical. system is released from rest. Find the acceleration of m and M during their subsequent motion.
View SolutionA block of mass m is released from a wedge of mass m as shown in figure . Find the time taken by the block to reach the end of the wedge.
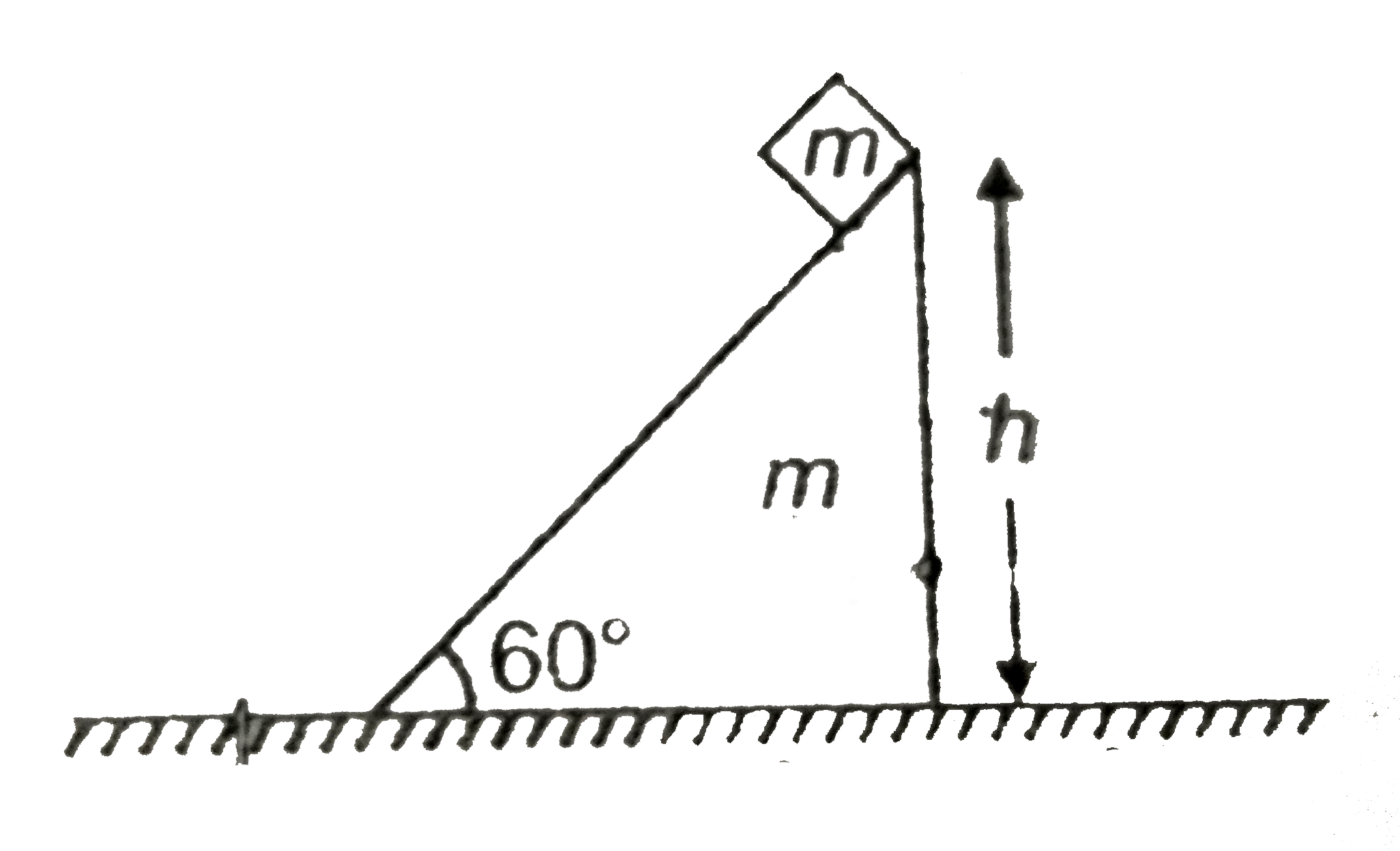
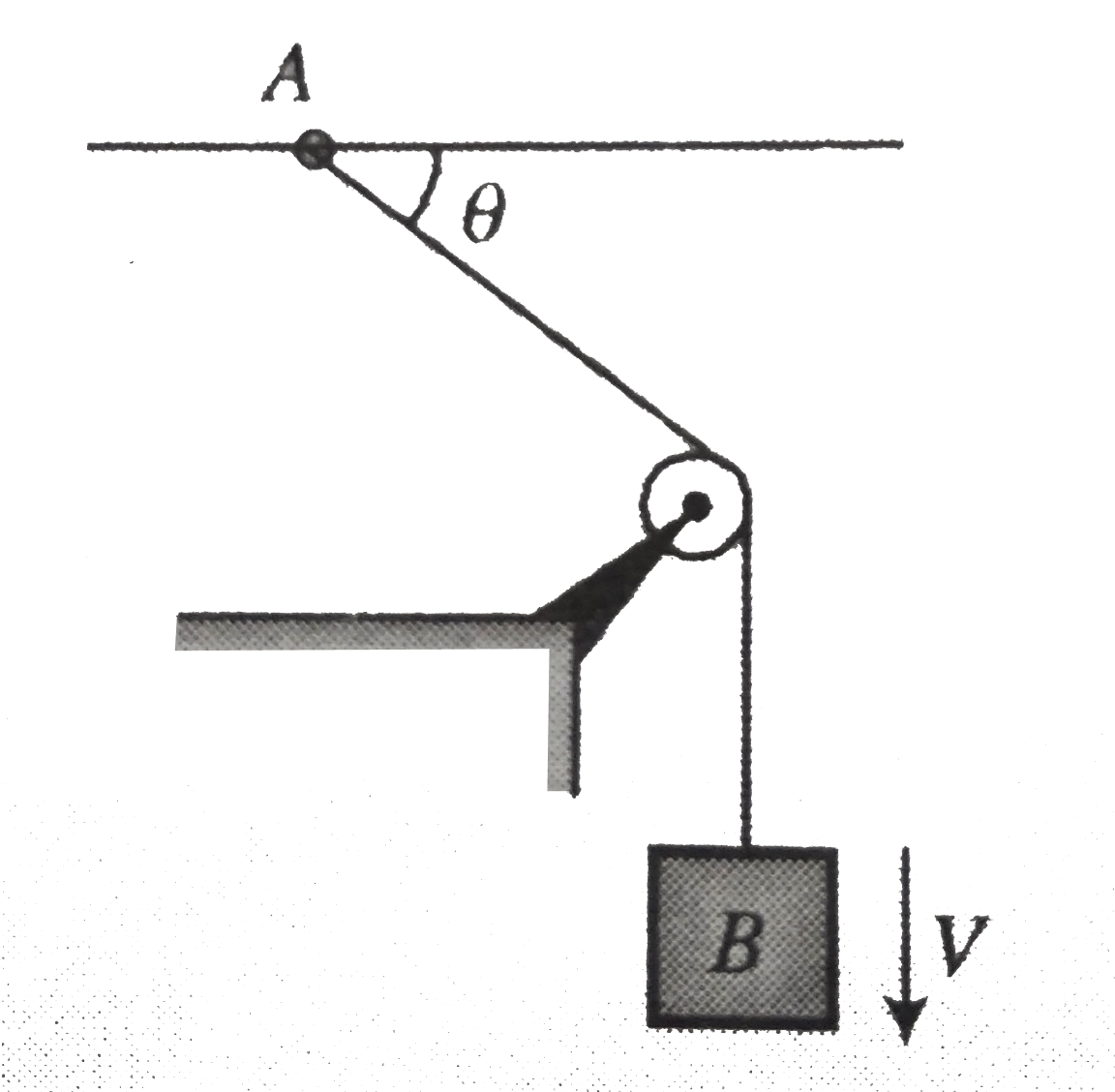
View SolutionA ring A which can slide on a smooth wire is connected to one end of a string as shown in fig. Other end of the string is connected to a hanging mass B. Find the speed of the ring when the string makes an angle θ with the wire and mass B is going down with a velocity v.
View SolutionA block of mass m is placed at rest on a smooth wedge of mass M placed at rest on a smooth horizontal surface. As the system is released

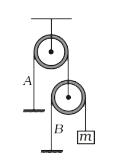
View SolutionThe block of mass m is at rest. Find the tension in the string A .
View SolutionA block of mass m is attached at the end of an inextensible string which is wound over a rough pulley of mass M and radius R figure a. Assume the string does not slide over the pulley. Find the acceleration of the block when released.
View Solution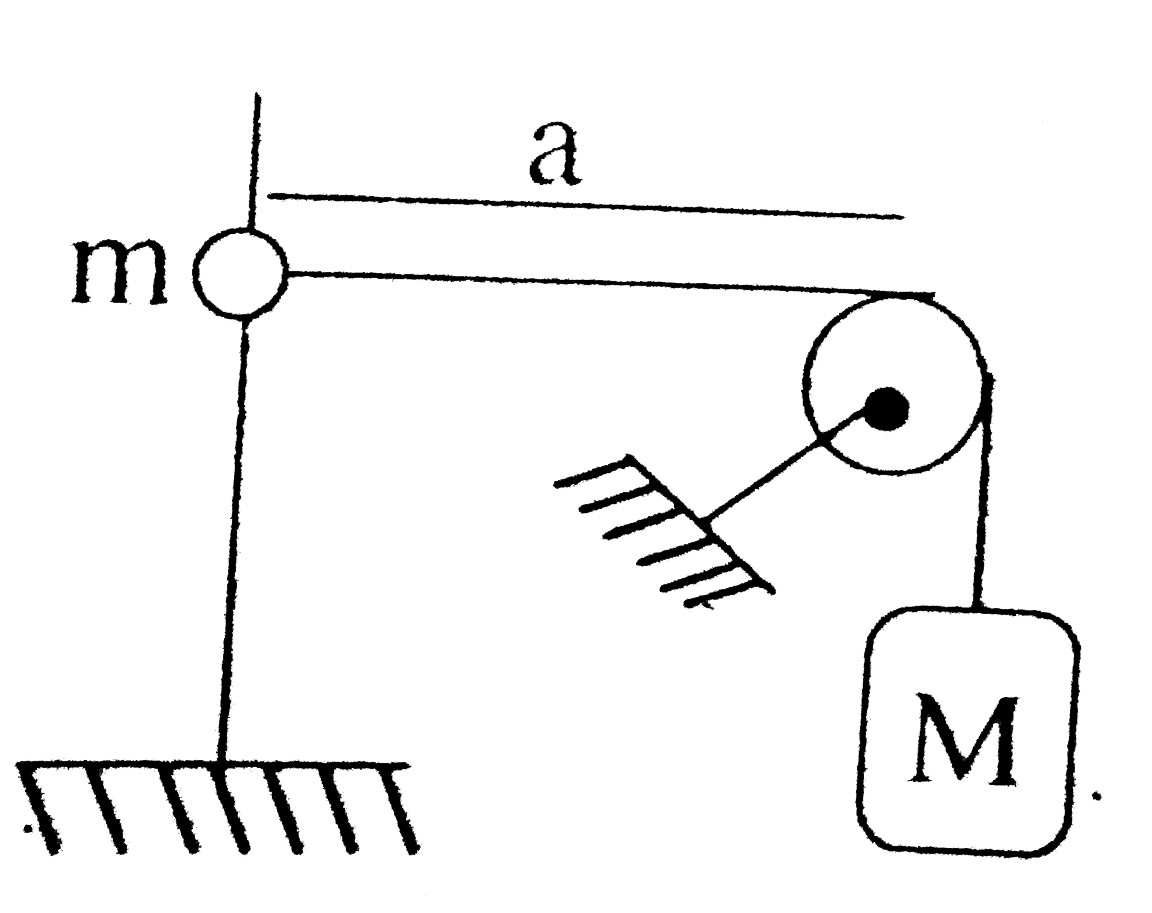
A ring of mass m can slide on the vertical smooth rod. Ring is connected by block with string as shown in figure. Pulley is of mass-less and smooth the system is released from reast. Initial tension in string is
View SolutionA block of mass M is placed on the top of a bigger block of mass 10 M as shown in figure. All the surfaces are frictionless. The system is released from rest, then the distance moved by the bigger block at the instant the smaller block reaches the ground :
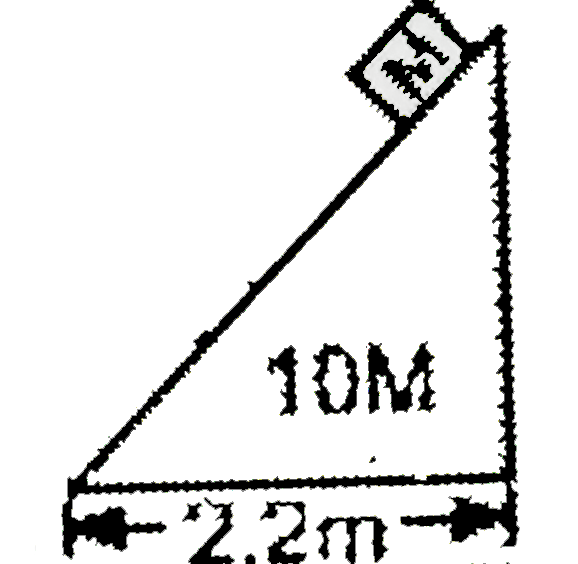
View SolutionIn the given figure, Find mass of the block A, if it remains at rest, when the system is released from rest. Pulleys and strings are massless. [g=10m/s2]

View SolutionA disc of mass m and radius r is free to rotate about its centre as shown in the figure. A string is wrapped over its rim and a block of mass m is attached to the free end of the string. The system is released from rest. The speed of the block as it descends through a height h, is :-
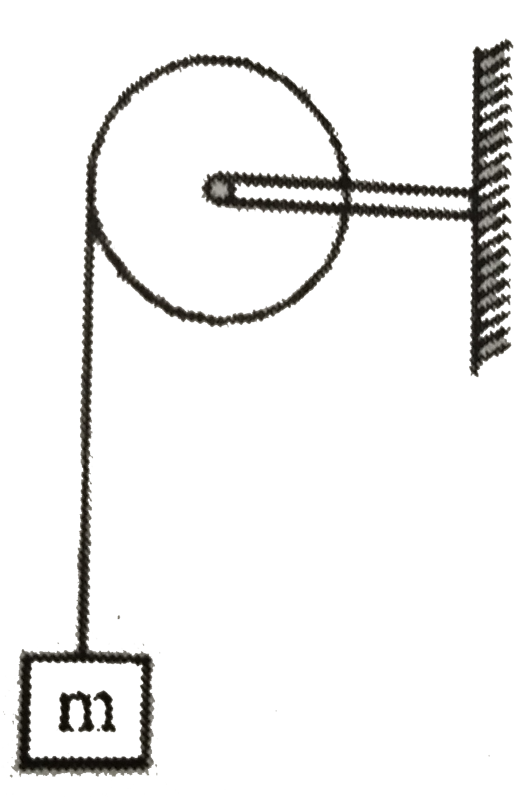
View Solution