The mass of wedge, shown in figure is M and that of the block is m. Neglecting friction at all the places and mass of the pulley. Calculate the acceleration of wedge. Thread is inextensible.

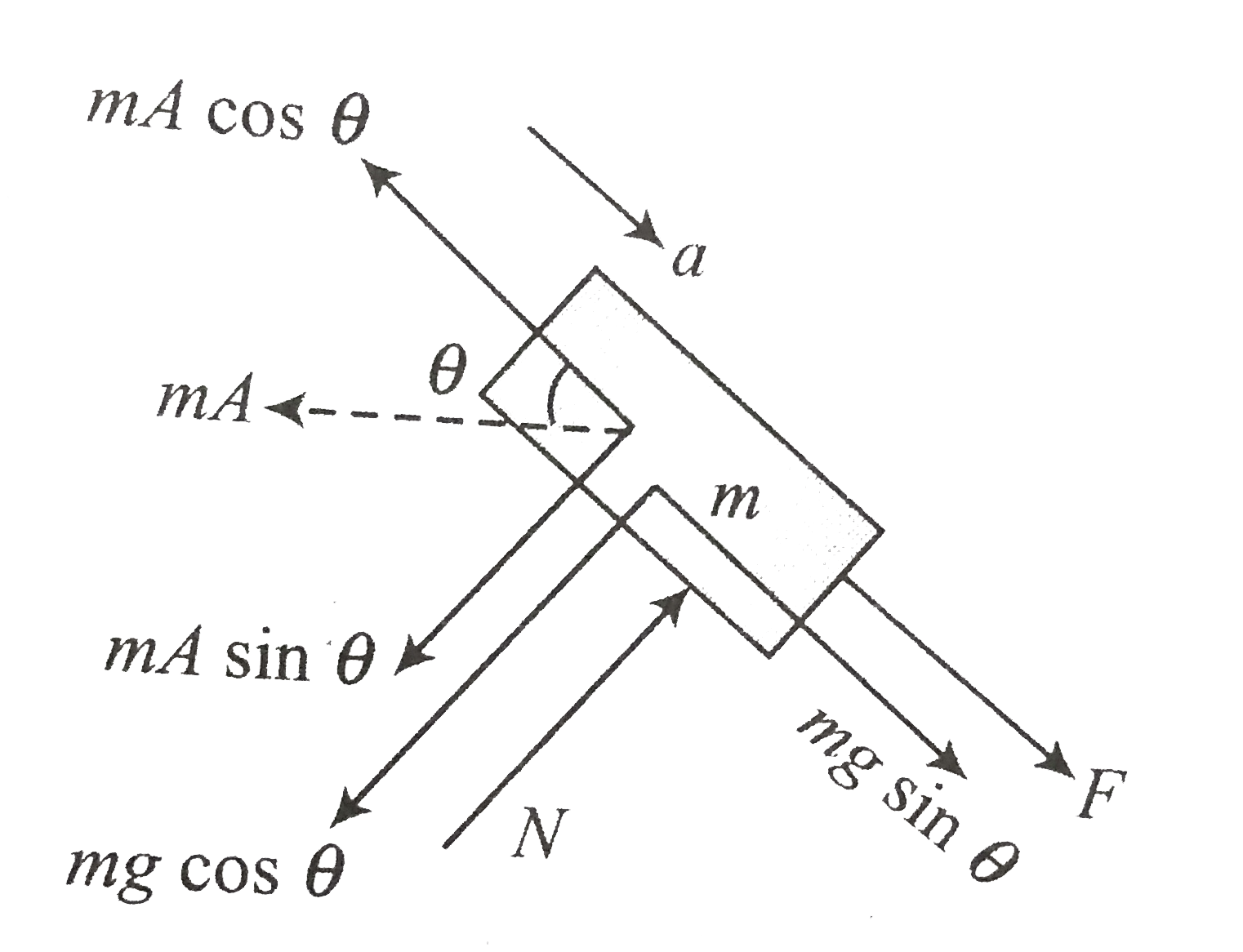
Method -1: Let the acceleration of block relative to wedge be →amM=→a and acceleration of wedge on ground be −→aM=→A. Free body diagram as in fig.

Equation of motion of M,
F−Nsinθ−Fcosθ=MA ...(i)
Equation of motion of m in y-direction,
N−mgcosθ=may=mAsinθ ..(ii)
Substituting the value of N from (ii) in (i), we can get the value of A.
A=F(1−cosθ)−mgsinθcosθM+msin2θ
Method 2: If we make the FBD of m w.r.t. M, pseudo force mA is to be applied because M is non-inertial. W.r.t. M, there is no acceleration of m in y-direction, so balancing the forces in y-direction.
N=mgcosθ+mAsinθ
which is same as (ii).
Method 3: Taking block and wedge as system.
External force acting in horizontal direction is F.
ΣFx=m(am)x+M(aM)x

Let the acceleration of block w.r.t. wedge is a. or |→am,M|=a
(→am)x=(→am,M)x+(→aM)x
∣∣(→am)x∣∣=acosθ+A
Hence,
F=m(acosθ+A)+MA
Now analyzing the sloping surface and writing equation w.r.t ground,
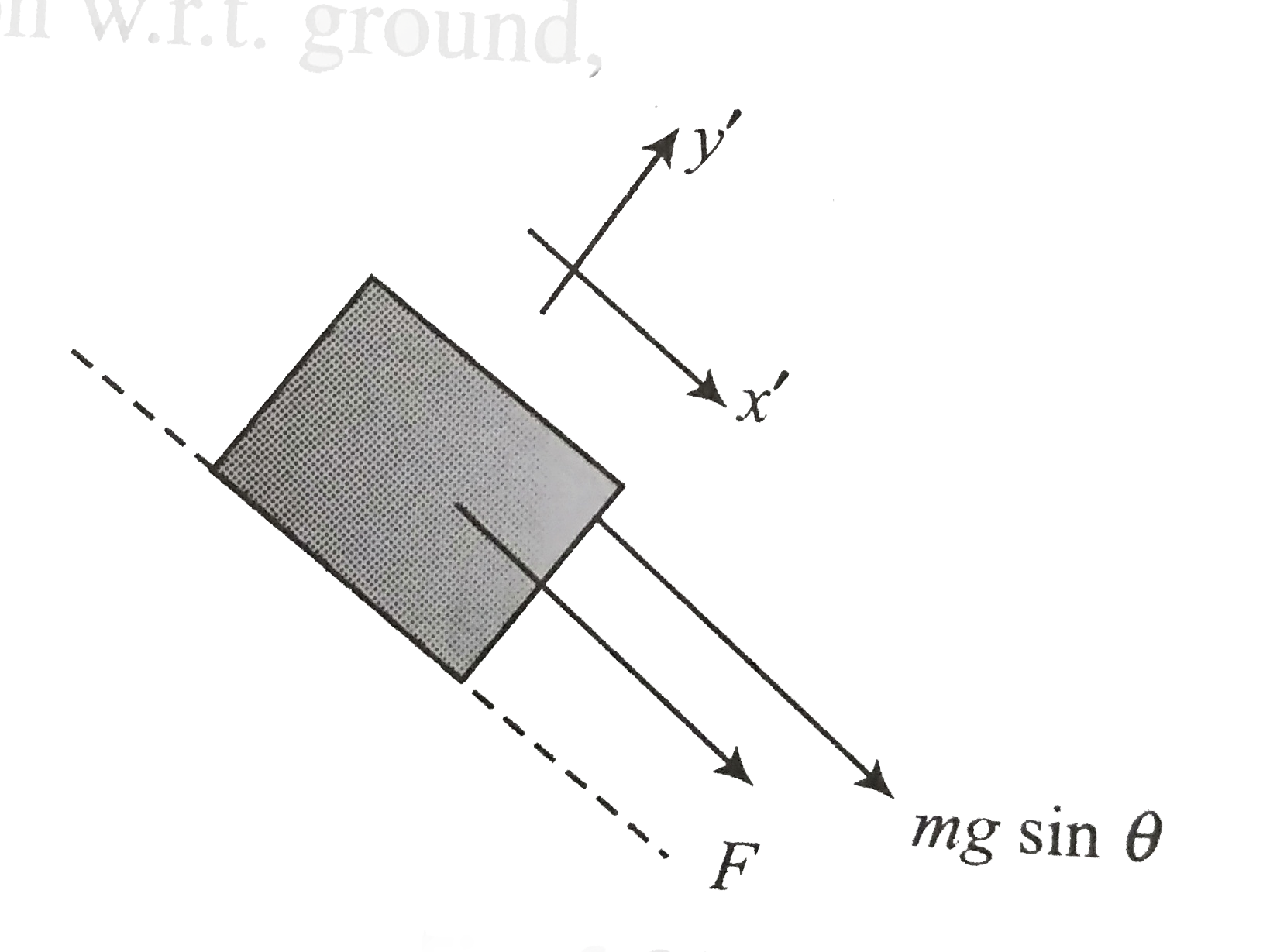
Σ→Fx'=m(→am)x'
(→am)x'=(→am,M)x'+(→am)x'
=a+Acosθ
F+mgsinθ=m(a+Acosθ) ...(ii)
From (i) and (ii) ,
A=F(1−cosθ)−mgsinθcosθM+msin2θ.
Topper's Solved these Questions
- NEWTON'S LAWS OF MOTION 1Book:CENGAGE PHYSICS ENGLISHChapter:NEWTON'S LAWS OF MOTION 1Exercise:Exercise 6.1
Explore 11 Videos
- NEWTON'S LAWS OF MOTION 1Book:CENGAGE PHYSICS ENGLISHChapter:NEWTON'S LAWS OF MOTION 1Exercise:Exercise 6.2
Explore 35 Videos
- NEWTON'S LAWS OF MOTION 1Book:CENGAGE PHYSICS ENGLISHChapter:NEWTON'S LAWS OF MOTION 1Exercise:Integer
Explore 5 Videos
- MISCELLANEOUS VOLUME 2Book:CENGAGE PHYSICS ENGLISHChapter:MISCELLANEOUS VOLUME 2Exercise:INTEGER_TYPE
Explore 10 Videos
- NEWTON'S LAWS OF MOTION 2Book:CENGAGE PHYSICS ENGLISHChapter:NEWTON'S LAWS OF MOTION 2Exercise:Integer type
Explore 1 Video
Similar Questions
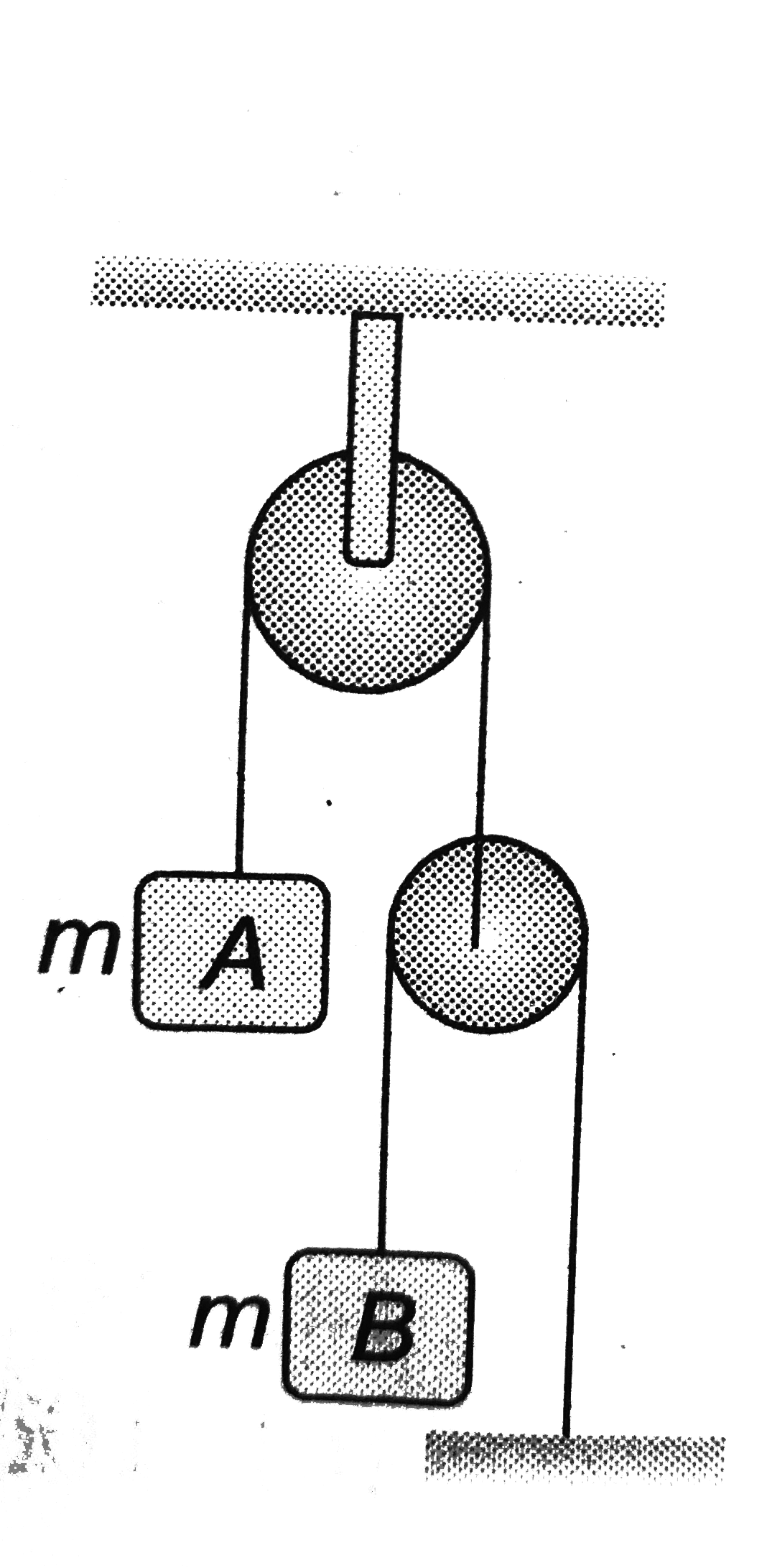
In the figure shown neglecting friction and mass of pulley, what is the acceleration of mass B ?
View SolutionAll the surfaces are smooth as shown in figure. The acceleration of mass m relative to wedge is :

View SolutionIn fig. mass m is being pulled on the incline of a wedge of mass M. All the surfaces are smooth. Find the acceleration of the wedge.

View SolutionA block of mass 'm' is kept on a smooth moving wedge. If the acceleration of the wedge is 'a'
View SolutionA wedge of mass M=4m lies on a frictionless plane. A particle of mass m approaches the wedge with speed v. there is no friction between the particle and the plane or between the particle and the wedge. The maximum height climbed by the particle on the wedge is given by
View SolutionIn the arrangement shown in figure the masses of the wedge M and the body m are known. The appreciable friction exists only between the wedge and the body m, the friction coefficient being equal to k. The masses of the pulley and the thread are negligible. Find the acceleration of the body m relative to the horizontal surface on which the wedge slides.

View SolutionBlock A of mass m and block B of mass 2m are placed on a fixed triangular wedge by means of a light and inextensible string and a frictionless pulley as shown in fig . The wedge is inclined at 45∘ to the horizontal on both sides . The coefficient of friction between the block Aand the wedge is 2/3 and that between the block B and the wedge is 1/3 .If the system of AandB is released from rest then find .
a. the acceleration of A
b. tension in the string
c.the magnitude and direction of the frictional force acting on A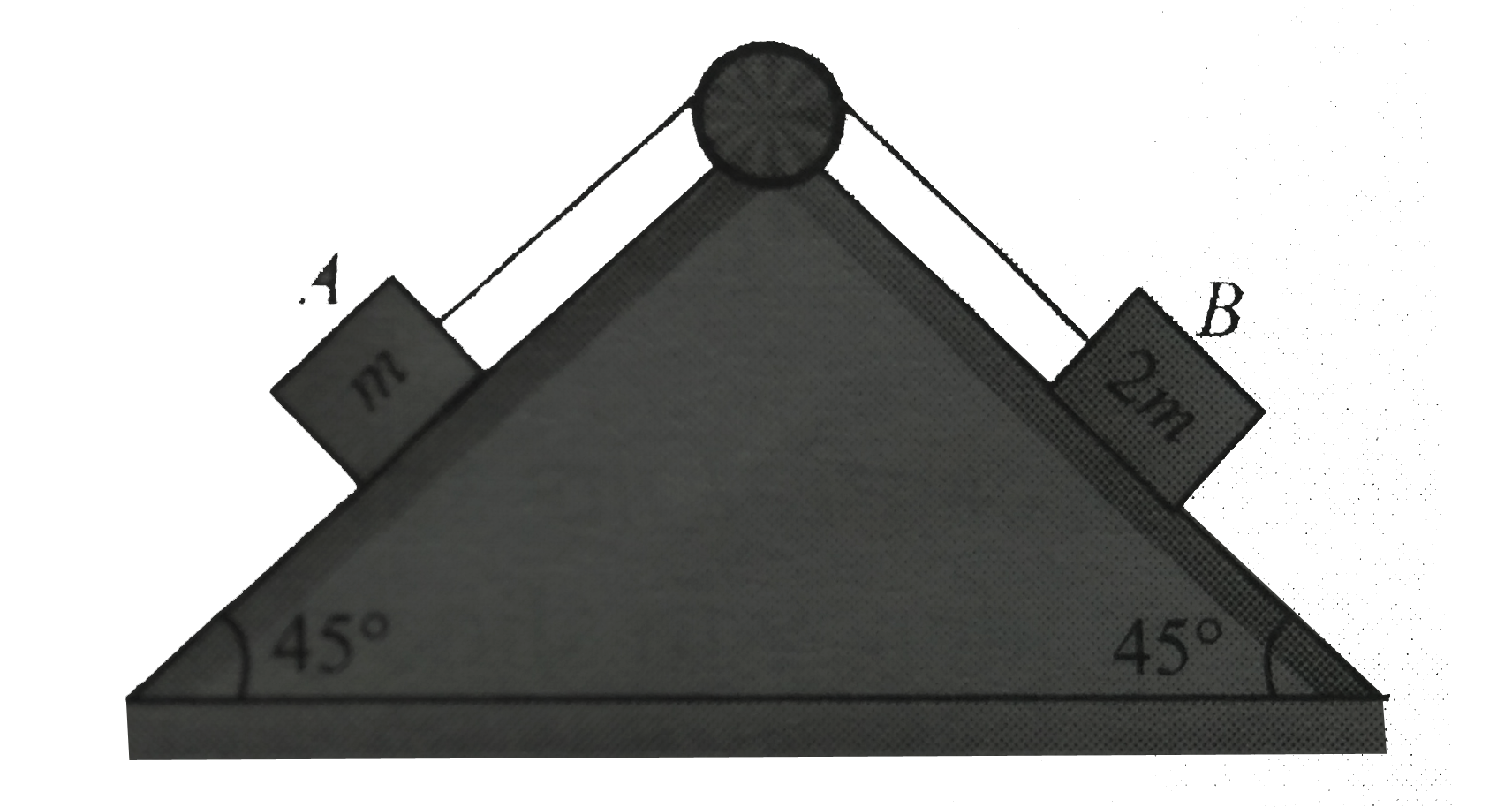
View SolutionNeglect friction. Find acceleration of m,2mand3m as shown in the figure. The wedge is find.

View SolutionA block of mass m is released from a wedge of mass m as shown in figure . Find the time taken by the block to reach the end of the wedge.
View SolutionIn the figure-2.61 a bar of mass m is on the smooth inclined face of the wedge of mass M,the inclination to the horizontal being 0.The wedge is resting on a smooth horizontal plane.Assuming the pulley to be smooth and the string is light and inextensible. Find the acceleration of M,when M and m are always in contact.

View Solution