In the figure-2.61 a bar of mass m is on the smooth inclined face of the wedge of mass M,the inclination to the horizontal being 0.The wedge is resting on a smooth horizontal plane.Assuming the pulley to be smooth and the string is light and inextensible. Find the acceleration of M,when M and m are always in contact.

Let x1→ distance of the pulley (wedge) from the wall.
x2→ distance of the bar from the pulley.
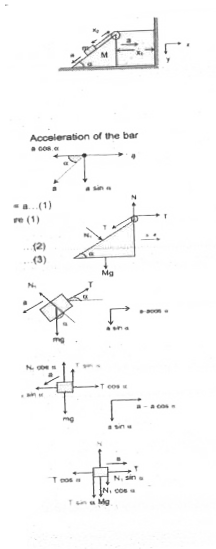
Therefore x1+x2=l
d2x1dt2→ acceleration of wedge
d2x1dt2=−d2x2dt2
d2x2dt2→ acceleration of the bar, w.r.t. wedge
∣∣∣d2x1dt2∣∣∣=∣∣∣d2x2dt2∣∣∣= a (say).
Net acceleration of wedge along the horizontal surface = a.... (1)
Net acceleration of bar along the horizontal surface figure (1)
=a− comp. of acceleration of bar w.r.t. wedge
=a−acosα ...(2)
Vertically downward =asinα ...(3)
Forces on wedge and bar are shown separately in figure(2) and fig. (3) respectively (4) and (5).
From the F.B.D. of the wedge Along the chosen X-direction T+N1sinα−Tcosα=Ma ...(4)
along Y-direction
For bar
N1cosα+Tsinα+Mg−N=0 ...(5)
From the F.B.D. of the bar along X-direction
cosα−N1sinα=m.(a−acosα) ...(6)
For Wedge: along y-direction
mg−N1cosα−Tsinα=masinα ...(7)
From equations (4), (5), (6) and (7) eliminating other quantities we can fing a. The problem can be solved by choosing X-Y axis for the system along and normal to the surface of wedge. Just do by yourself.
Hence answer is mgsinαM+2m(1−cosα)
Similar Questions
A block of mass 'm' is kept on a smooth moving wedge. If the acceleration of the wedge is 'a'
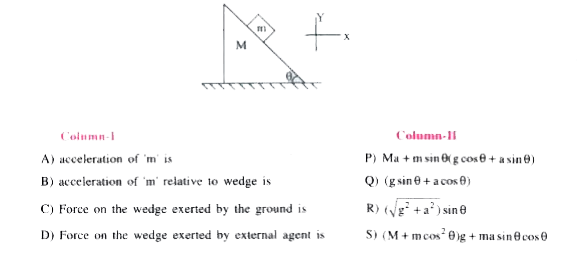
View SolutionA block of mass m is placed at rest on a smooth wedge of mass M placed at rest on a smooth horizontal surface. As the system is released

View SolutionIn the arrangement shown in fig. pulleys are smooth and massless. Threads are massless and inextensible. Find acceleration of mass m1.

View SolutionIn fig. mass m is being pulled on the incline of a wedge of mass M. All the surfaces are smooth. Find the acceleration of the wedge.

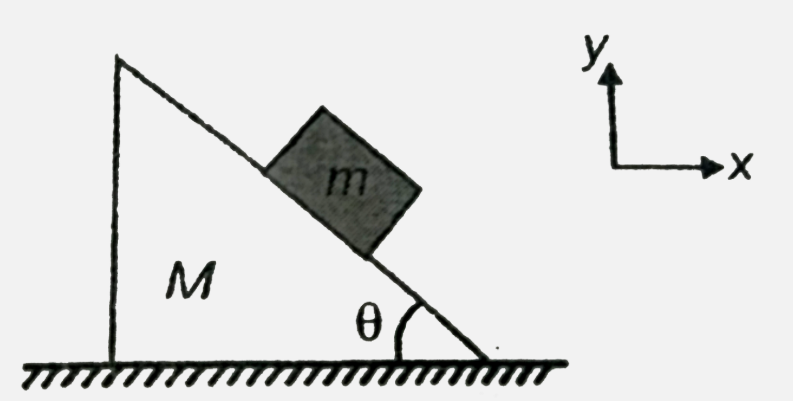
View SolutionA block of mass m is placed on a smooth inclined plane of inclination θ with the horizontal. The force exerted by the plane on the block has a magnitude
View SolutionA block of mass m is placed on a smooth inclined plane of inclination θ with the horizontal. The force exerted by the plane on the block has a magnitude
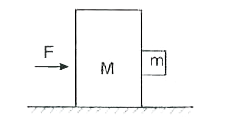
View SolutionA horizontal force F pushes wedge of mass M on a smooth horizontal surface. A block of mass m is stationary to the wedge, then:
View SolutionA smooth block of mass m is held stationary on a smooth wedge of mass M and inclination θ as shown in figure .If the system is released from rest , then the normal reaction between the block and the wedge is

View SolutionA block of mass 2kg slides down the face of a smooth 45∘ wedge of mass 9kg as shown in the figure. The wedge is placed on a frictionless horizontal surface. Determine the acceleration of the wedge.

View SolutionA block of mass m is placed on a smooth wedge of mass M, as shown in the figure . Just after placiing block m over wedge M.
View Solution
