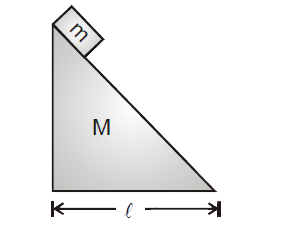
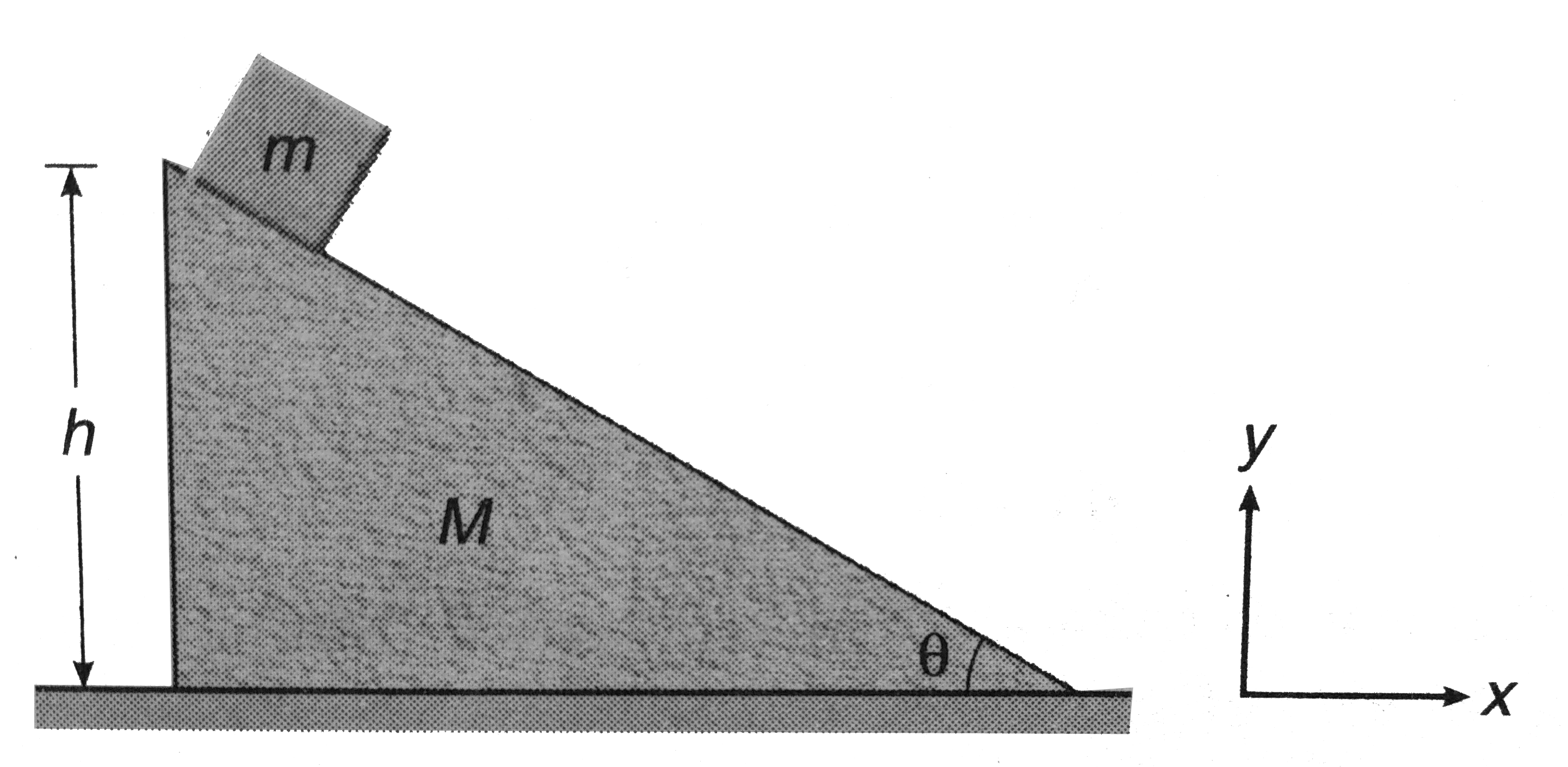
A small block of mass m is placed at rest on the top of a smooth wedge of mass M, which in turn is placed at rest on a smooth horizontal surface as shown in figure. It h be the height of wedge and θ is the inclination, then the distance moved by the wedge as the block reaches the foot of the wedge is
MhcotθM+m
(b) mhcotθM+m
(c) MhcosecθM+m
(d) mhcosecθM+m
The correct Answer is:B
Horizontal side of wedge is hcotθ.
(##DCP_V02_CH11_E01_098_S01.png" width="80%">
Mx=m(hcotθ−x)
∴ x=mhcotθM+m
Topper's Solved these Questions
- CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONBook:DC PANDEYChapter:CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONExercise:Level 1 Subjective
Explore 32 Videos
- CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONBook:DC PANDEYChapter:CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONExercise:Level 1 Subjective Questions
Explore 1 Video
- CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONBook:DC PANDEYChapter:CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONExercise:Level 1 Assertion and Reason
Explore 15 Videos
- CENTRE OF MASS, IMPULSE AND MOMENTUMBook:DC PANDEYChapter:CENTRE OF MASS, IMPULSE AND MOMENTUMExercise:Comprehension type questions
Explore 15 Videos
- CIRCULAR MOTIONBook:DC PANDEYChapter:CIRCULAR MOTIONExercise:Medical entrances s gallery
Explore 19 Videos
Similar Questions
A particle of mass m is placed at rest on the top of a smooth wedge of mass M, which in turn is placed at rest on a smooth horizontal surface as shown in figure. Then the distance moved by the wedge as the particle reaches the foot of the wedge is :
View SolutionA block of mass m is placed at rest on a smooth wedge of mass M placed at rest on a smooth horizontal surface. As the system is released

View Solution
Knowledge Check
A block of mass m rests on a stationary wedge of mass M. The wedge can slide freely on a smooth horizontal surface as shown in figure. If the block starts from rest
 A(a) the position of the centre of mass of the system will changeB(b) the position of centre of mass of the system will change along the vertical but not along the horizontalC(c) the total energy of the system will remain constantD(d) All of the above
A(a) the position of the centre of mass of the system will changeB(b) the position of centre of mass of the system will change along the vertical but not along the horizontalC(c) the total energy of the system will remain constantD(d) All of the aboveA block of mass 2kg slides down the face of a smooth 45∘ wedge of mass 9kg as shown in the figure. The wedge is placed on a frictionless horizontal surface. Determine the acceleration of the wedge.
 A2ms−2B11√2ms−2C1ms−2Dnone of these
A2ms−2B11√2ms−2C1ms−2Dnone of theseA block of mass m is placed at the top of a smooth wedge ABC. The wedge is rotated about an axis passing through C as shown in the figure - 3.81. The minimum value of angular speed ω such that the block does not slip on the wedge is :
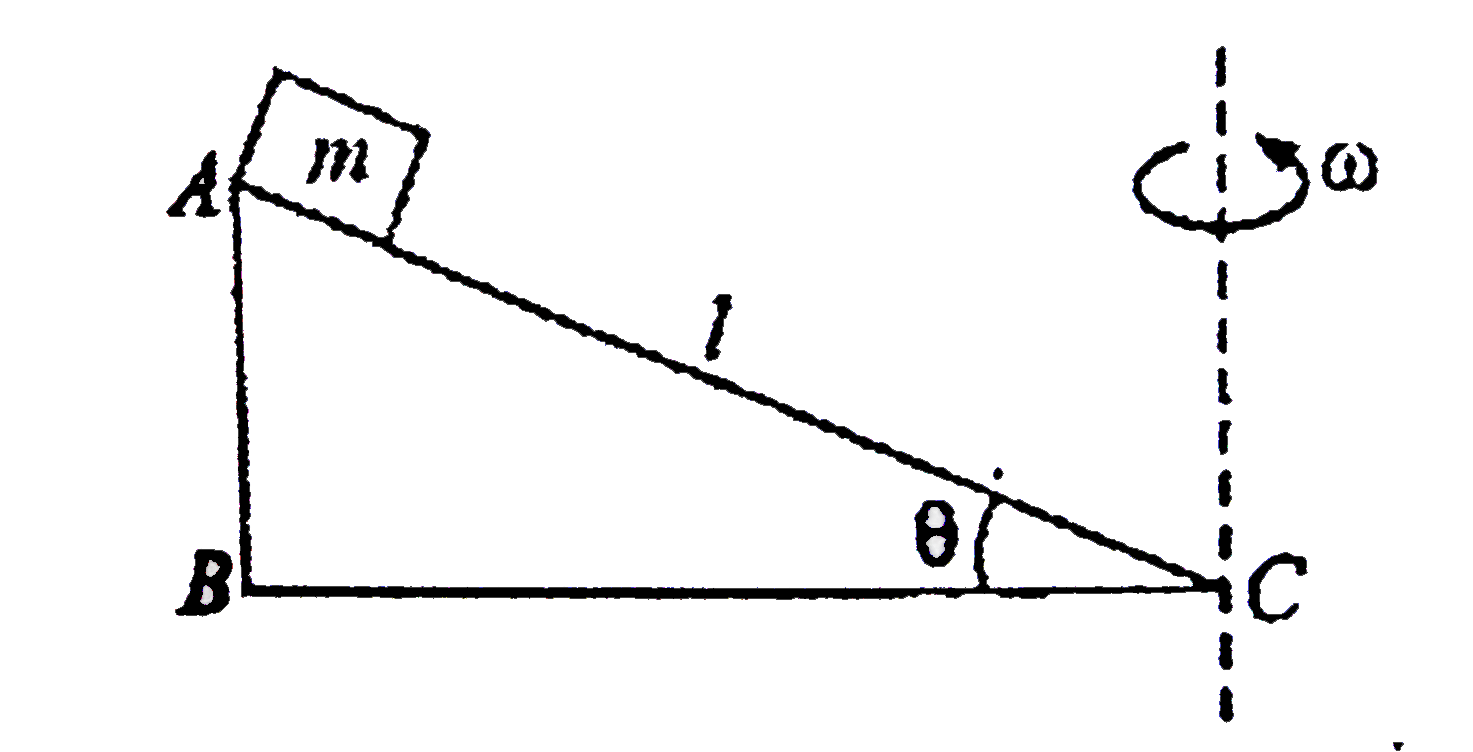 A⎛⎝√gsinθl⎞⎠secθB(√gl)cosθC(√glcosθ)cosθD√gsinθl
A⎛⎝√gsinθl⎞⎠secθB(√gl)cosθC(√glcosθ)cosθD√gsinθl
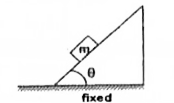
A block of mass m is at rest over the rough surface of the fixed wedge.

View SolutionA block of mass m is placed at the bottom of a massless smooth wedge which if placed on a horizontal surface. When we push the wedge with a constant force, the block moves up the wedge. Find the work done by the external agent when the block has a speed v and is reaches the top of the wedge.

View SolutionA block of mass m slides over a smooth wedge of mass M which is placed over a rough horizontal surface . The centre of mass of the system will move towards left

Here μ = coefficient of friction between the wedge and the ground .
View SolutionA block of mass m is released from the top of a wedge of mass M as shown in figure. Find the displacement of wedges on the horizontal ground when the block reaches the bottom of the wedges. Neglect friction everywhere.
View SolutionA block of mass m rests on a wedge of mass M which, in trun, rests on a horizontal table, as shown in figure. All surfaces are frictionless. If the system starts at rest with point P of the block a distance h above the table, find the speed of the wedge the instant point P touches the table.
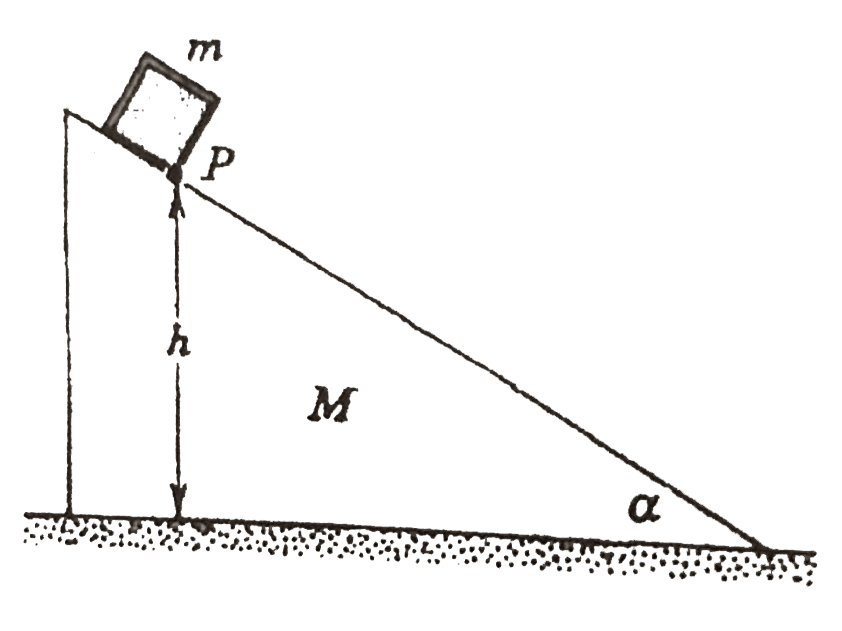
View Solution

