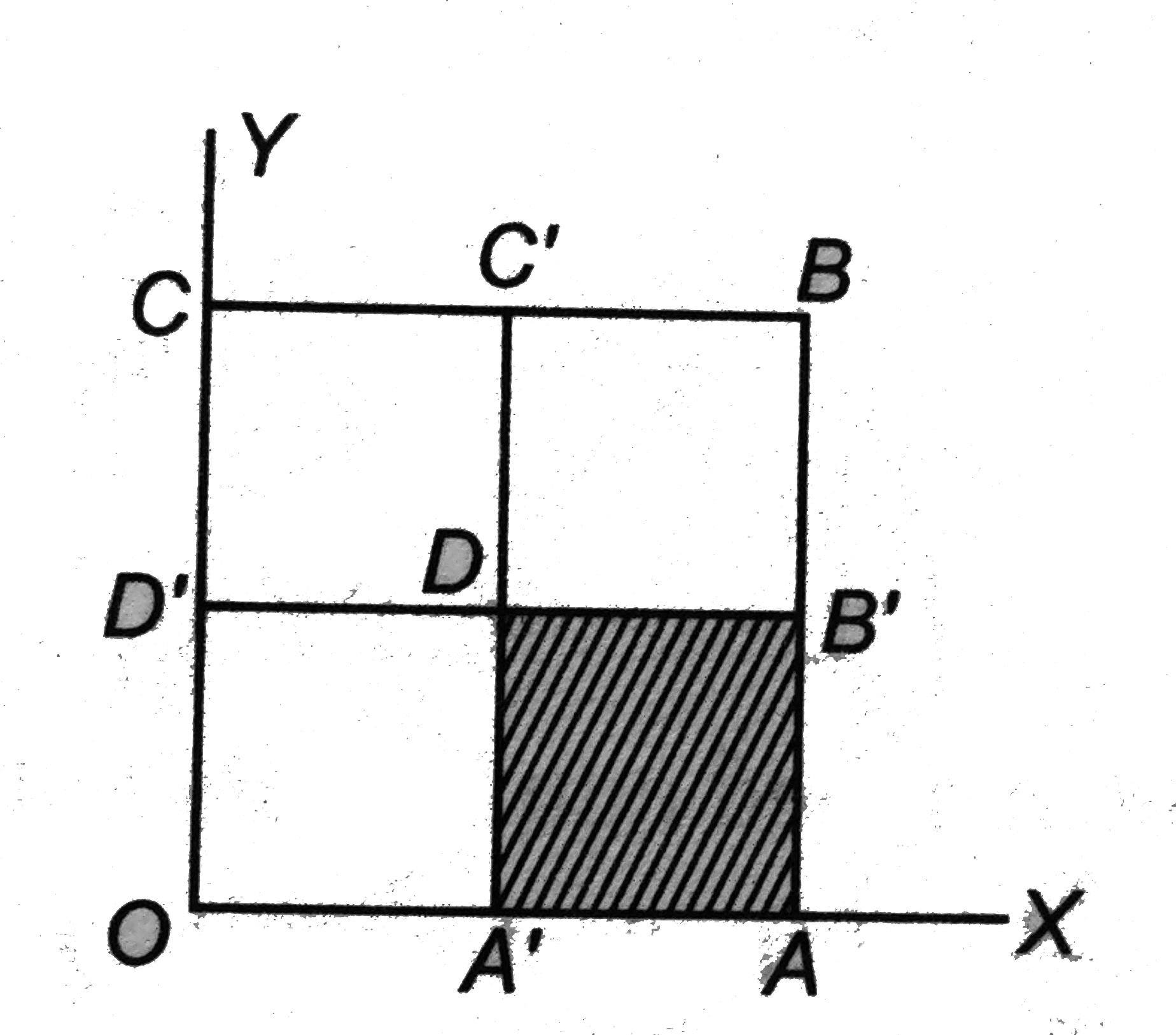
A square of side 2cm and uniform thickness is divided into four squares. The square portion A′AB′D is removed and the removed portion is placed over the portion DB′BC′. The new position of centre of mass is
(2cm,2cm)
(2cm,3cm)
(2cm,2.5cm)
(3cm,3cm)
The correct Answer is:C
xCM=A1x1+A2x2+A3x3+A4x4A1+A2+A3+A4
=(4)(1)+(4)(1)+(4)(3)+(4)(3)16=2cm
yCM=A1y1+A2y2+A3y3+A4y4A1+A2+A3+A4
=(4)(1)+4(3)+4(3)+4(3)16=2.5cm
Topper's Solved these Questions
- CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONBook:DC PANDEYChapter:CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONExercise:Level 1 Subjective
Explore 32 Videos
- CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONBook:DC PANDEYChapter:CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONExercise:Level 1 Subjective Questions
Explore 1 Video
- CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONBook:DC PANDEYChapter:CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONExercise:Level 1 Assertion and Reason
Explore 15 Videos
- CENTRE OF MASS, IMPULSE AND MOMENTUMBook:DC PANDEYChapter:CENTRE OF MASS, IMPULSE AND MOMENTUMExercise:Comprehension type questions
Explore 15 Videos
- CIRCULAR MOTIONBook:DC PANDEYChapter:CIRCULAR MOTIONExercise:Medical entrances s gallery
Explore 19 Videos
Similar Questions
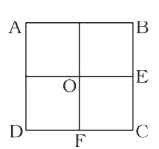
A square of side 4m having uniform thickness is divided into four equal squares as shown in Fig. If one of the squares is cut off, find

the position of centre of mass of the remaining portion from the centre O.
View SolutionA square of side 4 cm and of uniform thickness is divided into four equal squares. If one of them is cut off (OECF), then the position of the centre of mass of the remaining portion from O is √2kcm . Find the value of K.
View Solution
Knowledge Check
A square of side a and uniform thickness is divided into four equal parts. If upper right part is removed, then find the coordinates of centre of mass of remaining part.
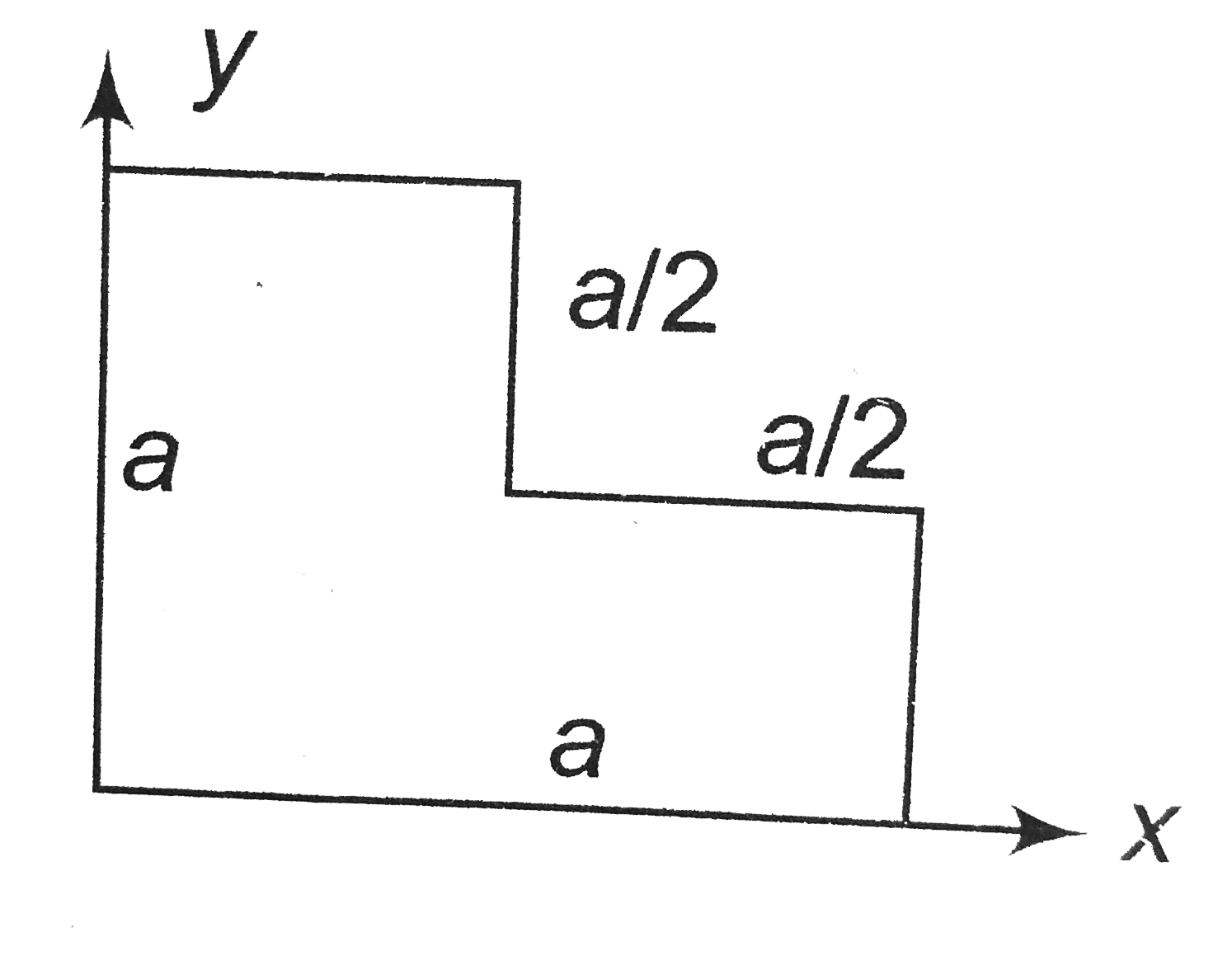 .A(512a,512a)B(712a,712a)C(14a,14a)D(13a,13a)
.A(512a,512a)B(712a,712a)C(14a,14a)D(13a,13a)A circular plate of uniform thickness has a diameter of 28cm. A circular portion of diameter 21cm is removed from the plate as shown. Ois the centre of mass of complete plate. The position of centre of mass of remaining portion will shift towards left from 'O' by
 A5cmB9cmC4.5cmD5.5cm
A5cmB9cmC4.5cmD5.5cmA square of side a2 is removed from a disc having radius a . Find centre of mass of remaing portion.
 Ax=(−2aπe)B(−a8πe−2)C(−4a3πe)D(−a3πe−4)
Ax=(−2aπe)B(−a8πe−2)C(−4a3πe)D(−a3πe−4)
A circular plate of unifrom thickness has a diameter of 56cm. A circular portion of diameter 42cm is removed from the edge of the plate as shown in Fig. Find the position of centre of mass of the remaining portion.

View SolutionA circular plate of unifrom thickness has a diameter of 56cm. A circular portion of diameter 42cm is removed from the edge of the plate as shown in Fig. Find the position of centre of mass of the remaining portion.

View SolutionA uniform circular plate of uniform thickness has a diameter of 56 cm. A circular portion of diameter 42 cm is removed from the edge of the plate. Find the position of the centre of mass of the remaining portion.
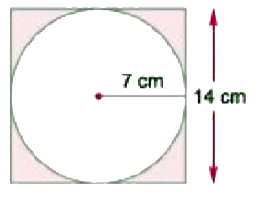
View SolutionFind the area of shaded portion if each side of the square is 14 cm.
View Solution
From a uniform square plate of side a and mass m, a square portion DEFG of side a2 is removed. Then, the moment of inertia of remaining portion about the axis AB is
View Solution

