Find the area of shaded portion if each side of the square is 14 cm.
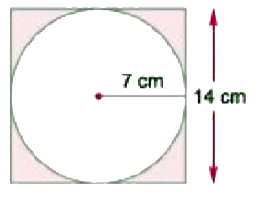
50 sq cm
45 sq cm
62 sq cm
42 sq cm
The correct Answer is:D
Step by step video, text & image solution for Find the area of shaded portion if each side of the square is 14 cm. by Maths experts to help you in doubts & scoring excellent marks in Class 14 exams.
Updated on:21/07/2023Topper's Solved these Questions
- AREA AND PERIMETERBook:ARIHANT SSCChapter:AREA AND PERIMETERExercise:FAST TRACK TECHENIQUES
Explore 133 Videos
- APPROXIMATIONBook:ARIHANT SSCChapter:APPROXIMATIONExercise:Fast Track Practice
Explore 74 Videos
- AVERAGE Book:ARIHANT SSCChapter:AVERAGE Exercise:EXERCISE HIGHER SKILL LEVEL QUESTION
Explore 30 Videos
Similar Questions
Find the area of the shaded portion.

View SolutionFour equal circles are described about the four corners of square so that each touches two of the others, as shown in the figure. Find the area of the shaded region, if each side of the square measures 14 cm.

View SolutionFind the area of shaded region of area under the square of side 14cm
View SolutionFour equal circles are described about the four corners of a square so that each touches two of the others as shown in Fig. 15.38. Find the area of the shaded region, each side of the square measuring 14 cm. (FIGURE)
View SolutionIn the given figure, four equal circles are described about corners of a square so that each circle touches two of the circles as shown in the figure. Find the area of the shaded region, each side of the square measuring 14 cm.
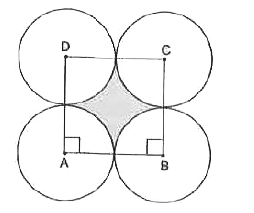
View SolutionIn the given figure, find the area of shaded region if ABCD is a square of side 14cm and APD and BPC are semicircles.

View SolutionIn the figure, square ABCD is inscribed in the sector A-PCQ. The radius of sector C-BXD is 20 cm. Complete the following activity to find the area of the shaded portion.
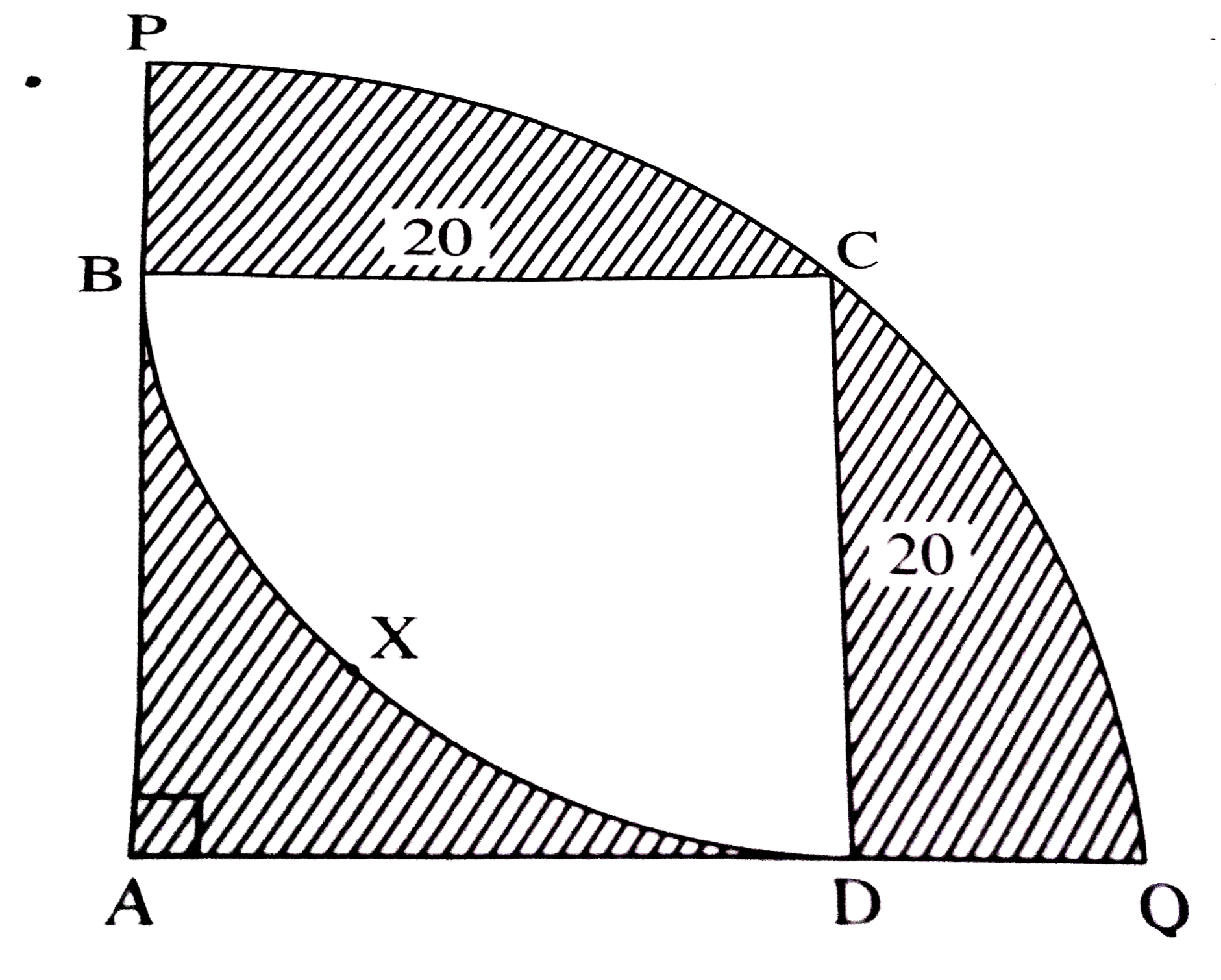
Side of the square ABCD = radius of sector C-BXD = 20 cm
Area of square =side2=400cm2
Area of sector C-BXD =θ360×πr2
=□360×3.14×202=□cm2
Area of the shaded portion inside square
= Area of square - A (sector C- BXD)
=400−□cm2
Radius of sector A-PCQ= Length of diagonal of square ABCD
r1=20√2cm
Area of the shaded region outside square
= A(sector A-PCQ)-A (square ABCD)
=90360×3.14×(20√2)2−200
=□cm2
∴ total area of shaded portion = area of shaded portion inside square + area of shaded portion outside square =□cm2
View SolutionFind the area of the shaded portions in the following figures
View SolutionFind the area of the shaded portion in the following figures.
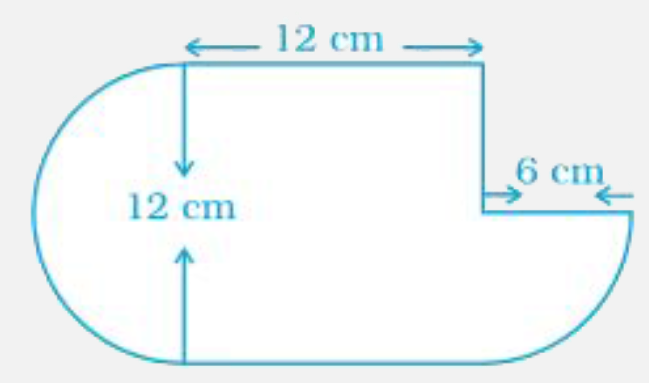
View SolutionFind the area of the shaded portion in the following figures.
View Solution