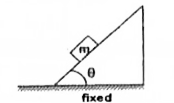
A block of mass m is at rest over the rough surface of the fixed wedge.

Video Solution

Text Solution

Verified by Experts

$(A) \to (q) (B) \to (p) (C) \to (s) (D) \to (r)$

Updated on:21/07/2023

A small block of mass $m$ is placed at rest on the top of a smooth wedge of mass M, which in turn is placed at rest on a smooth horizontal surface as shown in figure. It h be the height of wedge and $θ$ is the inclination, then the distance moved by the wedge as the block reaches the foot of the wedge is

A $\frac{M h cot θ}{M + m}$
B(b) $\frac{m h cot θ}{M + m}$
C(c) $\frac{M h cos e c θ}{M + m}$
D(d) $\frac{m h cos e c θ}{M + m}$
A small block of mass m is kept on the inclined surface of a wedge of mass M. The inclined surface of the wedge makes an angle $θ$ with the horizontal. The wedge is kept on a frictionless rigid horizontal floor. You can neglect friction between the block and the wedge also. An external agent applies a horizontal force F on the wedge.

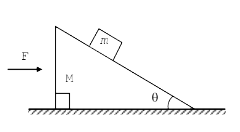
The value of the force F so that the wedge remains at rest is $F_{1}$ . Which of the options is incorrect?
A $F_{1}$ is less than mg sin $θ$
B $F_{1}$ is less then mg cos $θ$
C $F_{1}$ does not depend on M
DIt is not possible to keep the wedge at rest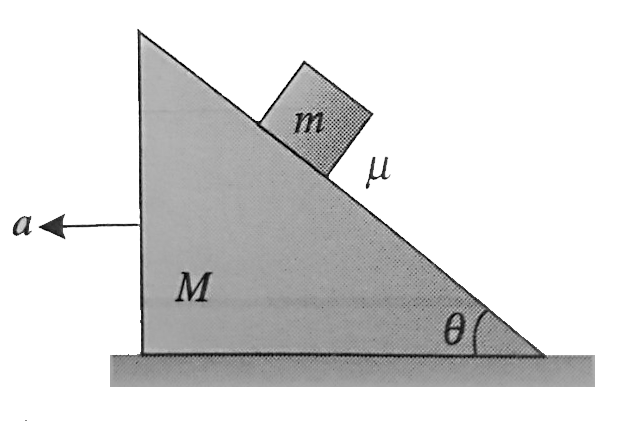
A block of mass m is at rest relative to the stationary wedge of mass M. The coefficient of friction between block and wedge is $μ$ . The wedge is now pulled horizontally with acceleration a as shown in figure. Then the minimum magnitude of a for the friction between block and wedge to be zero is:
A $> a n θ$
B $μ > a n θ$
C $g cot θ$
D $μ g cot θ$