In fig. mass m is being pulled on the incline of a wedge of mass M. All the surfaces are smooth. Find the acceleration of the wedge.

Constraint relation
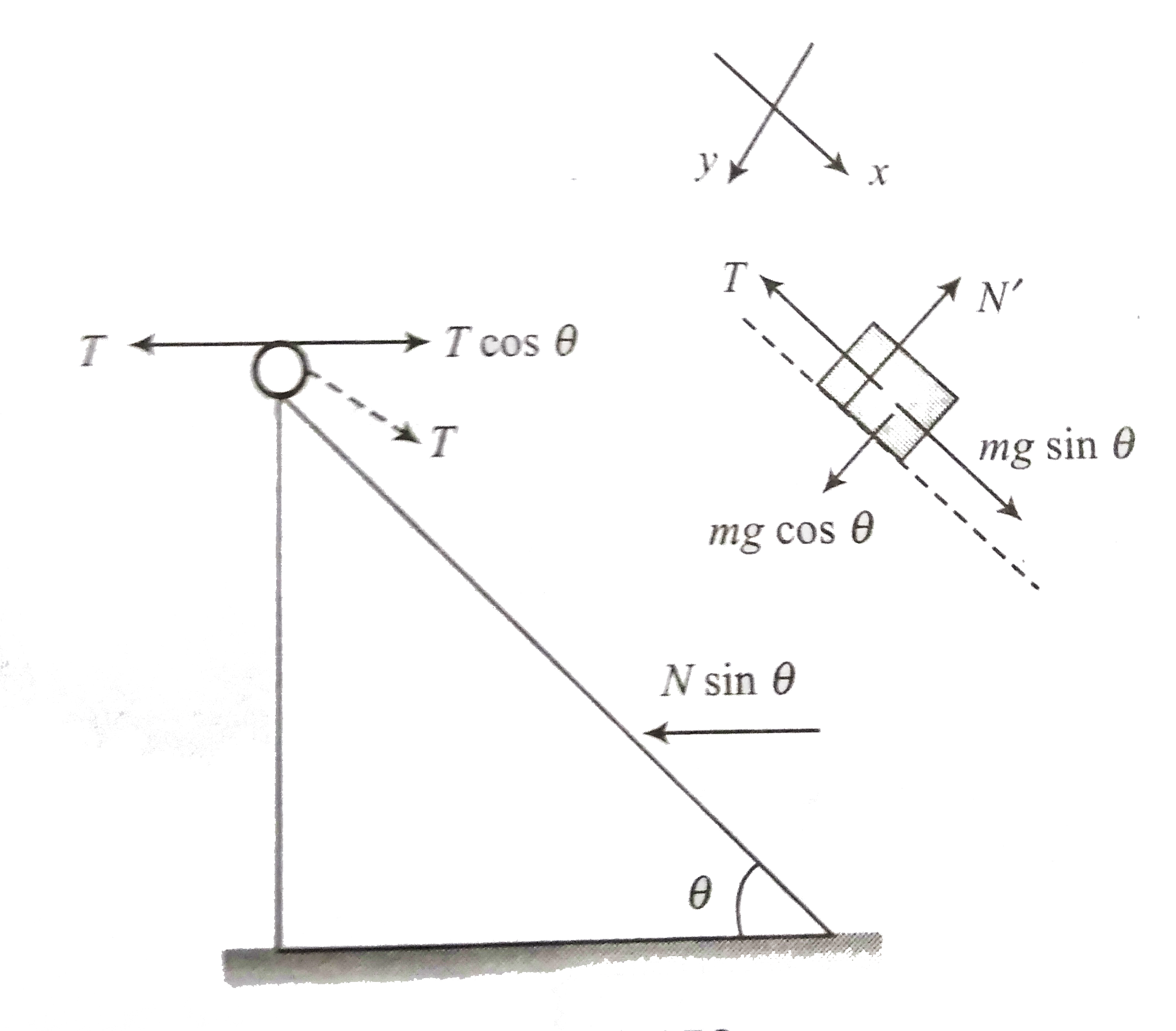
It is clear from above discussion
ax=A(1−cosθ)
and ay=Asinθ
Equations of motion
Considering the motion of wedge in horizontal direction
For wedge
T=Tcosθ+Nsinθ=MA
Considering the motion of block parallel and perpendicular to the sloping side in horizontal direction
For block: In the direction parallel to inclined surface,
mgsinθ−T=max=MA(1−cosθ)
or T=mgsinθ=MA(1−cosθ) ...(ii) In the direction perpendicular to inclined plane,
mgcosθ−N=may=mAsinθ
N=mgcosθ=mAsinθ ...(iii)
Substituting the value of N from (ii) and (iii) in (i) we get,
A=mgsinθM+2m(1−cosθ).
Topper's Solved these Questions
- NEWTON'S LAWS OF MOTION 1BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - NEWTON'S LAWS OF MOTION 1EXERCISE - Solved Examples
11 Videos
- NEWTON'S LAWS OF MOTION 1BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - NEWTON'S LAWS OF MOTION 1EXERCISE - Exercise 6.1
11 Videos
- MISCELLANEOUS VOLUME 2BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - MISCELLANEOUS VOLUME 2EXERCISE - INTEGER_TYPE
10 Videos
- NEWTON'S LAWS OF MOTION 2BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - NEWTON'S LAWS OF MOTION 2EXERCISE - Integer type
1 Video
Similar Questions
In the arrangement shown in the figure , the rod of mass m held by two smooth walls , remain always perpendicular to the surface of the wedge of mass M . Assuming all the surface are frictionless, find the acceleration of the rod wedge.

View SolutionA block of mass 'm' is kept on a smooth moving wedge. If the acceleration of the wedge is 'a'
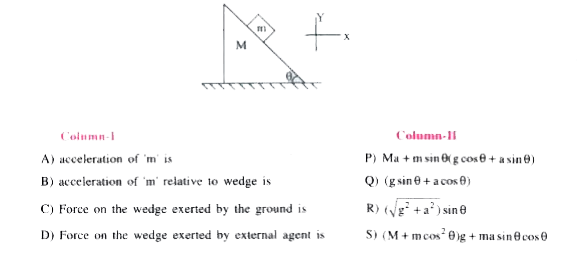
View SolutionA block of mass m is placed on the inclined sufrace of a wedge as shown in fig. Calculate the acceleration of the wedge and the block when the block is released. Assume all surfaces are frictionless.

View SolutionA block of mass M is connected with a particle of mass m by a light inextensible string as shown in fig. Assuming all contaction surfaces as smooth, find the acceleration of the wedge after releasing the system.

View SolutionA block of mass 'M' is placed on the top of a wedge of mass '4M'. All the surfaces are frictionless. The system is released from rest. The distance moved by the wedge at the instant, the block reaches the bottom will be

View SolutionIn the arrangement shown in figure, the rod of mass mheld by two smooth walls, remains always perpendicular to the surface of the wedge of mass M. Assumming all the surface to be frictionless, find the acceleration of the rod and that of the wedge.

View SolutionAll the surfaces are smooth as shown in figure. The acceleration of mass m relative to wedge is :

View SolutionA block of mass m=5kg is placed on the wedge of mass M=32kg as shown in the figure. Find the acceleration of wedge with respect to ground. (Neglect any type of friction. Spring and pulley are ideal)

View SolutionA small block of mass m is kept on the inclined surface of a wedge of mass M. The inclined surface of the wedge makes an angle θ with the horizontal. The wedge is kept on a frictionless rigid horizontal floor. You can neglect friction between the block and the wedge also. An external agent applies a horizontal force F on the wedge.
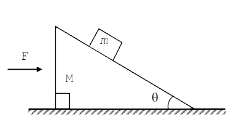
The value of the force F so that the wedge remains at rest is F1. Which of the options is incorrect?
View SolutionA small block of mass m is kept on the inclined surface of a wedge of mass M. The inclined surface of the wedge makes an angle θ with the horizontal. The wedge is kept on a frictionless rigid horizontal floor. You can neglect friction between the block and the wedge also. An external agent applies a horizontal force F on the wedge.

The value of the force F so that the wedge remains at rest is F1. Which of the options is incorrect?
View Solution
