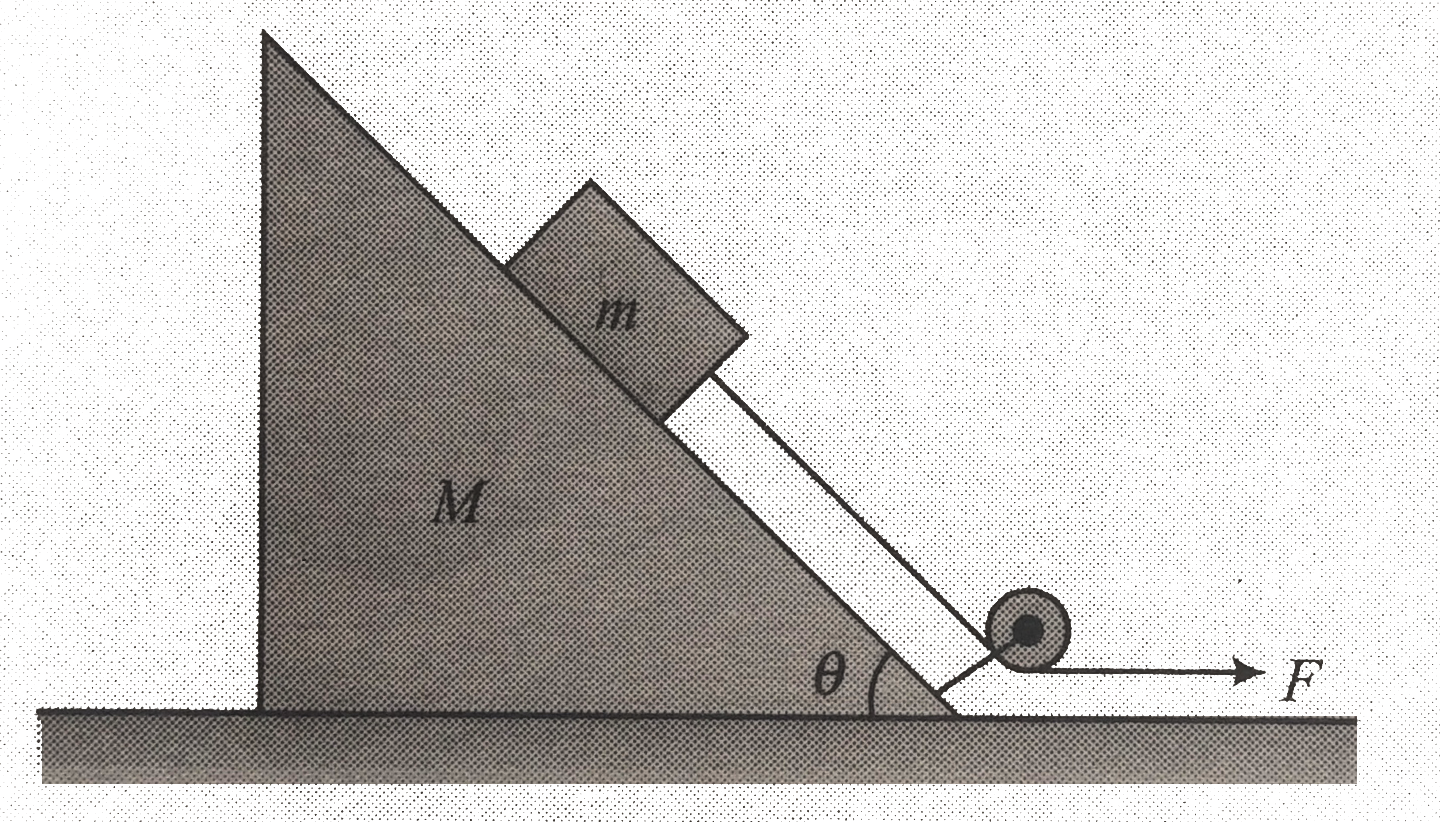
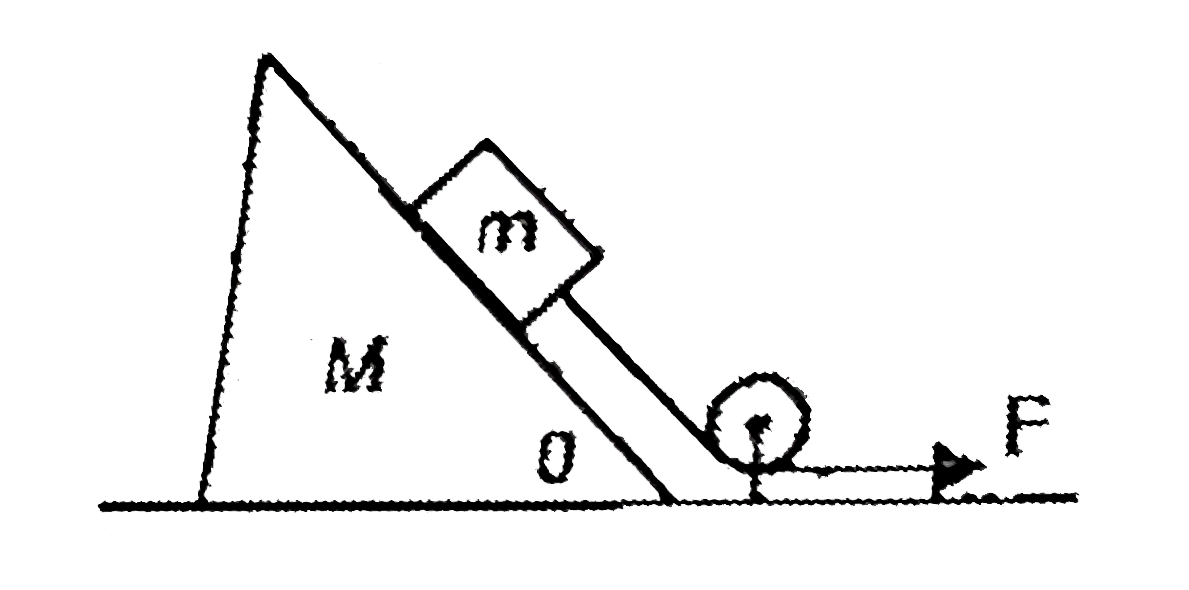
In fig. mass m is being pulled on the incline of a wedge of mass M. All the surfaces are smooth. Find the acceleration of the wedge.
a=F(1−cosθ)mg2sinθcosθM+2msin2θ
a=F(1+cosθ)+mgsinθcosθM+msin2θ
a=F(1−cosθ)−mgsinθcosθM+msin2θ
a=F(1+cosθ)−mgsinθcosθM−msin2θ
The correct Answer is:C
Method -1: Let the acceleration of block relative to wedge be →amM=→a and acceleration of wedge on ground be −→aM=→A. Free body diagram as in fig.
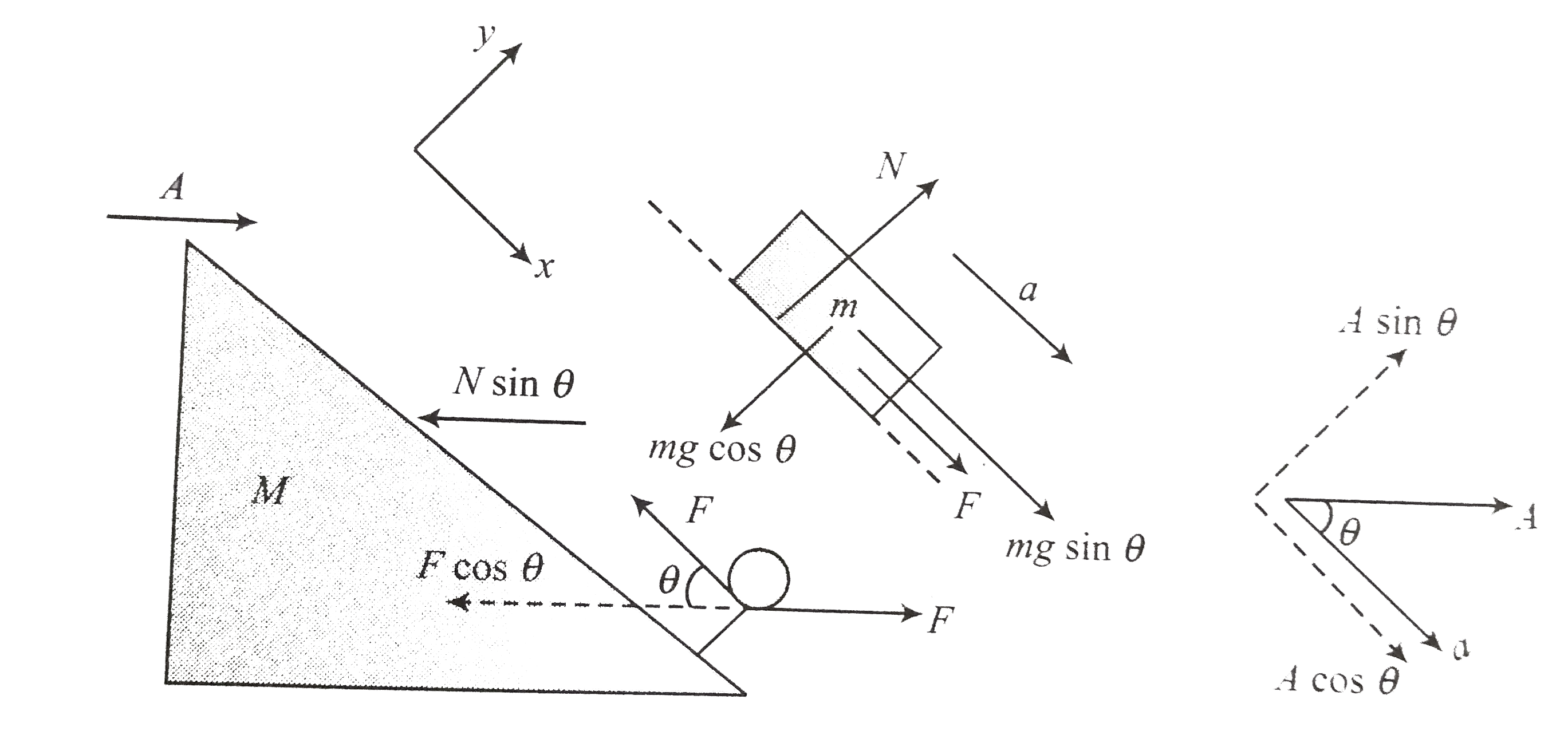
Equation of motion of M,
F−Nsinθ−Fcosθ=MA ...(i)
Equation of motion of m in y-direction,
N−mgcosθ=may=mAsinθ ..(ii)
Substituting the value of N from (ii) in (i), we can get the value of A.
A=F(1−cosθ)−mgsinθcosθM+msin2θ
Method 2: If we make the FBD of m w.r.t. M, pseudo force mA is to be applied because M is non-inertial. W.r.t. M, there is no acceleration of m in y-direction, so balancing the forces in y-direction.
N=mgcosθ+mAsinθ
which is same as (ii).
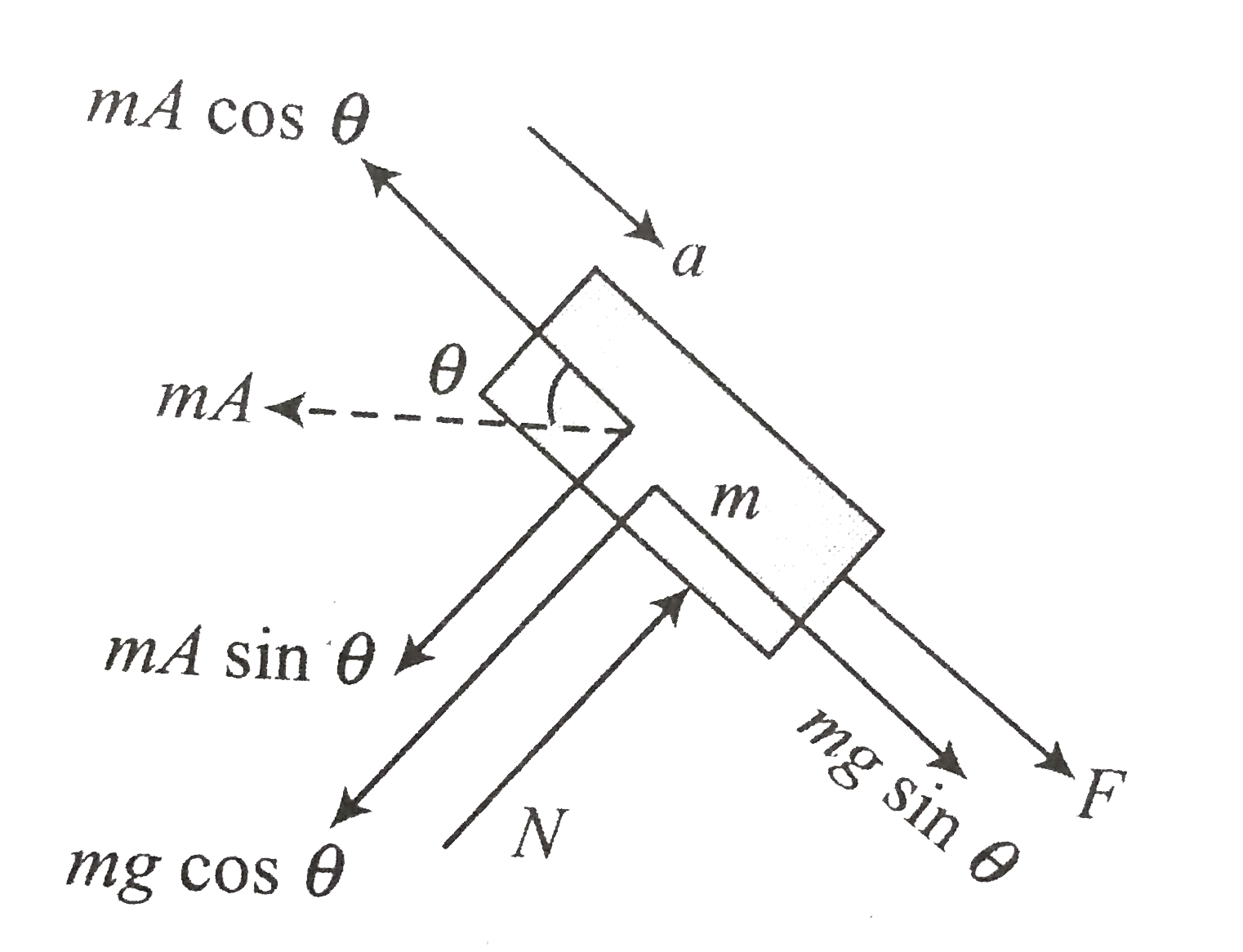
Method 3: Taking block and wedge as system.
External force acting in horizontal direction is F.
ΣFx=m(am)x+M(aM)x

Let the acceleration of block w.r.t. wedge is a. or |→am,M|=a
(→am)x=(→am,M)x+(→aM)x
∣∣(→am)x∣∣=acosθ+A
Hence,
F=m(acosθ+A)+MA
Now analyzing the sloping surface and writing equation w.r.t ground,
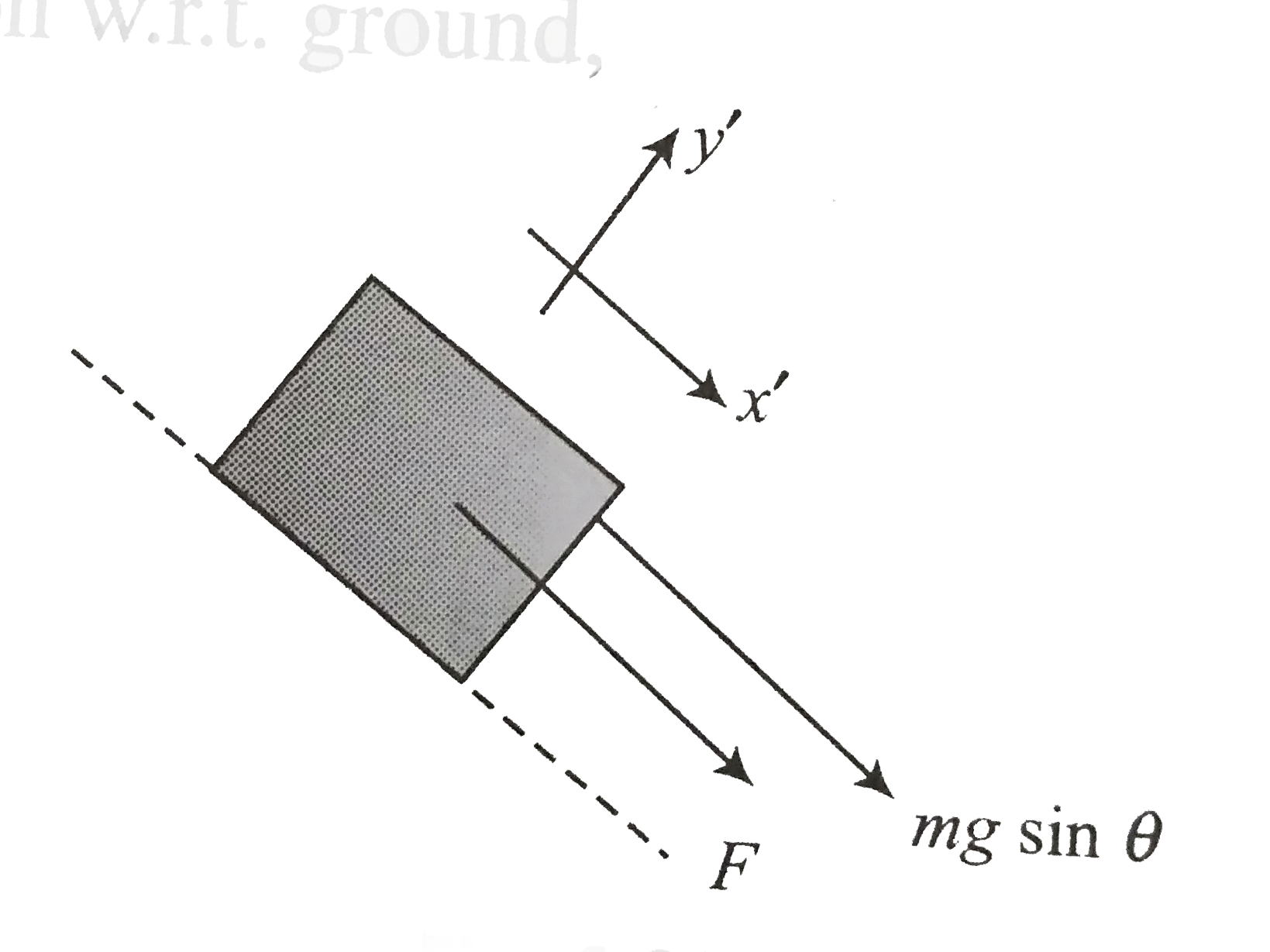
Σ→Fx'=m(→am)x'
(→am)x'=(→am,M)x'+(→am)x'
=a+Acosθ
F+mgsinθ=m(a+Acosθ) ...(ii)
From (i) and (ii) ,
A=F(1−cosθ)−mgsinθcosθM+msin2θ.
Topper's Solved these Questions
- NEWTON'S LAWS OF MOTION 1Book:CENGAGE PHYSICSChapter:NEWTON'S LAWS OF MOTION 1Exercise:Exercise 6.1
Explore 11 Videos
- NEWTON'S LAWS OF MOTION 1Book:CENGAGE PHYSICSChapter:NEWTON'S LAWS OF MOTION 1Exercise:Exercise 6.2
Explore 35 Videos
- NEWTON'S LAWS OF MOTION 1Book:CENGAGE PHYSICSChapter:NEWTON'S LAWS OF MOTION 1Exercise:Integer
Explore 5 Videos
- MISCELLANEOUS VOLUME 2Book:CENGAGE PHYSICSChapter:MISCELLANEOUS VOLUME 2Exercise:INTEGER_TYPE
Explore 10 Videos
- NEWTON'S LAWS OF MOTION 2Book:CENGAGE PHYSICSChapter:NEWTON'S LAWS OF MOTION 2Exercise:Integer type
Explore 1 Video
Similar Questions
In the Fig. shown, mass 'm' is being pulled on the incline of a wedge of mass M. All the surface are smooth. Find the acceleration of the wedge.
View SolutionIn the arrangement shown in figure, the rod of mass m held by two smooth walls, remains always perpendicular to the surface of the wedge of mass M. Assuming all the surface to be frictionless, find the acceleration of the rod and that of the wedge.

View Solution
Knowledge Check
All surfaces are smooth. The acceleration of mass m relative to the wedge is
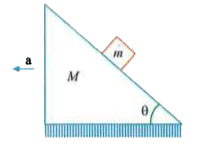 AgsinθBgsinθ+acosθCgsinθ−acosθDacosθ
AgsinθBgsinθ+acosθCgsinθ−acosθDacosθAll surfaces are smooth The acceleration of mass m relative to the wedge is
 .AgsinθBgsinθ+acosθCgsinθ−acosθDacosθ
.AgsinθBgsinθ+acosθCgsinθ−acosθDacosθAll the surfaces are smooth as shown in figure. The acceleration of mass m relative to wedge is :
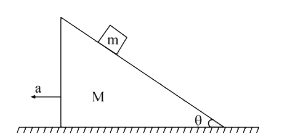 Ag sin θBg sin θ + a cos θCg sin θ - a cos θDa cos θ
Ag sin θBg sin θ + a cos θCg sin θ - a cos θDa cos θ
Figure-2.54 shows a block of mass m is placed on an inclined wedge of mass M If the system is released from rest find the acceleration of m and M.
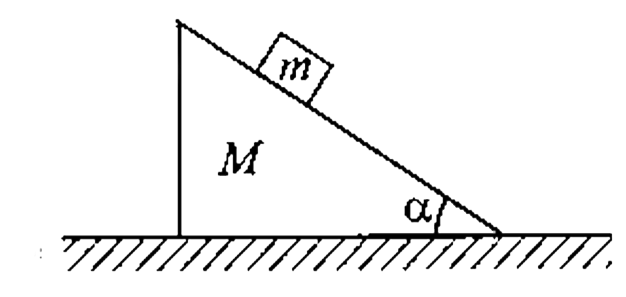
View SolutionA block of mass m is placed on the inclined sufrace of a wedge as shown in fig. Calculate the acceleration of the wedge and the block when the block is released. Assume all surfaces are frictionless.

View SolutionA block of mass M is connected with a particle of mass m by a light inextensible string as shown in fig. Assuming all contaction surfaces as smooth, find the acceleration of the wedge after releasing the system.

View SolutionIn the arrangement shown in figure, the rod of mass mhelp by two smooth walls, remains always perpendicular to the surface of the wedge of mass M. Assuumming all the surface to be frictionless, find the acceleration of the rod and that of the wedge.

View SolutionIn the arrangement shown in figure wedge of mass M moves towards left with an acceleration a. All surfaces are smooth. The acceleration of mass m relative to wedge is

View Solution

