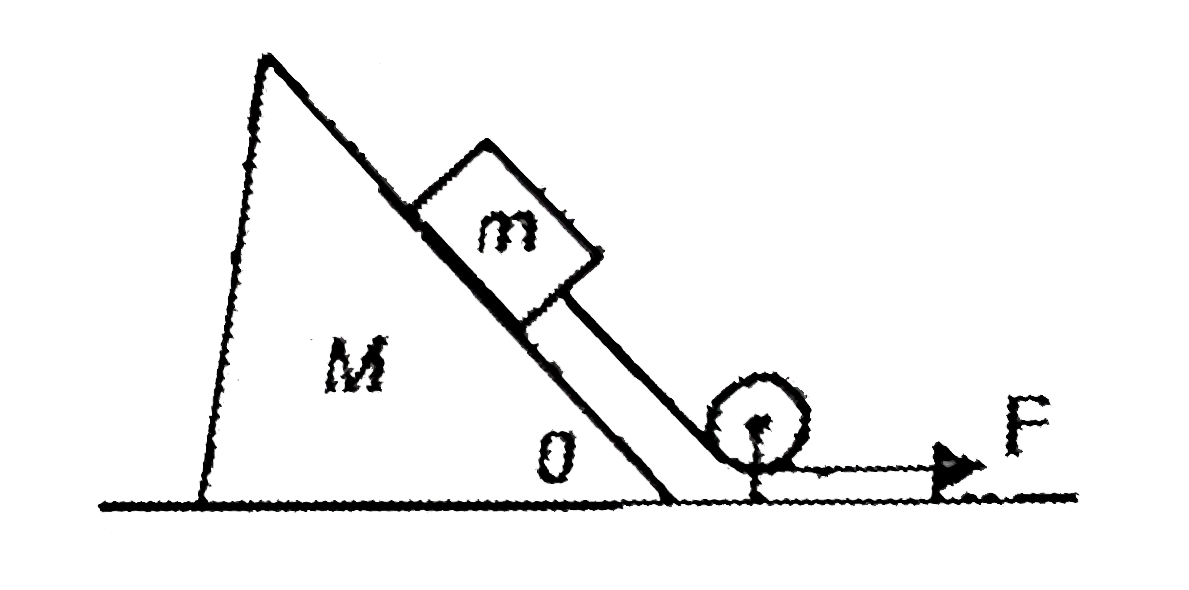
A block of mass M is connected with a particle of mass m by a light inextensible string as shown in fig. Assuming all contaction surfaces as smooth, find the acceleration of the wedge after releasing the system.

From the constraint relationship shown in fig.
y+4x=l
⇒dydt+4dxdt=0
⇒d2ydt+4d2xdt=0
⇒a2=4a1 (numerically)...(i)
Where a1 is the acceleration fo M and a2 is the acceleration of m, with respect to M.
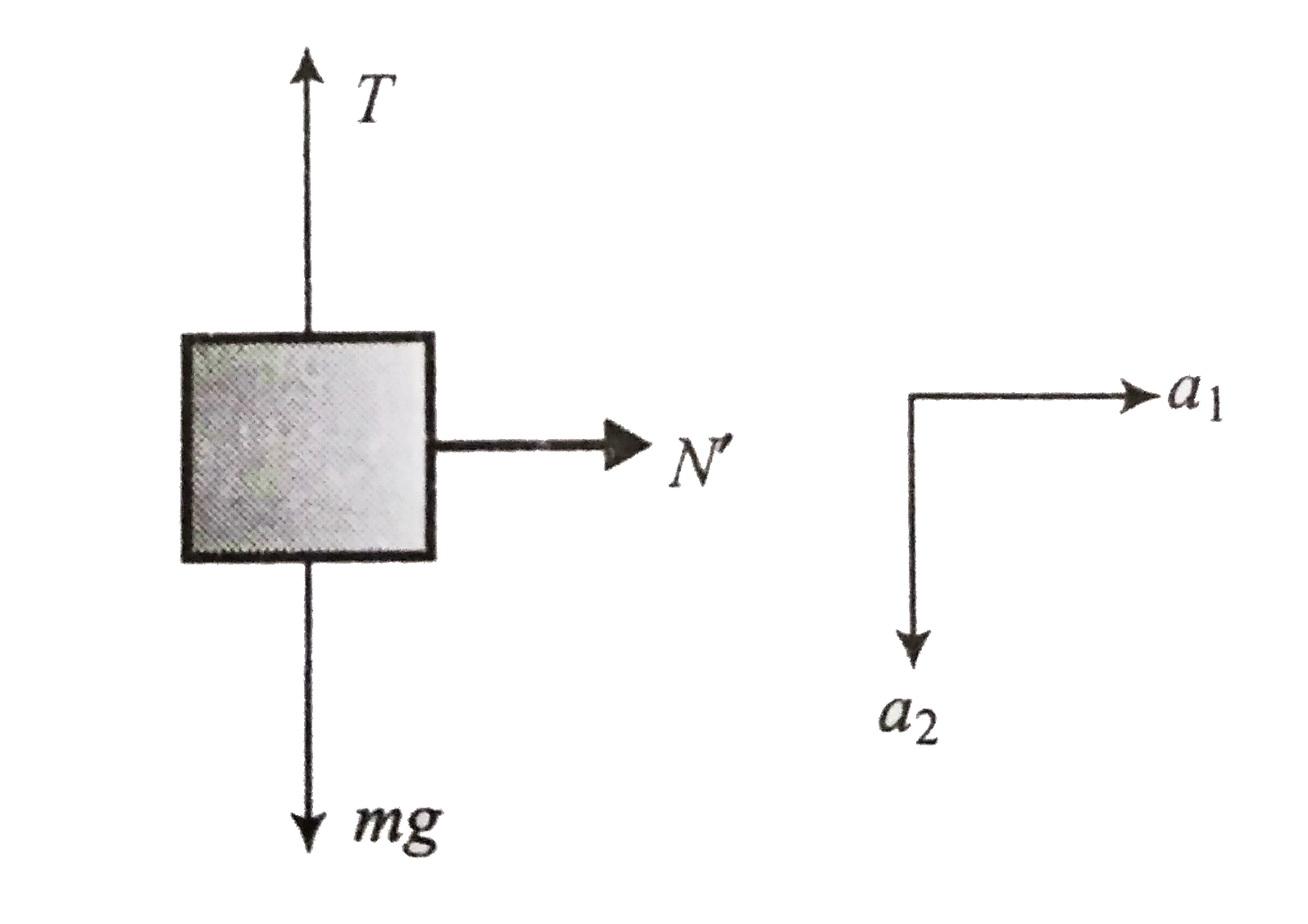
Equation for M
ΣFx=Ma1⇒4T−N'=Ma1 ...(ii)

For m,ΣFy=ma2⇒mg−T=ma2 ...(iii)
ΣFx=ma1⇒N'=ma1 ...(iv)
(ii)+(iv) ⇒a1=4TM+m ...(v)
Putting a2=4a1 from (i) and T=(M+m)a14
From (v) in (iii) we obtain
mg−(M+m)a14=m(4a1)
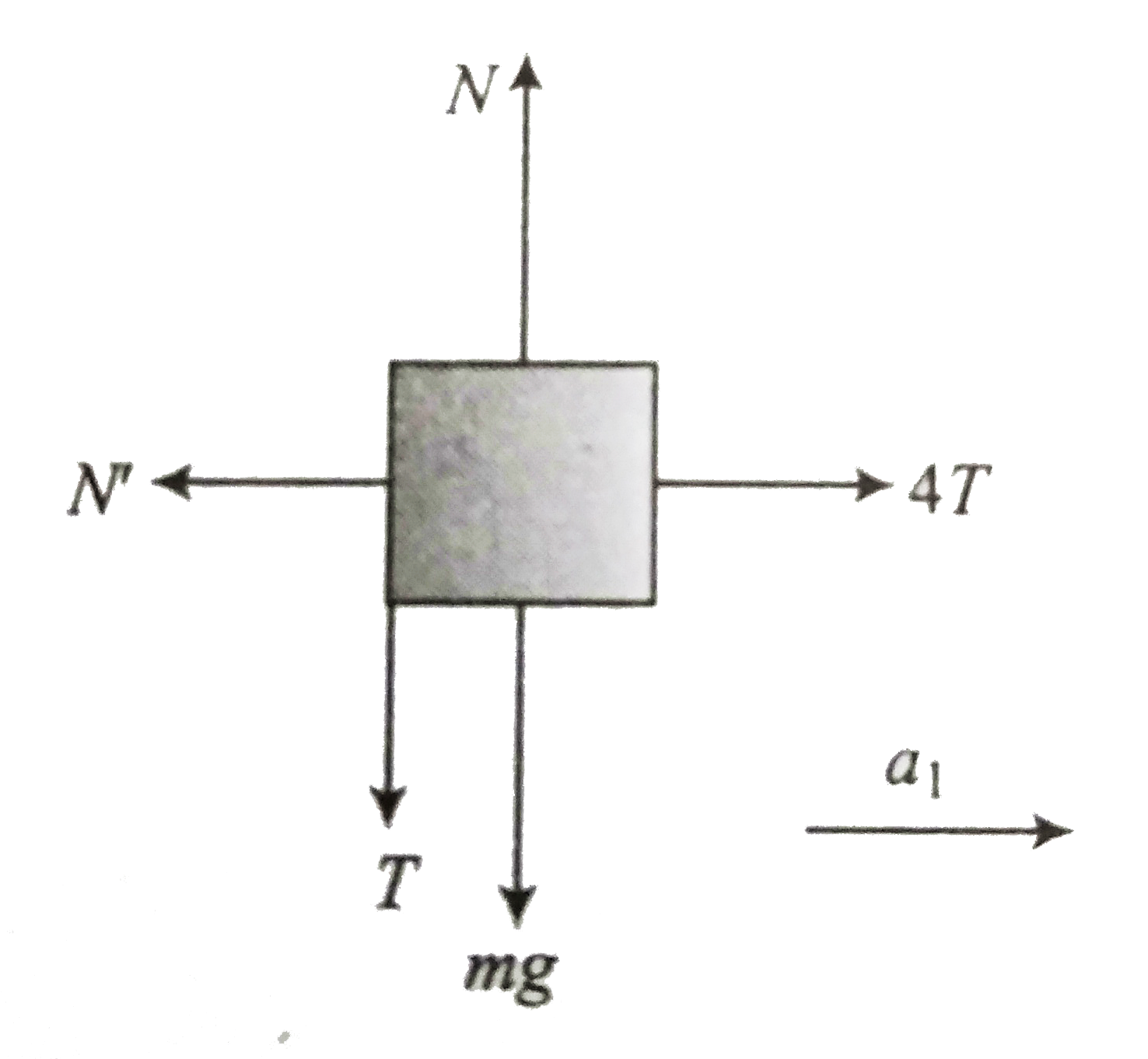
⇒a1=4mgM+17m.
Topper's Solved these Questions
- NEWTON'S LAWS OF MOTION 1Book:CENGAGE PHYSICSChapter:NEWTON'S LAWS OF MOTION 1Exercise:Solved Examples
Explore 11 Videos
- NEWTON'S LAWS OF MOTION 1Book:CENGAGE PHYSICSChapter:NEWTON'S LAWS OF MOTION 1Exercise:Exercise 6.1
Explore 11 Videos
- MISCELLANEOUS VOLUME 2Book:CENGAGE PHYSICSChapter:MISCELLANEOUS VOLUME 2Exercise:INTEGER_TYPE
Explore 10 Videos
- NEWTON'S LAWS OF MOTION 2Book:CENGAGE PHYSICSChapter:NEWTON'S LAWS OF MOTION 2Exercise:Integer type
Explore 1 Video
Similar Questions
In the Fig. shown, mass 'm' is being pulled on the incline of a wedge of mass M. All the surface are smooth. Find the acceleration of the wedge.
View SolutionAssuming all the surfaces to be smooth, find the acceleration of the triangular block of mass M when the block of mass m slides on it.

View Solution
Knowledge Check
All surfaces are smooth. The acceleration of mass m relative to the wedge is
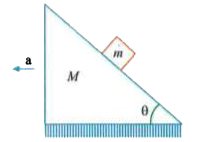 AgsinθBgsinθ+acosθCgsinθ−acosθDacosθ
AgsinθBgsinθ+acosθCgsinθ−acosθDacosθAll surfaces are smooth The acceleration of mass m relative to the wedge is
 .AgsinθBgsinθ+acosθCgsinθ−acosθDacosθ
.AgsinθBgsinθ+acosθCgsinθ−acosθDacosθIn fig. mass m is being pulled on the incline of a wedge of mass M. All the surfaces are smooth. Find the acceleration of the wedge.
 Aa=F(1−cosθ)mg2sinθcosθM+2msin2θBa=F(1+cosθ)+mgsinθcosθM+msin2θCa=F(1−cosθ)−mgsinθcosθM+msin2θDa=F(1+cosθ)−mgsinθcosθM−msin2θ
Aa=F(1−cosθ)mg2sinθcosθM+2msin2θBa=F(1+cosθ)+mgsinθcosθM+msin2θCa=F(1−cosθ)−mgsinθcosθM+msin2θDa=F(1+cosθ)−mgsinθcosθM−msin2θ
A block of mass m1=2 kg is kept on a smooth horizontal table. Another block of mass m2=1 kg is connected to m1 by a light inextensible string passing over a smooth pulley as shown in the figure. If the blocks are released, what will be the (a) acceleration of each block (b) tension in the string?
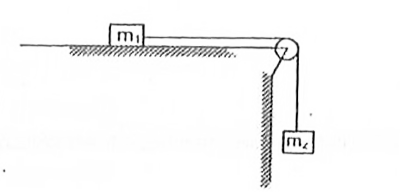
View SolutionTwo block of masses m1 and m2 are in equilibrium. The block m2 hangs from a fixed smooth pulley by an inextensible string that is fitted with a light spring of stiffness k as shown in fig. Neglecting friction and mass of the string, find the acceleration of the bodies just after the string S is cut.

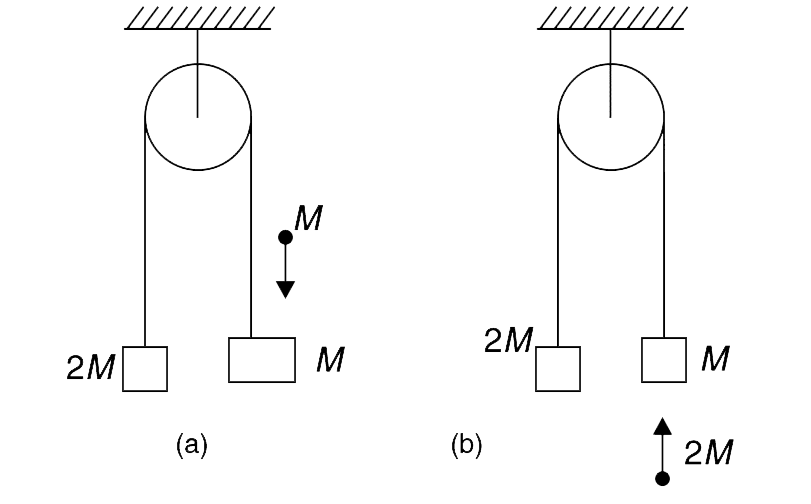
View SolutionTwo blocks of mass M and 2M are connected to the two ends of a light, inextensible string passing over an ideal pulley as shown in figure. The system is released from rest.
(a) One second after the system is released, a particle of mass M hits the block of mass M and sticks to it. The particle hits the block with a speed of 10 m/s while travelling downward. Find the total distance travelled by block of mass 2M after it is released.
(b) One second after the system is released, a particle of mass 2M hits the block of mass M and sticks to it. The particle hits the block with a speed of 10 m/s while travelling in upward direction. Find distance travelled by the block of mass 2M after it is released to the time it comes to rest for the first time (g=10m/s)2
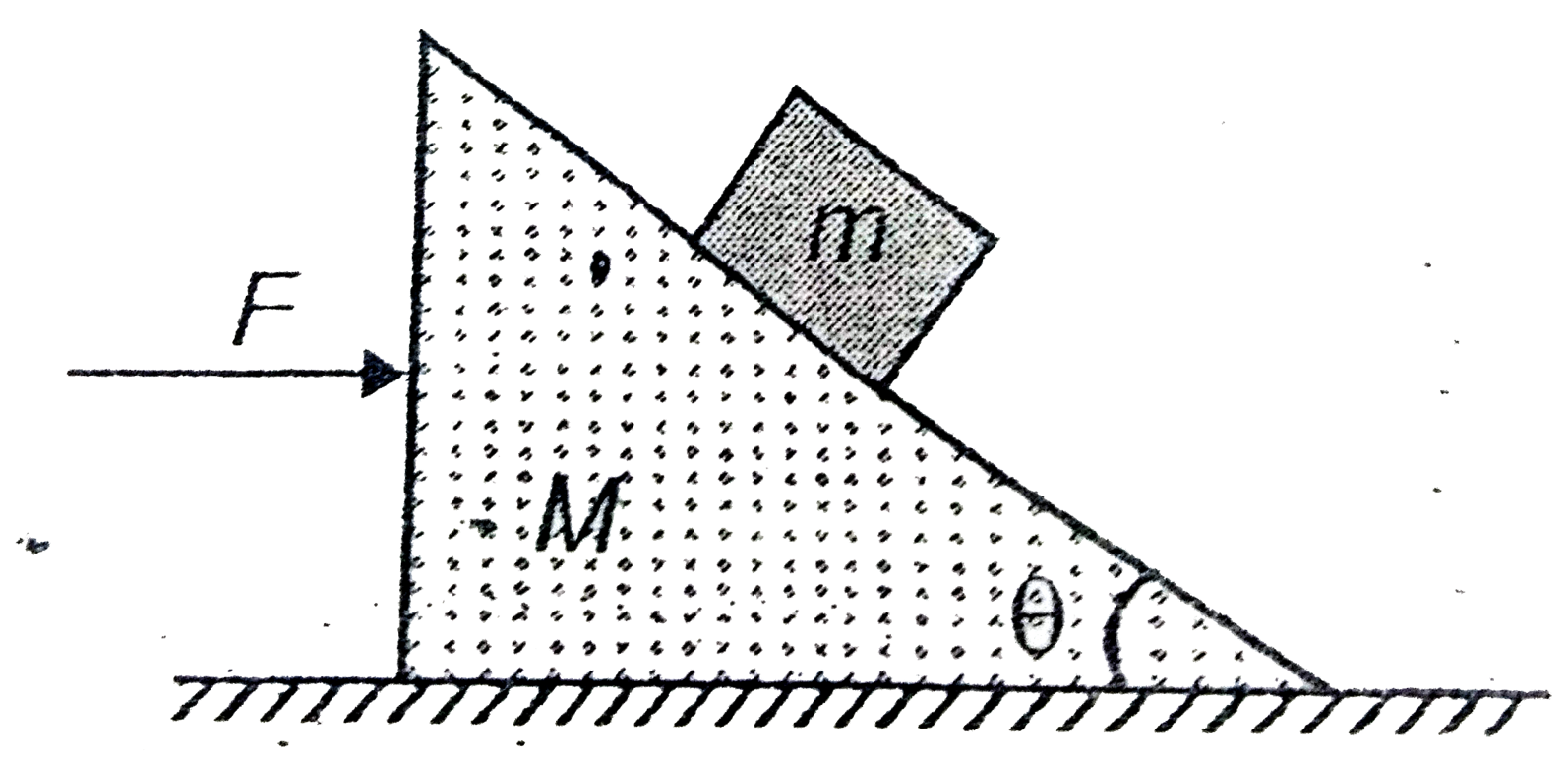
View SolutionA block of mass m is placed on a wedge of mass M and a force F is acting on its as shown . If all surfaces are smooth , find the force F such that, there is no relative motion between m and M.
View SolutionAll the surfaces are smooth as shown in figure. The acceleration of mass m relative to wedge is :

View Solution

