A block of mass m is placed on the inclined sufrace of a wedge as shown in fig. Calculate the acceleration of the wedge and the block when the block is released. Assume all surfaces are frictionless.

Method 1: Analysis form ground frame: Let the acceleration of wedge be A and that of block be a (w.r.t wedge).
Then, acceleration of m w.r.t ground is
→am=→am,M+→aM=(acosθˆi−asinθˆj)−Aˆi
=(acosθ−A)ˆi−asinθˆj...(i)
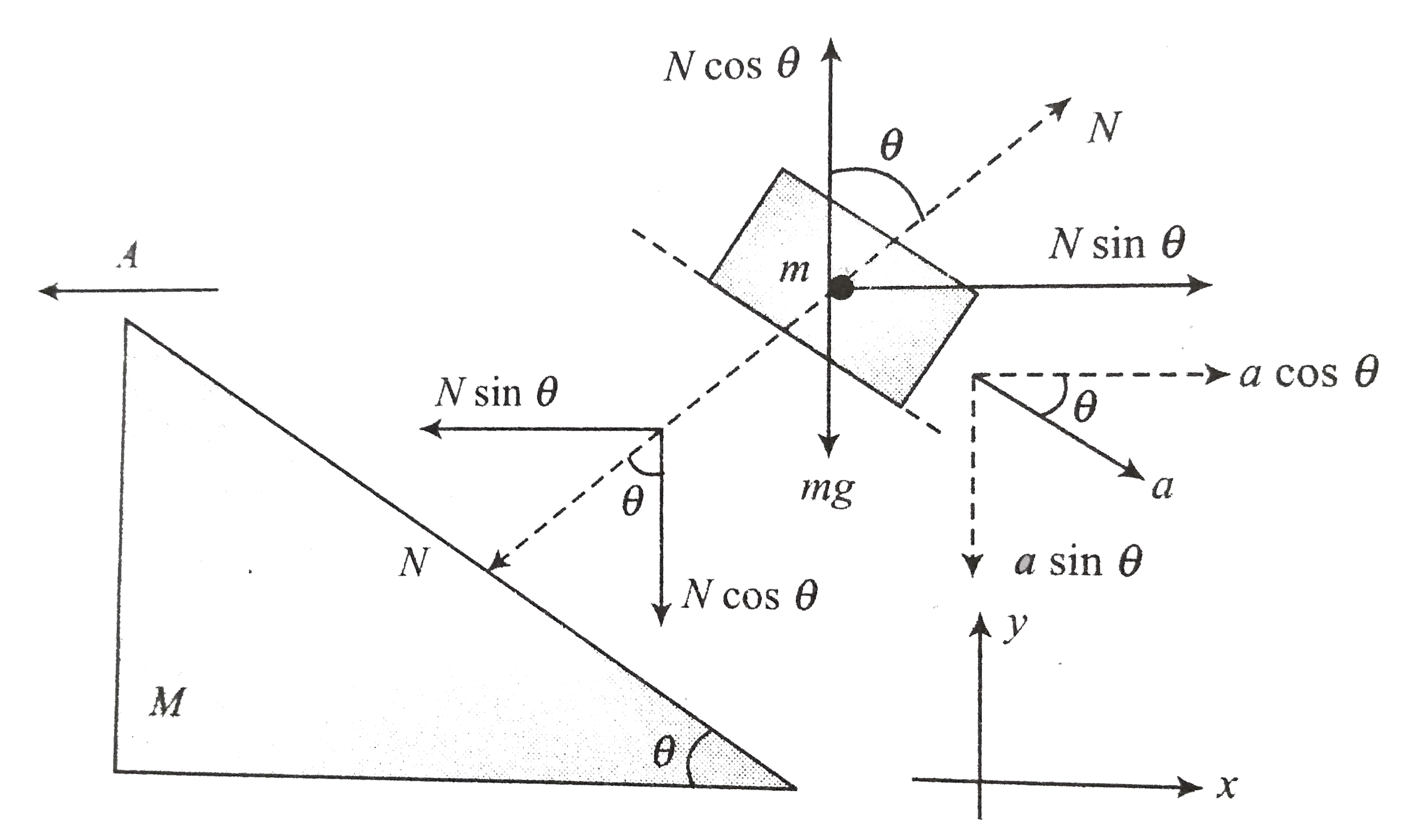
For M: Nsinθ=MA ...(ii)
For m: mg−Ncosθ=masinθ ...(iii)
Nsinθ=m(acosθ−A)...(iv)
Solve (ii), (iii) and (iv) to get
A=mgsinθcosθM+msin2θ and (M+m)gsinθM+msin2θ
Now acceleration of block can be found by putting the values of a in (i)
Method 2: If we consider the motion of block parallel and perpendicular to sloping surface w.r.t. ground, acceleration of m can also be written as :
→am=→am,M_→aM=−aˆi+(Acosθˆi+Asinθˆj)

→am=(Acosθ−a)ˆi+Asinθˆj ...(v)
For M: Nsinθ=MA ...(vi)
For m: −mgsinθ=m(Acosθ−a) ...(vii)
mgcosθ−N=mAsinθ ...(viii)
From above equation we can get the valuve of
A=mgsinθcosθM+msin2θ and (M+m)gsinθM+msin2θ
Method 3: Analysis from non-inertial frame: With the help of pseudo force. If we consider the motion of block parallel and perpendicular to ground.

let us make teh FBD of m w.r.t. M.
For M: Nsinθ=MA...(ix)
For m: Nsinθ+mA=macosθ ...(x)
mg−Ncosθ=masinθ ...(xi)
From above equations, we can get the value of
A=mgsinθcosθM+msin2θ and (M+m)gsinθM+msin2θ
Method 4: Analyses from non-inertial frame: With the help of pseudo force.

When the forces are resolved in directions along the plane and perpendicular to the plene:
For M: Nsinθ=MA
for m: mgsinθ+mAcosθ=ma
mgcosθ=N+mAsinθ
From above equations, we can get the value of
A=mgsinθcosθM+msin2θ and (M+m)gsinθM+msin2θ
Method 5: Taking system together:
Considering wedge and block together as a system as shown in fig.

When the system is released, the wedge will start moving towards left with acceleration A and the block will starts sliding on the sloping surface of the wedge with acceleration a with respects to wedge as shown in fig.
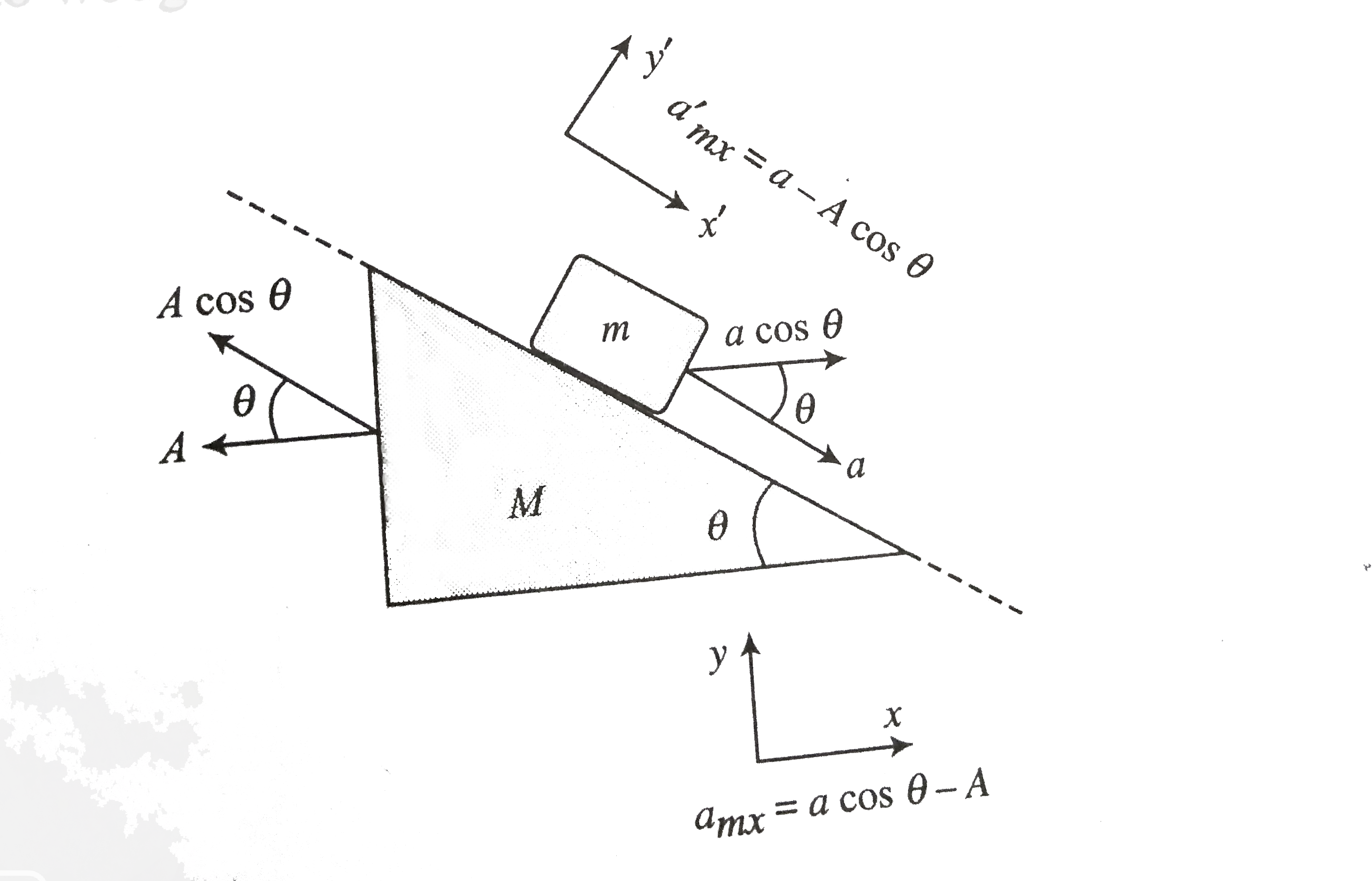
Now analyzing the system in the horizontal directon, the system is not having any external force in horizontal direction. So we can apply
Σ→Fx=Σmi→ai=m→am+M→aM
Σ→Fx=0⇒−MA+m(acosθ−A)=0
⇒a=(m+M)Amcosθ ..(i)
Now considering the motion of block parallel to the sloping side. Writing the equation of motion with respect to ground.
Σ→Fx'=Σm→ax'
⇒mgsinθ=ma'x
=m(a−Acosθ) ...(ii)
Solve (i) and (ii) to get
A=mgsinθcosθM+msin2θ and (M+m)gsinθM+msin2θ
Topper's Solved these Questions
- NEWTON'S LAWS OF MOTION 1Book:CENGAGE PHYSICSChapter:NEWTON'S LAWS OF MOTION 1Exercise:Exercise 6.1
Explore 11 Videos
- NEWTON'S LAWS OF MOTION 1Book:CENGAGE PHYSICSChapter:NEWTON'S LAWS OF MOTION 1Exercise:Exercise 6.2
Explore 35 Videos
- NEWTON'S LAWS OF MOTION 1Book:CENGAGE PHYSICSChapter:NEWTON'S LAWS OF MOTION 1Exercise:Integer
Explore 5 Videos
- MISCELLANEOUS VOLUME 2Book:CENGAGE PHYSICSChapter:MISCELLANEOUS VOLUME 2Exercise:INTEGER_TYPE
Explore 10 Videos
- NEWTON'S LAWS OF MOTION 2Book:CENGAGE PHYSICSChapter:NEWTON'S LAWS OF MOTION 2Exercise:Integer type
Explore 1 Video
Similar Questions
A block of mass m is initially lying on a wedge of mass M with an angle of inclination θ as shown in figure. Calculate the displacement of the wedge when the block is released and reaches to the bottom of the wedge.

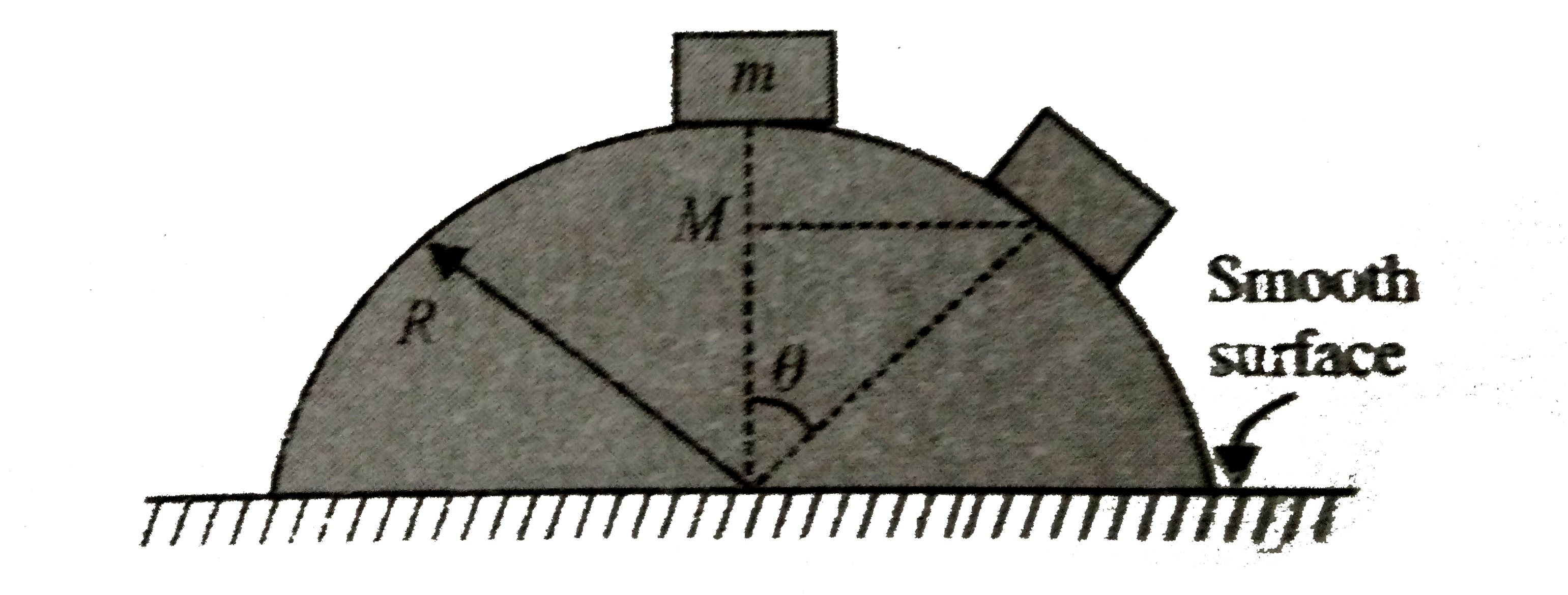
View SolutionA block is released on the convex surface of a hemispherical wedge as shown in Fig. Determine the displacement of the wedge when the block reaches the angular position θ
View Solution
Knowledge Check
In fig. mass m is being pulled on the incline of a wedge of mass M. All the surfaces are smooth. Find the acceleration of the wedge.
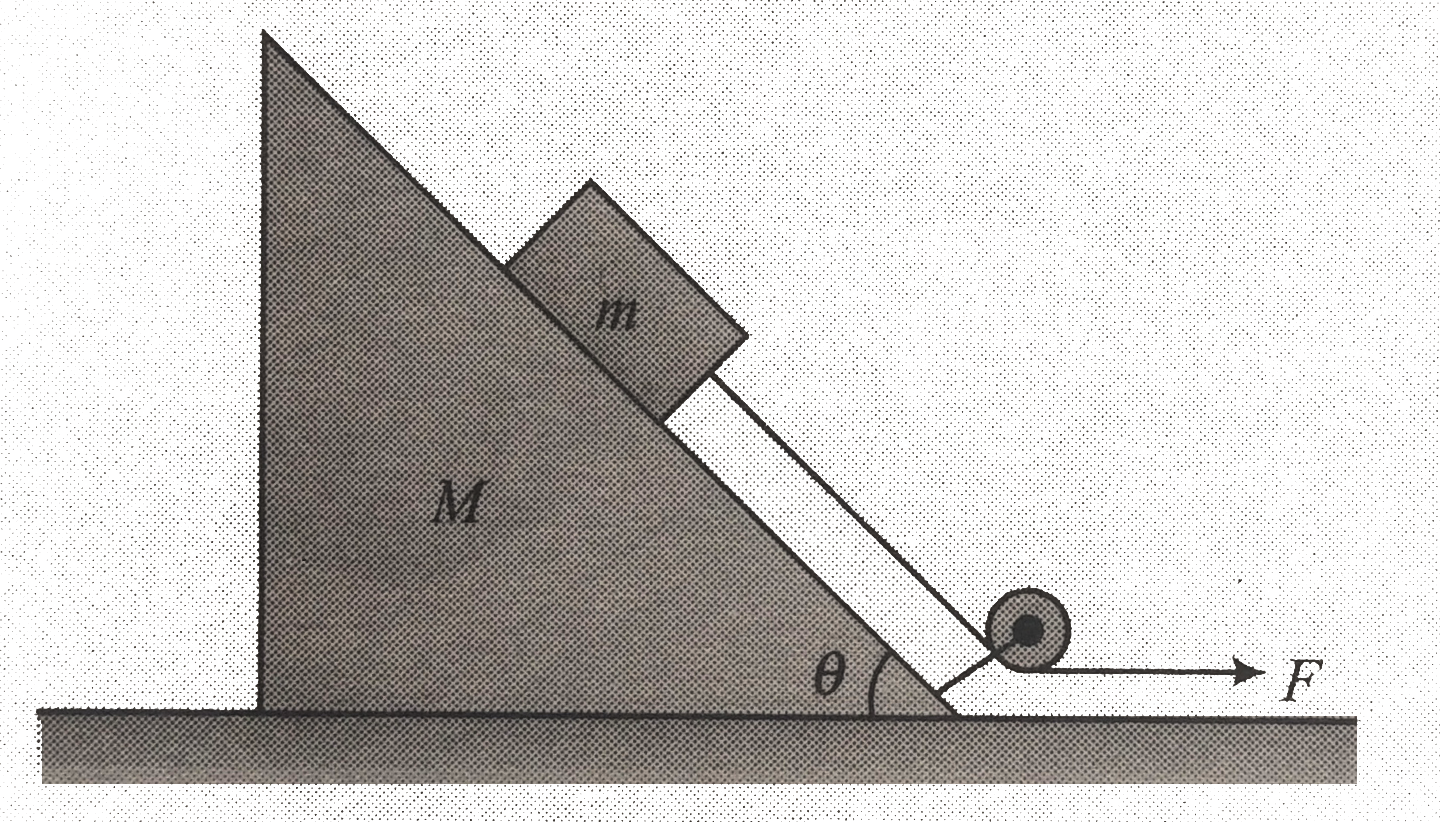 Aa=F(1−cosθ)mg2sinθcosθM+2msin2θBa=F(1+cosθ)+mgsinθcosθM+msin2θCa=F(1−cosθ)−mgsinθcosθM+msin2θDa=F(1+cosθ)−mgsinθcosθM−msin2θ
Aa=F(1−cosθ)mg2sinθcosθM+2msin2θBa=F(1+cosθ)+mgsinθcosθM+msin2θCa=F(1−cosθ)−mgsinθcosθM+msin2θDa=F(1+cosθ)−mgsinθcosθM−msin2θA block of mass 1 kg is placed on a wedge shown in figure. Find out minimum coefficient of friction between wedge and block to stop the block on it.
 A0.6B0.9C1D0.2
A0.6B0.9C1D0.2
A block of mass m is at rest on a rought wedge as shown in figure. What is the force exerted by the wedge on the block?

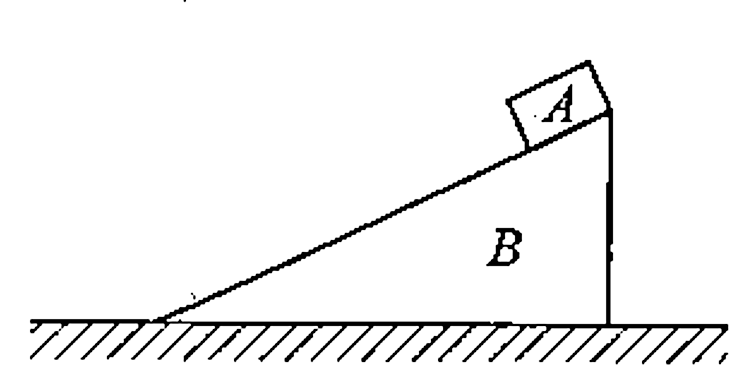
View SolutionA block A (mass 4M) is placed on the top of a wedge block B of base length l (mass=20M) as shown in figure. When the system is released from rest. Find the distance moved by the block B till the block A reaches ground Assume all surfaces are frictionless.
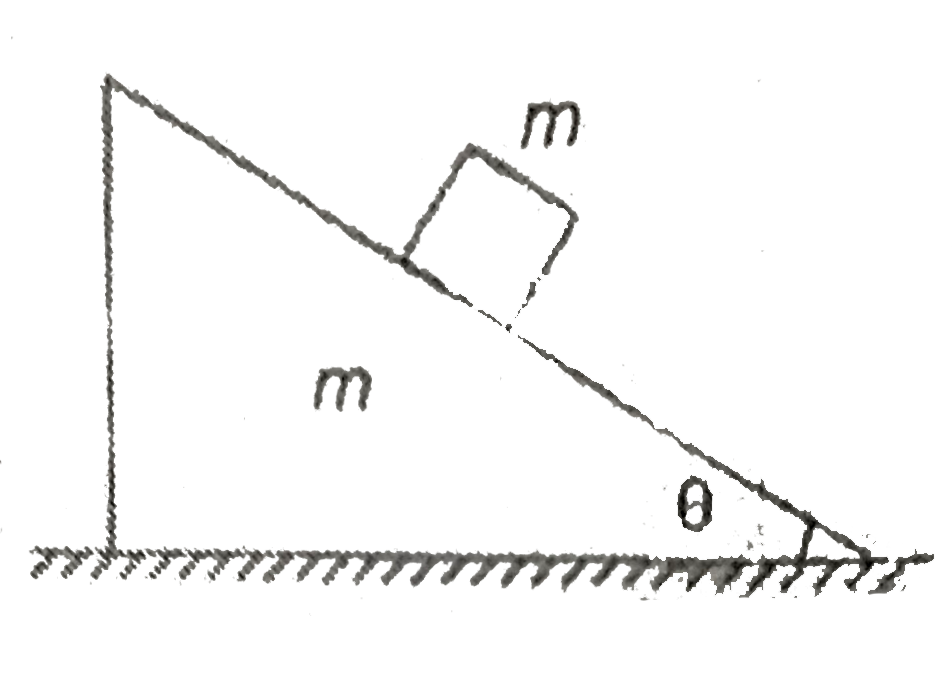
View SolutionA block of mass m slides down on inclined wedge of same mass m as shown in figure . Friction is absent everywhere . Acceleration of centre of mass of the block and wedge is
View SolutionA wedge of mass M makes an angle θ with the horizontal. The wedge is placed on horizontal frictionless surface. A small block of mass m is placed on the inclined surface of wedge. What horizontal force F must be applied to the wedge so that the force of friction between the block and wedge is zero ?
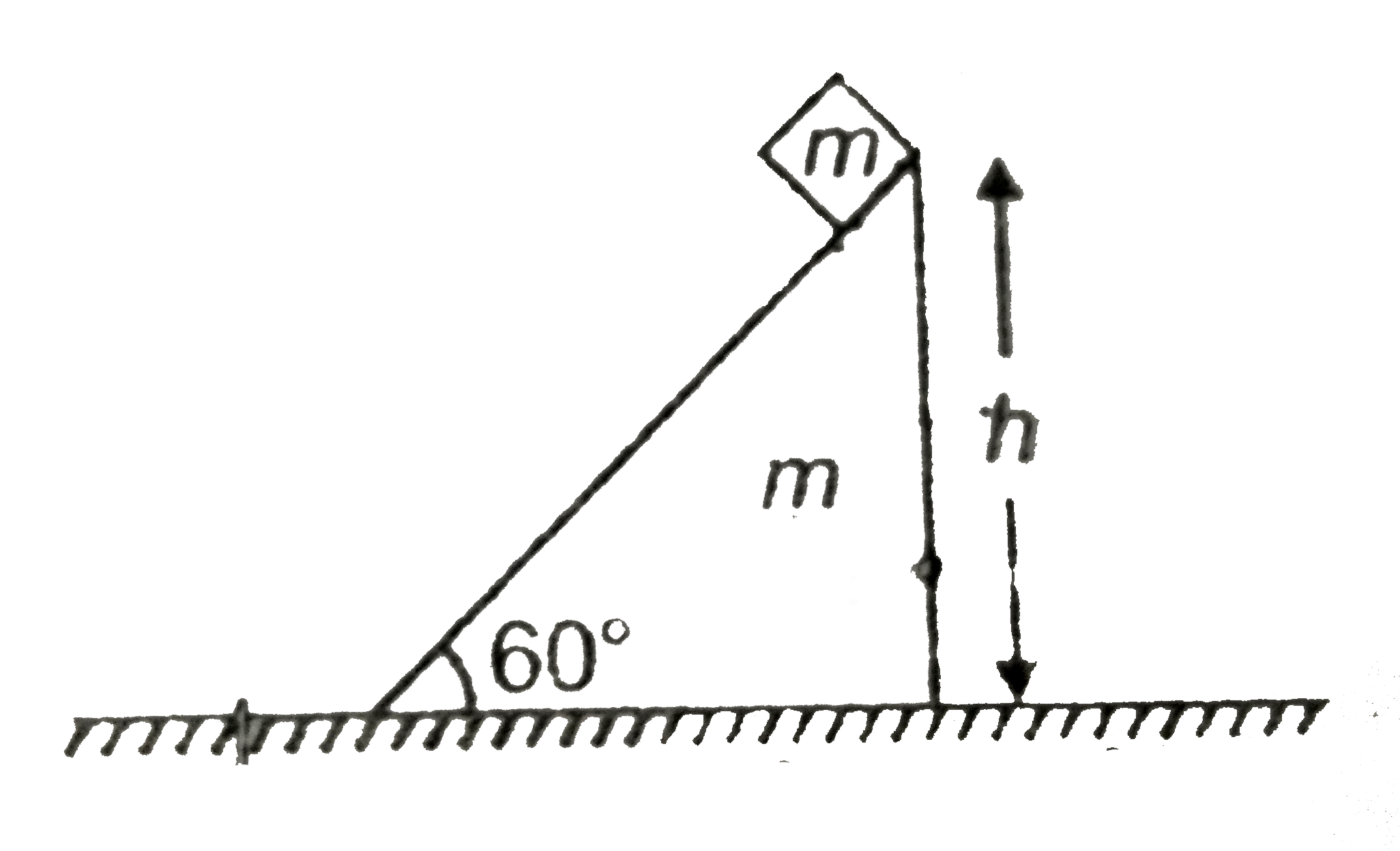
View SolutionA block of mass m is released from a wedge of mass m as shown in figure . Find the time taken by the block to reach the end of the wedge.
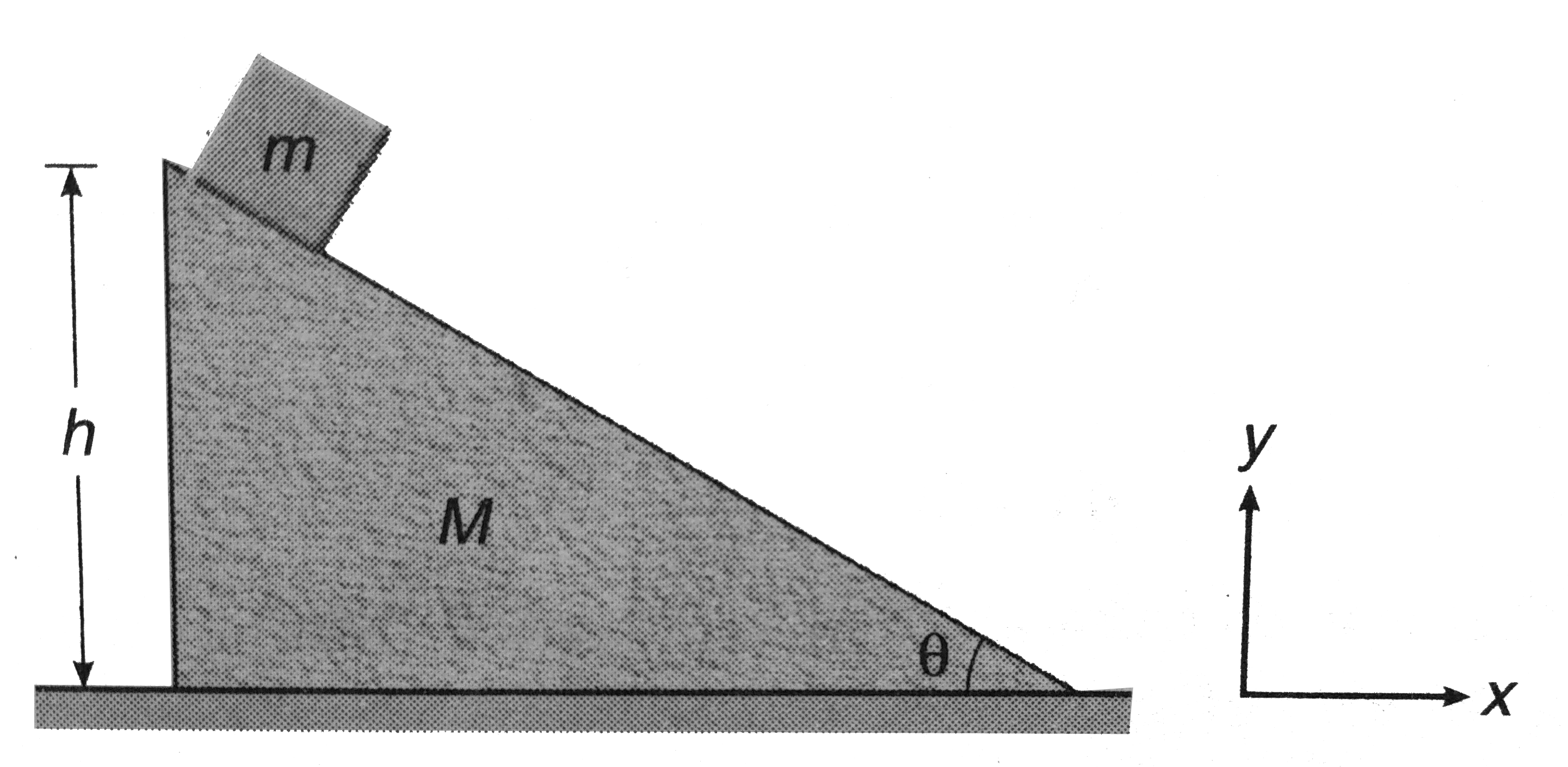
View SolutionA block of mass m is released from the top of a wedge of mass M as shown in figure. Find the displacement of wedges on the horizontal ground when the block reaches the bottom of the wedges. Neglect friction everywhere.
View Solution

