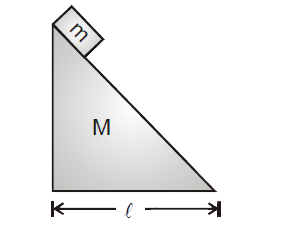
A block of mass m is initially lying on a wedge of mass M with an angle of inclination θ as shown in figure. Calculate the displacement of the wedge when the block is released and reaches to the bottom of the wedge.

l=hcosθ
Let displacement of wedge be x towards right,
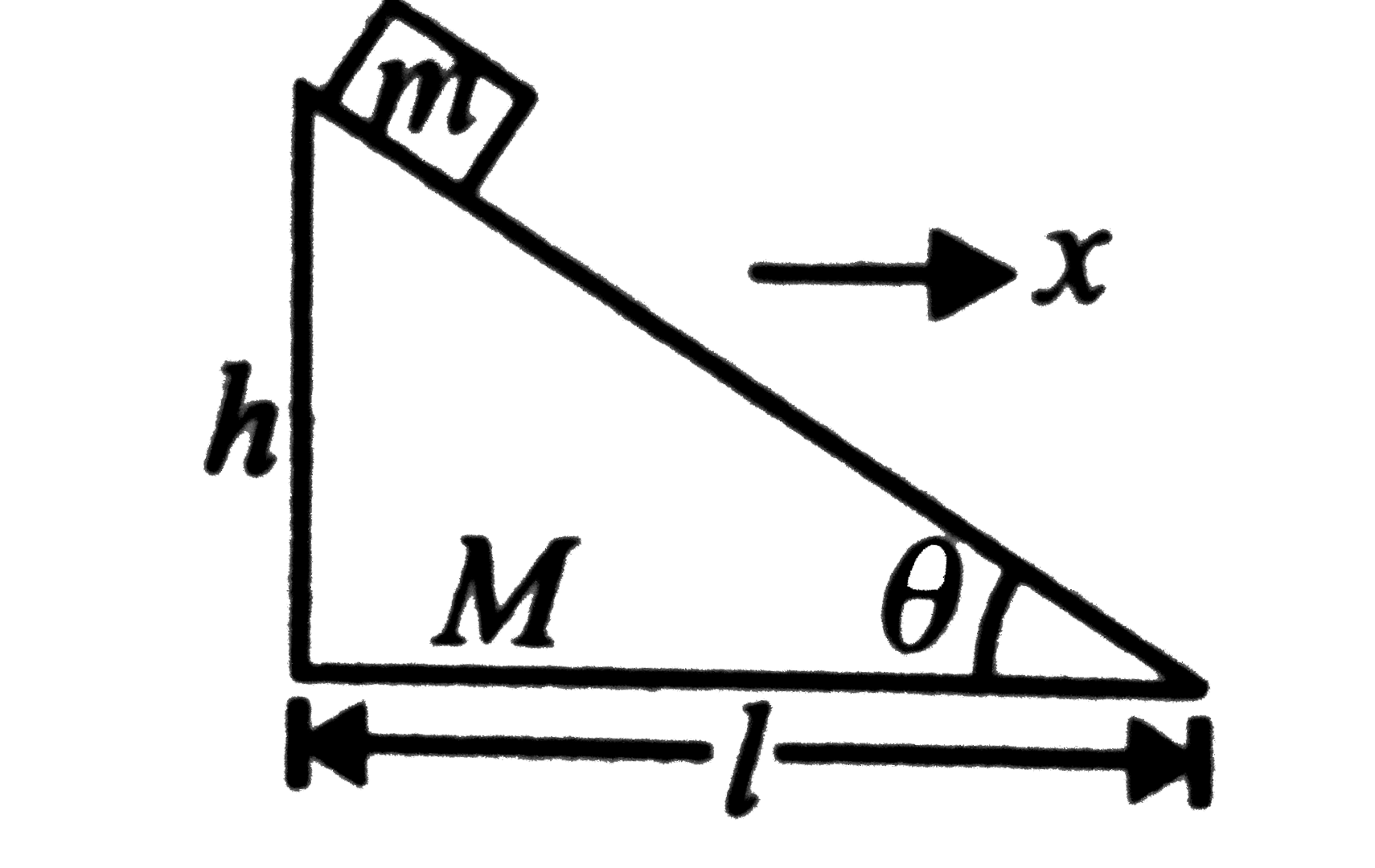
△xCM=m(1+x)+MxM+m
0=ml+(M+m)x
x=−mlM+m=mhcotθM+m
Topper's Solved these Questions
- CENTRE OF MASSBook:CENGAGE PHYSICSChapter:CENTRE OF MASSExercise:Exercise 1.2
Explore 23 Videos
- CENTRE OF MASSBook:CENGAGE PHYSICSChapter:CENTRE OF MASSExercise:Exercise 1.3
Explore 24 Videos
- CENTRE OF MASSBook:CENGAGE PHYSICSChapter:CENTRE OF MASSExercise:Solved Examples
Explore 13 Videos
- CALORIMETRYBook:CENGAGE PHYSICSChapter:CALORIMETRYExercise:Solved Example
Explore 13 Videos
- DIMENSIONS & MEASUREMENTBook:CENGAGE PHYSICSChapter:DIMENSIONS & MEASUREMENTExercise:Integer
Explore 2 Videos
Similar Questions
A block of mass m is placed on the inclined sufrace of a wedge as shown in fig. Calculate the acceleration of the wedge and the block when the block is released. Assume all surfaces are frictionless.

View SolutionA block is released on the convex surface of a hemispherical wedge as shown in Fig. Determine the displacement of the wedge when the block reaches the angular position θ
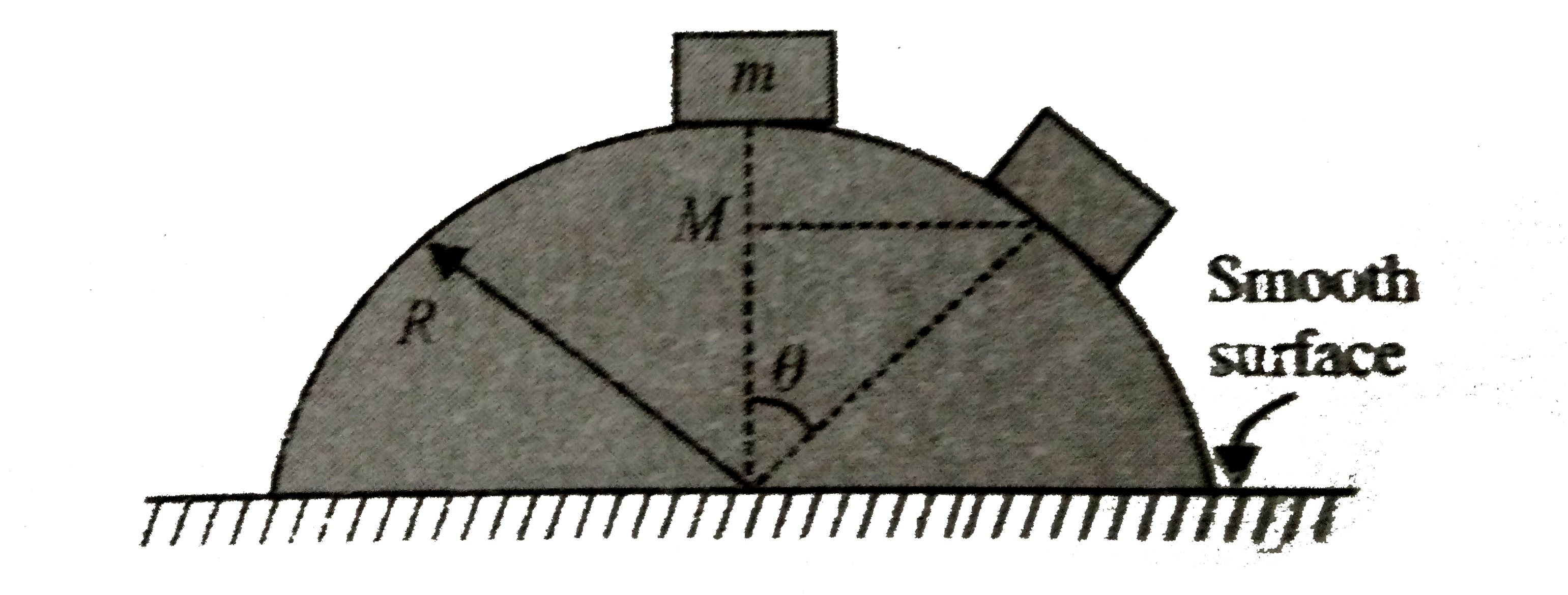
View Solution
Knowledge Check
A smooth block of mass m is held stationary on a smooth wedge of mass M and inclination θ as shown in figure .If the system is released from rest , then the normal reaction between the block and the wedge is
 AmgcosθBless than mgcosθCgreater than mgcosθDmay be less or greater than mgcosθ depending upon whether M is less or greater than m
AmgcosθBless than mgcosθCgreater than mgcosθDmay be less or greater than mgcosθ depending upon whether M is less or greater than mA ball of mass m is released from A inside a smooth wedge of mass m as shown in figure. What is the speed of the wedge when the ball reaches point B?
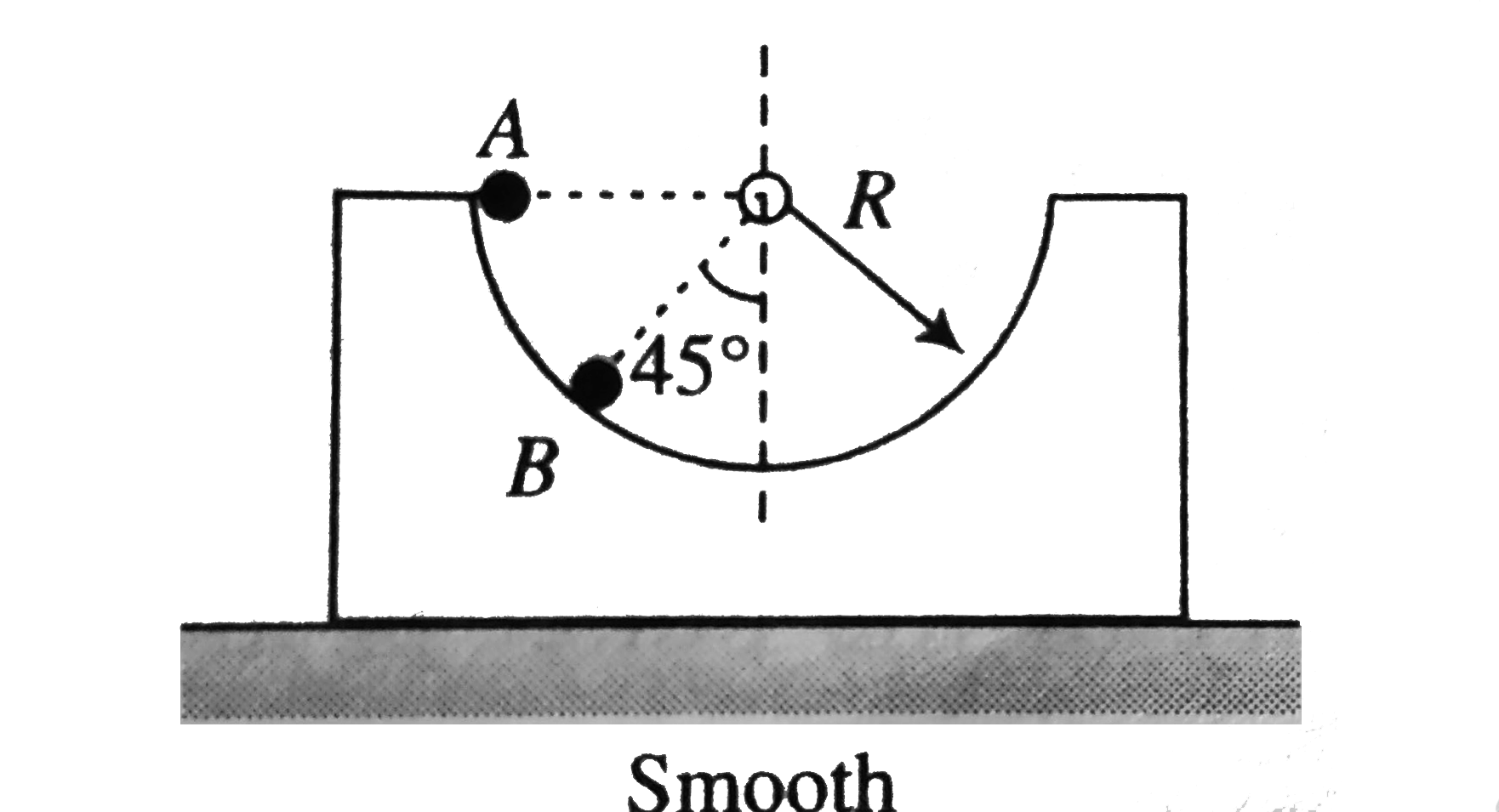 A(a) (gR3√2)1/2B(b) √2gRC(c) (5gR2√3)1/2D(d) √32gR
A(a) (gR3√2)1/2B(b) √2gRC(c) (5gR2√3)1/2D(d) √32gRA block of mass m rests on a stationary wedge of mass M. The wedge can slide freely on a smooth horizontal surface as shown in figure. If the block starts from rest
 A(a) the position of the centre of mass of the system will changeB(b) the position of centre of mass of the system will change along the vertical but not along the horizontalC(c) the total energy of the system will remain constantD(d) All of the above
A(a) the position of the centre of mass of the system will changeB(b) the position of centre of mass of the system will change along the vertical but not along the horizontalC(c) the total energy of the system will remain constantD(d) All of the above
A block of mass m is released from the top of a wedge of mass M as shown in figure. Find the displacement of wedges on the horizontal ground when the block reaches the bottom of the wedges. Neglect friction everywhere.
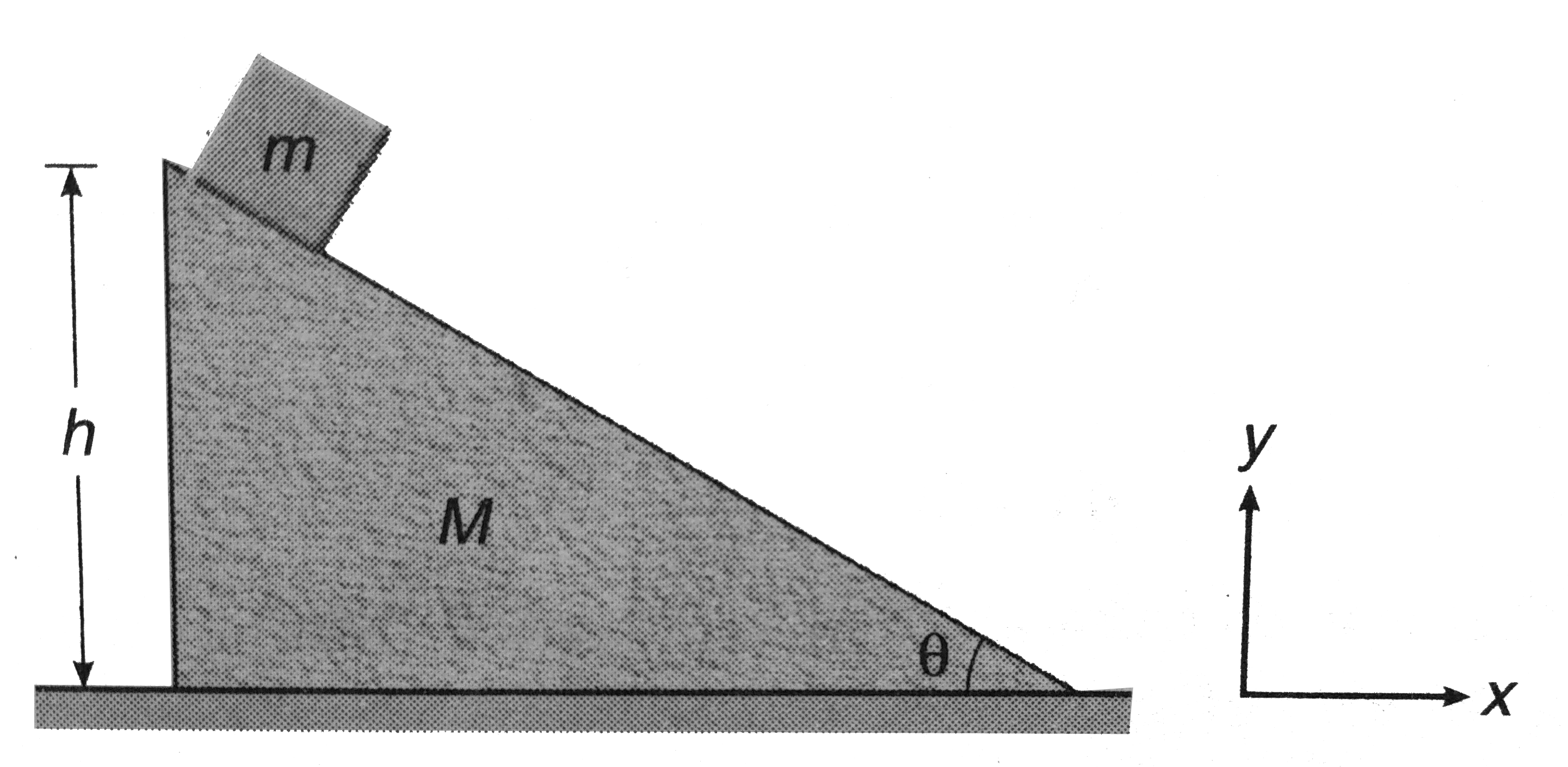
View SolutionA block of mass m is at rest on a rought wedge as shown in figure. What is the force exerted by the wedge on the block?

View SolutionA particle of mass m is placed at rest on the top of a smooth wedge of mass M, which in turn is placed at rest on a smooth horizontal surface as shown in figure. Then the distance moved by the wedge as the particle reaches the foot of the wedge is :
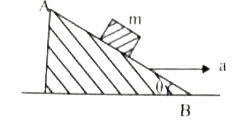
View SolutionA block of mass m is placed on a smooth inclined wedge ABC of inclination theta as shown in the figure. The wedge is given an acceleration a towards the right. The relation between a and theta for the block to remain stationary on the wedge is.

View SolutionA block of mass m is placed on a smooth inclined wedge ABC of inclination θ as shown in the figure. The wedge is given an acceleration 'a' towards the right. The relation between a and for the block to remain stationary on the wedge is:
View Solution

