Consider a system of a small body of mass m kept on a large body of mass M placed over an inclined plane of the angle of inclination θ to the horizontal. Find the acceleration of m when the system is set in motion. Assume an inclined plane to be fixed. all the contact surfaces are smooth.

Method 1: Analysis in an inertial reference frame attached to the ground :
Let a be the acceleration m w.r.t. M directed horizontally towards right.
Let A be the acceleration of M w.r.t. the ground directed along the incline downwards.

Acceleration of m w.r.t. ground will be the vector sum of the acceleration of m w.r.t. M and the acceleration of M w.r.t. ground.
force equation for m are
0=m(a−Acosθ) ..(i)
mg−N'=m(Asinθ) ...(ii)
Force equation for M are
N'sinθ+Mgsinθ=MA ...(iii)
N'cosθ+Mgcosθ−N=0 ...(iv)
from (ii),
N'=mg−mAsinθ
Subsitituting N' in (iii),
(mg−mAsinθ)sinθ+Mgsinθ=MA
⇒A=(M+m)gsinθM+msin2θ
Acceleration of m w.r.t. ground is Asinθ (since, Acosθ−a=0). Thus, the acceleration of m w.r.t. ground is
amG=Asinθ=(M+m)gsinθM+msin2θ
Method 2: Analysis of motion of m in the non-inertial reference frame attached to M:
Let the acceleration of M w.r.t ground be A along the inclined plane downwards. Consider that ground is an inertiail reference frame, the reference frame attached to M will be non-inertial . For applying Newton's second law of motion to any object w.r.t. on the object which equals mass of the objects times accelerations of M, directed opposite to A.
Force equation for m:

Let the acceleration of m w.r.t. M be a, in the horizontal direction towards right.
The force acting on m are:
∗weight of m, mg, acting vertically downwards
∗ Normal force on m by M, N' , vertically upwards, and
∗ (mA), the inertial force acting along the incline upwards, as the acceleration of M is A along the incline downwards.
N'+(mA)sinθ=mg ..(i)
(mA)cosθ=ma ..(ii)
Force equation for M:
The force acting on M are
∗ The weight Mg
∗N', normal force exerted by m
∗N, normal force exerted by the incline
Mgsinθ+N'sinθ=MA..(iii)
(Along the incline)
Mgcosθ+N'cosθ=N ...(iv)
(Perpendicular to the incline)
From (i),(iii) and (iv)
A=(M+m)gsinθM+msin2θ
Acceleration of m relative to ground.
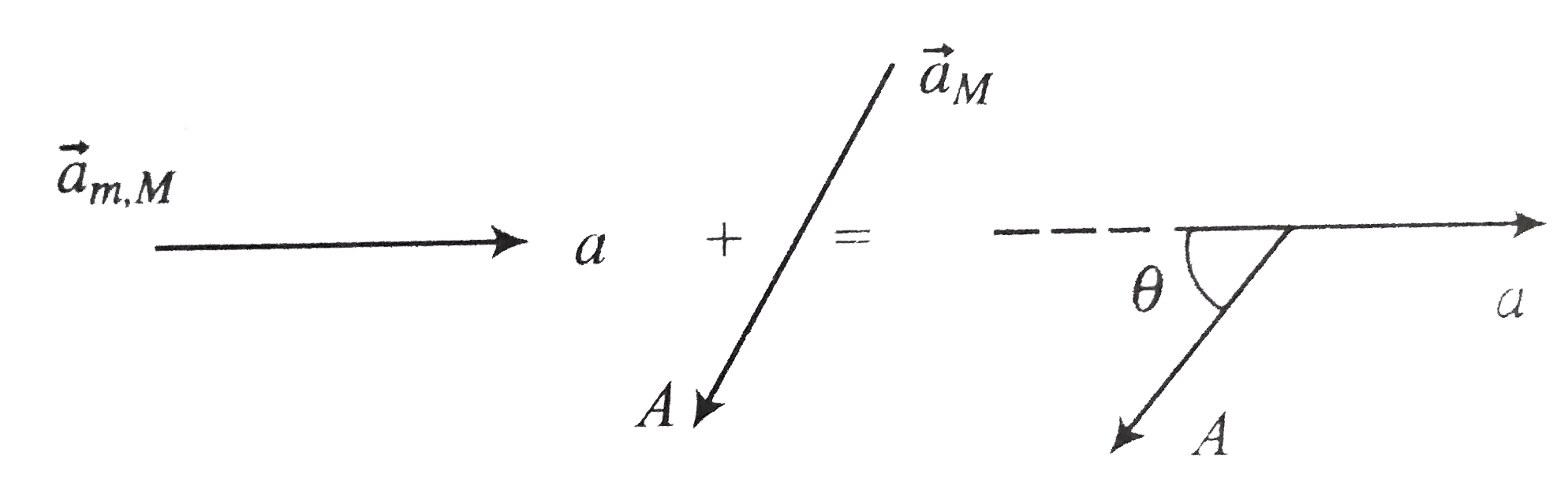
→am=→amM+→aM
=aˆi+Acosθ(−ˆi)+Asinθ(−ˆj)
But a=Acosθ [ form(ii)], therefore,
am=Asinθ, vertically downward
(M+m)gsin2θM+msin2θ
Method 3: Considering M and m as system

The system has (M+m)gsinθ external force parallel to inclined plane.
→Fx'=M(→aM)x'+m(→am)x'
(→am)x'=(→am,M)x'+(→aM)x'
=−acosθ+A=(A−acosθ)
MA+m(A−acosθ)=(M+m)gsinθ ...(i)
Considering the motion of block in horizontal direction only and writing equation of motion w.r.t. ground,
(→am)x=a−Acosθ
The block is not having any external force in horizontal direction
Σ→Fx=0=m(→am)x=m(a=Acosθ)
or a=Acosθ ...(ii)
From (i) and (ii)
MA+m[A−(Acosθ)cosθ]=(M+m)gsinθ
MA+mAsin2θ=(M+m)gsinθ
After solving, we get
A=(M+m)gsinθM+msin2θ
Topper's Solved these Questions
- NEWTON'S LAWS OF MOTION 1BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - NEWTON'S LAWS OF MOTION 1EXERCISE - Exercise 6.1
11 Videos
- NEWTON'S LAWS OF MOTION 1BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - NEWTON'S LAWS OF MOTION 1EXERCISE - Exercise 6.2
35 Videos
- NEWTON'S LAWS OF MOTION 1BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - NEWTON'S LAWS OF MOTION 1EXERCISE - Integer
5 Videos
- MISCELLANEOUS VOLUME 2BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - MISCELLANEOUS VOLUME 2EXERCISE - INTEGER_TYPE
10 Videos
- NEWTON'S LAWS OF MOTION 2BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - NEWTON'S LAWS OF MOTION 2EXERCISE - Integer type
1 Videos
Similar Questions
A solid sphere of mass m rolls without slipping on an inclined plane of inclination θ. The linear acceleration of the sphere is
View SolutionA block of mass m is placed on a smooth inclined plane of inclination θ with the horizontal. The force exerted by the plane on the block has a magnitude
View SolutionA block of mass m is placed on a smooth inclined plane of inclination θ with the horizontal. The force exerted by the plane on the block has a magnitude
View SolutionA block of mass m is kept on an inclined plane is angle inclination θ(<ϕ), where ϕ= angle of friction. Then :

View SolutionA body of mass m is kept on a rough fixed inclined plane of angle of inclination θ=30∘. It remains stationary. Then magnitude of force acting on the body by the inclined plane is equal to :
View SolutionA body is placed on a smooth inclined plane of inclination 1 in x. The horizontal acceleration to be given to the inclined plane so that the body on it remains at rest with respect to inclined plane is
View SolutionA block of mass m is placed at rest on an inclination θ to the horizontal. If the coefficient of friction between the block and the plane is μ, then the total force the inclined plane exerts on the block is
View SolutionA block is placed on a smooth inclined plane at an angle 'θ' to the horizontal. The acceleration must the plane be moved horizontally so that the block to fall freely is
View SolutionIn fig. mass m is being pulled on the incline of a wedge of mass M. All the surfaces are smooth. Find the acceleration of the wedge.

View SolutionA block is kept on a smooth inclined plane of angle of inclination θ that moves wuth a contact acceleration so that the block does not slide relative to the inclined plane. If the inclined plane stops the normal contact force offered by the plane on the block changes by a factor
View Solution
